软件滤波的示波血压测量算法及Android实现

许永峰， 贺玉成， 周林

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021;2. 厦门市移动多媒体通信重点实验室， 福建 厦门 361021)

软件滤波的示波血压测量算法及Android实现

许永峰1,2， 贺玉成1,2， 周林1,2

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021;2. 厦门市移动多媒体通信重点实验室， 福建 厦门 361021)

提出软件滤波与示波法相结合的改进算法.利用三重软件滤波处理，针对传统示波法血压测量中脉搏振荡波提取和波形突变点选择的困难，从混合压力信号采样数据中有效提取出特征明显的脉搏振荡波，通过幅度系数法确定脉搏振荡波中突变点的幅值范围，利用波形判别法仅在该幅值范围内选取突变点，完成舒张压和收缩压的测量.在Matlab中进行仿真，并在Android移动平台上实现.Matlab仿真结果表明：该算法具有较强的可靠性和准确性. 关键词： 血压测量； Android； 示波法； 软件滤波

血压是反应人体生理状态的一个重要参数.大量调查表明，采用便携式电子血压计进行日常血压监护，是预防心血管等疾病的重要手段之一[1].临床上血压测量主要包括直接法和间接法.直接测量法的测量精确度高，但有一定的创伤性，不适合日常测量.间接法主要包括柯式音法和示波法[2-3]等.相比于有创法，无创测量方法具有安全、方便等特点，在临床上得到广泛的应用.李雪情等[3]通过确定振荡波包络线的最佳拟合曲线，寻找包络线的最大值，并以积分公式确定舒张压和收缩压的位置.侯功等[4]将幅度系数法和波形特征法结合起来，提高了血压测量的准确性.王维维等[5]采用简单的非线性形态滤波器，得到脉搏振荡波，并结合波形特征法和S判决法实现血压测量.本文提出软件滤波与示波法相结合的血压测量算法.

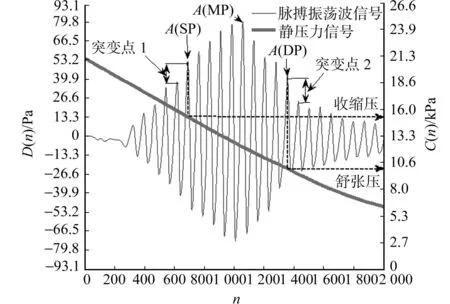
图1 基于脉搏振荡波的示波法的血压测量原理Fig.1 Blood pressure measuring principle of oscillometric method based on oscillation wave

1 示波法血压测量原理

示波法主要基于袖带内气体振动波的变化，对振荡波进行检测和分析，获得收缩压和舒张压等生理参数[2].最常用的示波法血压测量法可分为两类：幅度系数法和波形特征法[2-4].示波法已经成为便携式血压计中最流行的测量方法之一[3-6].MATLAB仿真过程中所获得的经过滤波处理的脉搏振荡波采样图，如图1所示.图1中：n为采样序号；D(n)为振荡波幅值；C(n)为静压力值.

幅度系数法通过识别振荡波的最大幅度来确定收缩压和舒张压[3-4].令A(MP)为振荡波的最大波幅，其对应的静压力即为平均压[6]；令A(SP)和A(DP)分别表示收缩压和舒张压所在波峰的幅度值，其对应的静压力分别为收缩压和舒张压.A(SP)和A(DP)的位置将分别由下述比例关系确定，即

(1)

(2)

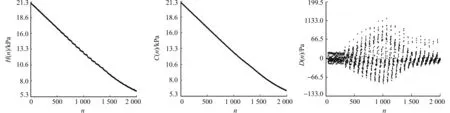
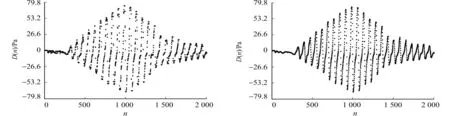
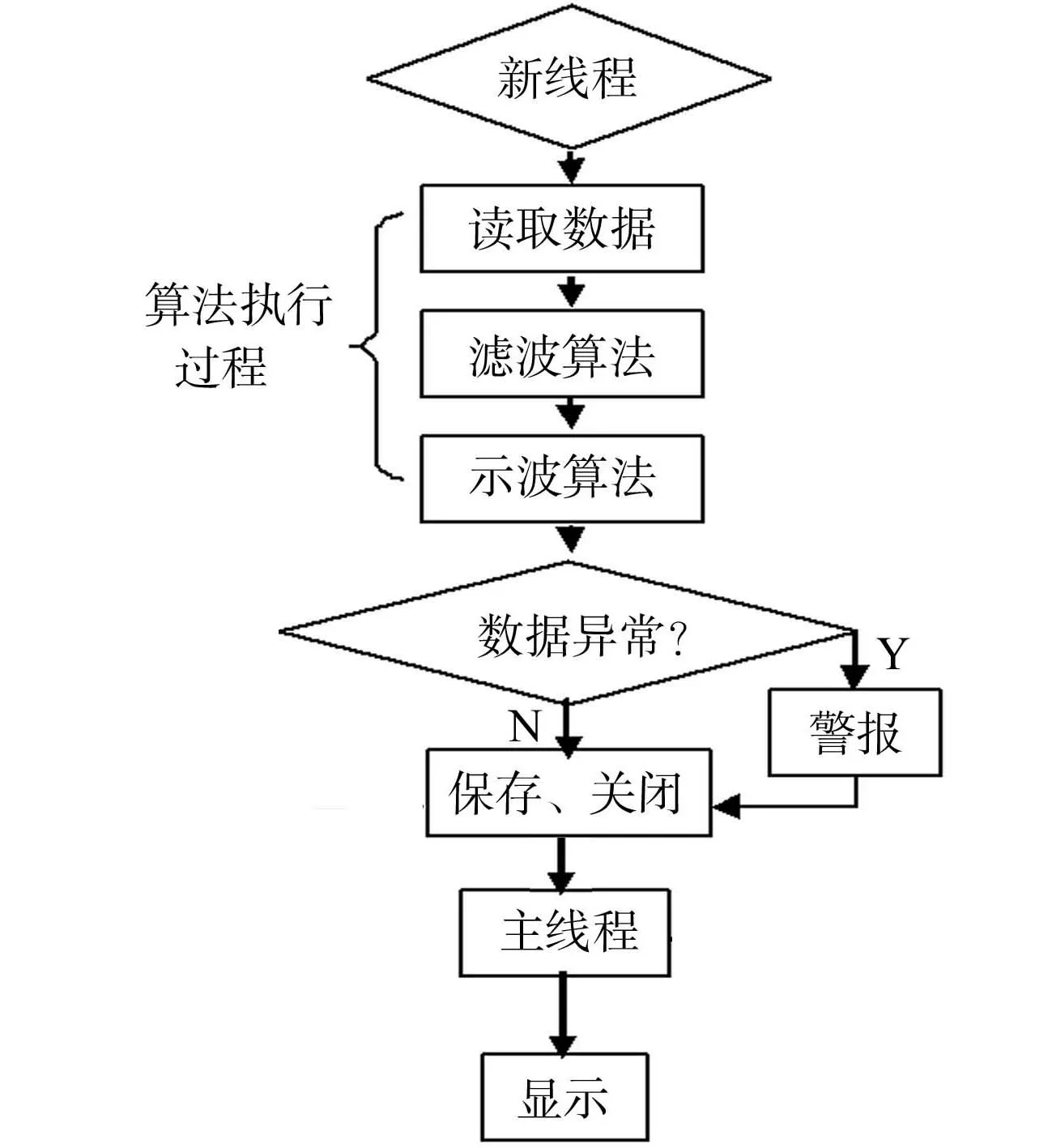
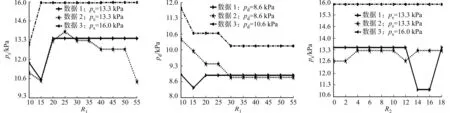
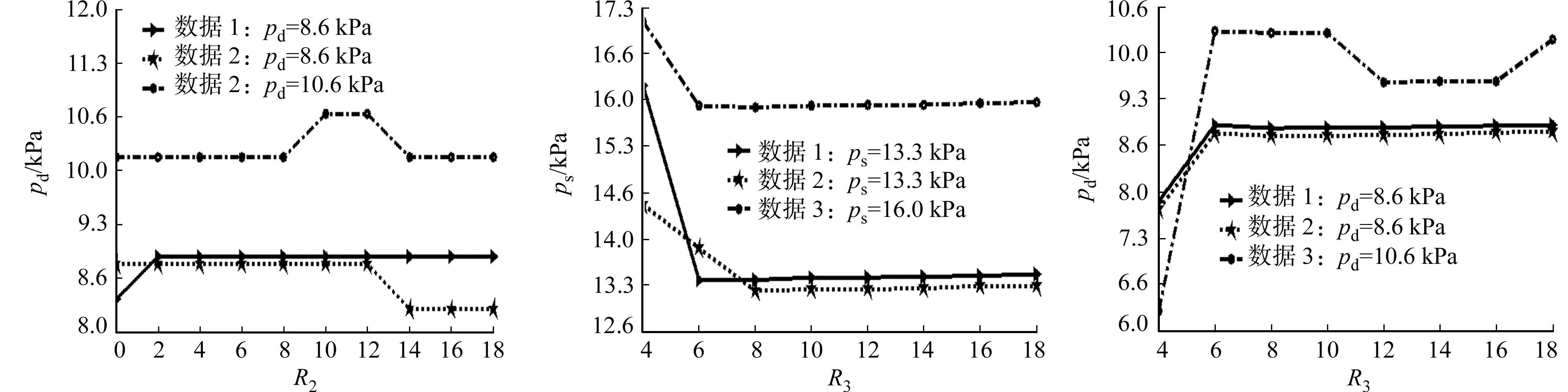
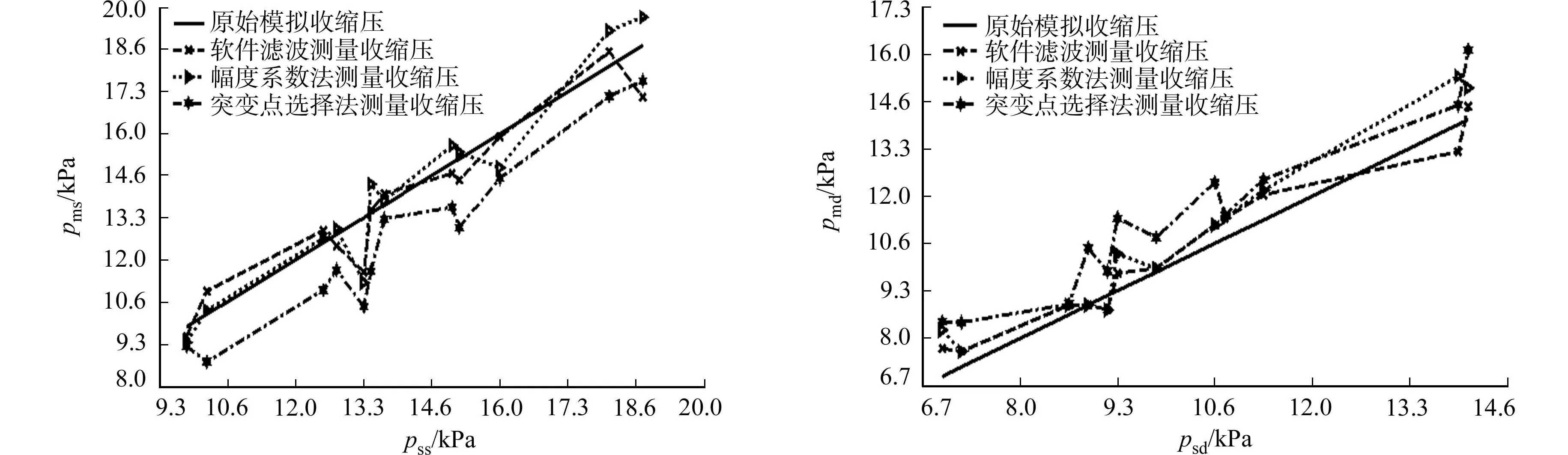
式(1)～(2)中:x1和x2称为幅度系数，取值范围为0.3

波形特征法通过识别振荡波的波形特征确定收缩压和舒张压[3-4].波形特征法认为收缩压和舒张压对应的波峰幅度值将发生较大的突变.最大波幅A(MP)左边最大差值对应的左波峰点为收缩压的位置(图1中突变点1)；最大波幅A(MP)右边最大差值对应的右波峰点为舒张压的位置(图1中突变点2).波形特征法的缺点是容易受外界干扰而缺乏稳定的测量精度[3-4].

2 血压测量算法设计

血压测量中，首先，需要从混合压力信号中提取出脉搏振荡波；然后，用一定的血压判定准则对脉搏振荡波进行特征分析.因此，文中考虑采用软件滤波器实现混合压力信号的处理.软件滤波法因节省了硬件设计、具备可移植性强等优点，而得到了广泛地应用[7].

2.1 软件滤波算法

适合血压测量的滤波算法主要包括均值滤波和中值滤波，它们常用于去除图像噪声.

均值滤波主要采用邻域平均法，就是针对每一个当前待处理数据点，根据预先设定的模板，对该数据点周围位于模板中的所有邻域数据求取算术平均值，再把该均值赋予当前数据点.用公式可表述为

(3)

式(3)中：xi为模板中邻近数据点的值；R为模板的半径，即滤波半径.

中值滤波是一种基于排序统计理论的非线性信号处理技术，能够有效地抑制噪声.其实现原理也是基于预先设定的模板，将信号中某个数据的邻域数据按大小进行排序，然后，选择该序列的中间值替代当前数据，从而消除孤立的噪声点.其排序公式为

(4)

式(4)中：x1

混合压力信号包括静压力信号、振荡波信号以及外界干扰信号.其中,振荡波信号和干扰信号相对于静压力信号来说很小.因此，为了从混合信号中提取静压力信号，将振荡波信号和干扰信号当作噪声，对混合信号采用均值滤波算法进行顺滑处理，即可得到标准的静压力信号.

混合压力信号和经均值滤波处理的标准静压力信号，分别如图2，3所示.将混合信号与标准静压力信号相减，即可提取出含有噪声的振荡波信号，如图4所示.再经过中值滤波处理，即可去除振荡波所含随机噪声，如图5(a)所示.图2～5中：n表示采样序号；H(n)表示混合压力信号幅值；D(n)为振荡波幅值；C(n)为静压力值.

图2 混合压力信号的采样数据 图3 标准静压力信号 图4 带噪的振荡波信号 Fig.2 Mixed pressure Fig.3 Standard Fig.4 Oscillation wave signal sampling data pressure signal signal with noise

(a) 中值滤波后 (b) 二次均值滤波后图5 中值滤波后和二次均值滤波后的脉搏振荡波信号Fig.5 Pulse oscillation wave signal after median filtering and second mean filter

由图5(a)可知：振荡波在去噪后，其峰值点会被削平，不利于波形特征分析.因此，又引入一次均值滤波处理，以改善振荡波波形的顺滑度，最后，获得具有明显波形特征的纯净脉搏振荡波，如图5(b)所示.经过三重滤波处理得到的振荡波，有利于应用示波法确定收缩压和舒张压的突变点.

2.2 突变点选择算法

在示波法中，幅度系数法的个体适应性比较差，而波形特征法容易受外界干扰而缺乏稳定的测量精度.为了克服以上两种测量方法的缺陷，将两者结合起来，通过幅度系数法选取振荡波最大波幅A(MP)周围的若干个峰值，再根据波形特征法对这些峰值进行差分运算，寻找突变点.这样不仅能提高突变点判断的准确性，增强抗外界干扰能力，还可以降低运算量.

在脉搏振荡波中寻找峰值点，令脉搏振荡波与静压力信号的离散数据序列分别表示为D(n)=(d0,d1,…,dn-2,dn-1),C(n)=(c0,c1,…,cn-2,cn-1).通过对D(n)中每个数据与前一位数据进行比较，计算得到标志序列M(n-1)=(m0,m1,…,mn-3,mn-2).mk(0≤k≤n-2)的取值为

(5)

显然，标志序列M(n-1)通过取值+1和-1分别描述脉搏振荡波的上升和下降过程.

对标志序列M(n-1)中的每个数据与前一位数据进行相减，可得差值序列P(n-2)=(p0,p1,…,pn-4,pn-3).其中，pk(0≤k≤n-3)的取值为

(6)

此时，若pk=-2，则对应于离散数据D(n)中第k+1个数据为一个峰值点.因此，差值序列p(n-2)中取值为-2的元素有f个，表示脉搏振荡波有f个峰值点.

令峰值点对应的样点序号和幅值分别表示为Q(f)=(q0,q1,…,qf-2,qf-1),E(f)=(e0,e1,…,ef-2,ef-1).其中：qk表示第k个峰值点的采样序号，即在D(n)中的位置;ek为第k个峰值点的幅值.

比较E(f)中各峰值幅度的大小，找出最大值，即图1中对应脉搏振荡波的最大幅值A(MP).根据幅度系数法中的式(1)与式(2)，分别在E(f)中取定用于寻找突变点的范围{ea,eb}与{ec,ed}，即

(7)

式(7)中： a

设在[ea,eb]区间内的峰值点序列为Y(i)=(y0,y1,…,pi-2,yi-1).其中：y0=ea；yi-1=eb；i=b-a.通过对序列Y(i)中的每个数据与前一位数据进行相减，可得差值序列为Z(i-1)=(z0,z1,…,zi-3,zi-2).其中：zk=yk+1-yk(0≤k

3 Android端算法的实现

Android操作系统是Google于2007年发布的一个基于Linux平台的开源操作系统[8].近几年，Android手机逐渐应用于医学领域中[9-10].文中血压测量算法在Android移动平台上实现，并采用MVC(Model-View-Controller)模式，实现数据层与表示层的分离[11].

3.1View层的设计

View层主要负责接收从Controller层传来的数据并更新用户界面.用户界面包含一个“Start”按钮和两个文本编辑器，“Start”按钮用于启动子线程执行算法，文本编辑器用于显示舒张压和收缩压.

3.2Model层的设计

Model层包括滤波函数、突变点选择函数以及数据读取函数，完成数据的读取以及处理.Model层主要包括FilterAlgorithm.java，ReadData.java和Oscillography.java三个实现类.

1)ReadData.java类.实现从SDcard上读取数据.根据文本路径“filePath”，声明一个输入流Filefile=newFile(filePath),FileInputStreamfis=newFileInputStream()，通过一个while循环读取数据.

2)FilterAlgorithm.java类：负责滤波处理，包括如下两个函数(其中，filterContent为待滤波的离散数据，filterWidth为滤波半径).a)meanFilter(double[]filterContent,intfilterWidth)：通过一个for循环根据滤波半径不断对所得数据取均值以代替当前值.b)medianFilter(double[]filterContent,intfilterWidth)：通过嵌套的for循环计算滤波半径范围内的中值，以替代当前值.

3)Oscillography.java类.完成突变点选择算法，主要包括函数oscillography(double[]pulseData).该函数返回值为收缩压所对应的样点序号值systolicX.舒张压突变点选取的实现代码与此相类似.通过这两个突变点的序号，即可在静压力数据中找到对应的值，该值分别为收缩压和舒张压.

3.3Controller层的设计

Controller层是算法实现的核心控制层，主要体现在主线程对程序的整体控制.该层通过初始化UI控件、配置参数与信息、启动相关服务，以及实时监测外部事件控制整个流程的实现.

图6 Android端子线路实现流程Fig.6 Thread implementation flow chart of Android

设计中，主线程通过向UI界面传递数据，控制界面的刷新与显示；通过监听按钮的触发事件，开启新线程执行算法.考虑到一次性要处理的数据比较多，如果算法放在主线程中执行有可能导致主线程阻塞并出现异常，所以开启子线程执行算法.但是,Android系统中更新UI界面只能在主线程中完成，在子线程中更新UI界面是很危险的.因此，在主线程中声明Handler函数接收子线程的数据，并将该数据排入到主线程的队列中，更新UI界面[12].在主线程中，根据语句new Thread(new Mythread()) start开启子线程.子线程通过调用Model层中的函数，对数据进行分析处理并返回最后结果.子线程的设计流程图,如图6所示.

4 实验结果与分析

用于仿真的原始数据均来自于BP Pump2型无创血压监护测试仪(美国FLUKE公司).该仪器通过用户自定义模拟功能提供动态血压模拟，可提供的收缩压模拟范围为2.67～33.33 kPa，舒张压模拟范围为1.33～26.67 kPa.

4.1 滤波半径影响的仿真分析

在脉搏振荡波提取过程中，设第一次均值滤波半径为R1，中值滤波半径为R2，第二次均值滤波半径为R3.3组数据选取不同滤波半径时的Matlab仿真结果，如图7～12所示.图7，8中:ps为收缩压；pd为舒张压；R2=R3=10.图9，10中：R1=30；R3=10.图11，12中：R1=30；R2=10.

由图7，8可知：当R1在区间[20,50]时，收缩压取值平稳并较为准确；当R1≥30时，舒张压的取值准确并且趋于平稳.由图10，11可知：当R2在区间[4,10]时，收缩压取值平稳并较为准确；当R2在区间[2,10]时，舒张压的取值准确且趋于平稳.由图11，12可知：当R3≥8时，收缩压取值平稳并较为准确；当R3≥6时，舒张压的取值准确并且趋于平稳.

图7 R1对收缩压的影响 图8 R1对舒张压的影响 图9 R2对收缩压的影响Fig.7 Influence of R1 on Fig.8 Influence of R1 on Fig.9 Influence of R2 on systolic blood pressure diastolic blood pressure systolic blood pressure

图10 R2对舒张压的影响 图11 R3对收缩压的影响 图12 R3对舒张压的影响 Fig.10 Influence of R2 on Fig.11 Influence of R3 on Fig.12 Influence of R3 on diastolic blood pressure diastolic blood pressure systolic blood pressure

综上所述，文中在算法实现中采用的滤波半径为R1=30， R2=10， R3=8.

4.2 软件滤波仿真结果的比较分析

基于以上滤波半径的选取，分别对12组来自BPPump2的模拟血压数据进行测量，并分别与基于幅度系数法和突变点选择法的测量结果进行对比,结果如图13所示.图13中:pms为测量收缩压；pss为模拟收缩压；pmd为测量舒张压；psd为模拟舒张压；幅度系数法的系数取x1=0.5，x2=0.65.

(a) 收缩压 (b) 舒张压图13 收缩压和舒张压仿真对比图 Fig.13 Simulation comparison chart of systolic blood pressure and diastolic blood pressure

由图13(a)可知：经过Matlab仿真测量，基于突变点选择法测量的收缩压与pss的平均欧氏距离为1.40 kPa；基于幅度系数法测量的收缩压与pss的平均欧氏距离为0.65 kPa；基于三重软件滤波法测量的收缩压与pss的平均欧氏距离则为0.60 kPa.由图13(b)可知：经Matlab仿真测量，基于突变点选择法测量的舒张压与psd的平均欧氏距离为1.20 kPa；基于幅度系数法测量的舒张压与psd的平均欧氏距离为0.65 kPa；基于三重软件滤波法测量的舒张压与psd的平均欧氏距离则为0.45 kPa.

对比图13(a)，(b)的仿真结果可知：相比于突变点选择法与幅度系数法，三重软件滤波法仿真结果与原始模拟血压的平均欧氏距离均有所降低，和理论分析的结果是相符合的.

5 结束语

在示波法血压测量的基础上，提出软件滤波法与示波法相结合的算法，并在Android平台上实现.理论和实验结果均表明：1) 用软件滤波代替传统的硬件滤波确实可行，且可简化电路设计；2) 将幅度系数法和波形判别法相结合，在保证所需精度的同时，可降低突变点误判的概率和计算量；3) 算法执行简单有效，利于在Android移动平台的算法移植实现，具有良好的实用价值.但是，文中测量采用的数据均是模拟测量的数据，该方法应用于人体的数据测量结果是下一步要研究的内容.

[1] TAMURA T,MIZYJYRA I,SEKINE M,etal.Monitoring and evaluation of blood pressure changes with a home healthcare system[J].IEEE Transactions on Information Technology in Biomedicine,2011,15(4):602-607.

[2] 郑理华,窦建洪,何兴华,等.无创血压测量技术的改进与进展[J].中国医学装备,2013,10(3):49-52.

[3] 李雪情,张永亮,郑莹莹,等.基于示波法和高斯拟合的血压测量方法[J].传感技术学报,2010,23(12):1679-1685.

[4] 侯功,邓辉.基于示波法的血压测量新方法[J].现代电子技术,2012,35(22):147-150.

[5] 王维维,蒲宝明,李生金,等.基于示波法测量血压的算法改进[J].计算机系统应用,2012,21(2):196-199.

[6] CHEN Silu,BOLIC M,GROZA V Z,etal.Extraction of breathing signal and suppression of its effects in oscillometric blood pressure measurement[J].IEEE Transactions on Instrumentation and Measurement,2011,60(5):1741-1750.

[7] 于春梅,杨胜波.工程中几种实用软件滤波器的原理及应用[J].南通工学院学报,2001,17(3):18-20.

[8] 白文江.基于Android平台的移动应用开发研究[J].太原大学学报,2011,12(3):117-120.

[9] 张丹芯.基于Android 的智能医疗管理软件设计及其客户端的实现 [D].长春:吉林大学,2012:2-3.

[10] SUNG WenTsai,CHEN JuiHo,CHANG KungWei.Mobile physiological measurement platform with cloud and analysis functions implemented via IPSO[J].IEEE Sensors Journal,2014,14(1):111-123.

[11] 郑行双.基于MVC的Android与Web双模式教学平台的设计与实现[D].大连:大连理工大学,2013:5-7.

[12] 张亚杰.基于Android平台的移动终端应用程序的研究与开发[D].郑州:郑州大学,2013:36-38.

(责任编辑： 黄晓楠 英文审校： 吴逢铁)

Software Filter Based Algorithm for Oscillometric Blood Pressure Measurement and Its Android Implementation

XU Yongfeng1,2， HE Yucheng1,2, ZHOU Lin1,2

(1. College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China;2. Xiamen Key Laboratory of Mobile Multimedia Communications, Xiamen 361021, China)

To overcome the difficulties of conventional oscillometric blood pressure measurement in the extraction of pulse shock wave and the selection of waveform mutation point, an improved algorithm is presented that incorporates software filter into oscillometric method. In the software filter based algorithm, the pulse oscillation wave with distinguishable feature points is effectively extracted by a concatenated processing of software filter from the hybrid pressure signal samples, the mutation points are selected using the feature point method in a certain amplitude range determined by the amplitude characteristic ratios method, and the systolic and diastolic pressures are finally measured. The algorithm is simulated in Matlab, and implemented in intelligent mobile platform of Android. Simulation results in Matlab show that the algorithm can provide more reliable and accurate measurements of blood pressure.

blood pressure measurement; Android; oscillometric method; software filter

10.11830/ISSN.1000-5013.201704023

2016-12-30

贺玉成(1964-)，男，教授，主要从事无线通信和计算机网络的研究.E-mail:he_yucheng@163.com.

福建省自然科学基金计划资助项目(2014J01243)； 华侨大学科研基金资助项目(13Y0384)

TP 274.2

A

1000-5013(2017)04-0567-06