小学数学教学中画图助解方法初探

王悦

摘 要：小学生以形象思維为主，空间观念有待发展，对于一些较复杂的题目，在教学过程中教师应重视引导学生以图助解，化难为易。采用画示意图变抽象为具体、画直观图变片面为周全、画线段图变隐蔽为直观等方法，以图助解直观揭示数量关系，既可增强数学教学的趣味性，同时又将提高学生的解题能力，促进学生智力发展。

关键词：画图 解题能力 小学数学

中图分类号：G623.5 文献标识码：C 文章编号：1672-1578（2017）06-0196-01

在小学数学教学过程中，教师应重视引导学生用简单的图形把题目的意思表示出来，或者把自己的思维过程用画图的方法表达出来，这样能帮助学生将复杂的问题简单化，形成有效的解决问题的思路，也能很好地培养学生的数学直观能力和数形结合的思想。

1 画示意图，变抽象为具体

小学低年级的学生由于词汇量较少，他们的思维又是以具体的形象思维为主，对于一些解决问题的题目，不能很好地从中抽象出数学模型。这时候，画图就起到了一种“桥梁”的作用，它能很好地使学生用数学的眼光去解释生活中的一些现象，解决生活中的一些问题。

例如：一年级数学中的排队问题：（1）小朋友排队，小明前面有9人，后面有5人。这一队一共有多少人？（2）小朋友排队，从前往后数小明排第9个，从后往前数小明排第5个。这一队一共有多少人？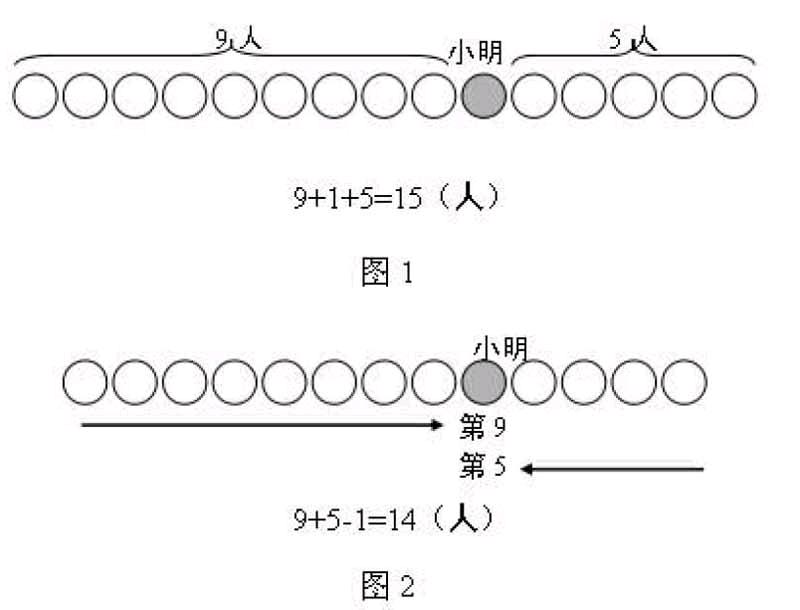

学生在解答这两类题时，很容易错误地列出了算式“9+5=14（人）”。教师可引导学生用自己喜欢的符号表示小明和别的小朋友，动手画一画。

这样两幅图将抽象的问题变的具体直观，问题迎刃而解。此时切莫停止探究的脚步，教师可继续利用这两幅图引导学生进行比较，让学生在比较中深入理解两道题的异同。明白什么时候“小明”没有被数的，什么时候“小明”是重复数的，在解决此类问题时做到不遗漏、不重复，同时也让学生在自己看得懂的数学画中体会基数和序数的奇妙。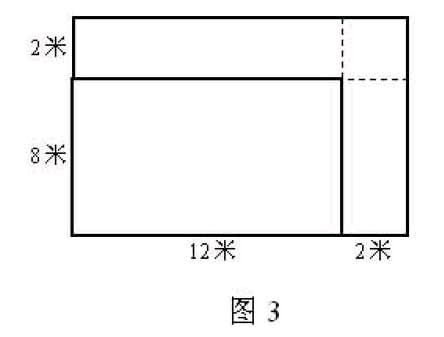

2 画直观图，变片面为周全

对于小学生来说，几何初步知识是他们学习过程中最薄弱的环节，学生常常缺乏解决问题的策略，出现因考虑问题片面而失误的情况。教师如果能引导学生画直观图，这样学生的思维会由片面变为周全，也会逐步形成依托图形灵活、有效地解决不同问题的能力，从而增强策略意识，发展空间观念。

例如：一个长方形，长12米，宽8米。若长和宽各增加2米，面积增加了多少平方米？

学生在解答这一问题时，往往片面地认为增加部分是一个面积为“2×2=4（平方米） ”的正方形。如果画出直观图，问题的本质一目了然。

画出直观图（图3），数量关系比较隐蔽的长方形面积计算问题会变得直观清晰。教师在此基础上可进一步引导学生一题多解，在发展空间观念的基础上，培养学生的发散思维能力。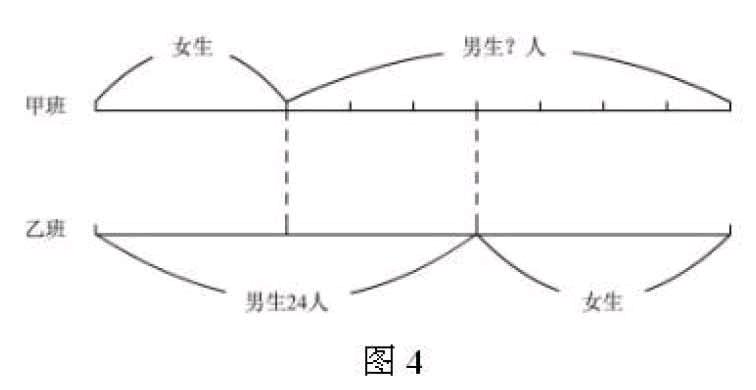

解法一：新的长方形面积-原来长方形面积=增加部分的面积。（12+2）×（8+2）-12×8=44（平方米）

解法二：直接算增加部分面积。12×2+2×2+8×2=44（平方米）

解法三：增加部分可以拼为一个长（12+2+8）米，宽2米的长方形。（12+2+8）×2=44（平方米）

学生体验了画图的优势，解题思路多样化，在获得解决实际问题的成功体验后，也提高学好数学的信心。

3 画线段图，变隐蔽为直观

画线段图是把数学与图形相结合，用图形来揭示数学问题中的数量关系。分数、百分数应用题对于小学生来说比较抽象，不容易理解，教师如果能重视引导学生借助线段图弄清有关数量与标准量的对应关系，就能变隐蔽为直观，找到解题的途径。

例如：甲班和乙班人数相等。甲班女生人数相当于乙班男生人数的1/2；乙班女生人数相当于甲班男生人数的4/7。已知乙班有男生24人，甲班有男生多少人？

由于条件的叙述婉转含蓄，造成学生解题的困难。这时教师可引导学生作图，把互相比较的两个量画在同一边，如图4：

从图上容易看出，甲班男生人数的（1-4/7）和乙班男生的

1/2相等。找到了解题的方法：24×1/2÷（1-4/7）=28（人）。

画线段图可以将应用题的条件由抽象变为具体，由隐蔽变为直观，教师如果能重视引导学生灵活巧妙画图，学生就会在画图的过程能找到解题的捷径，体验成功的乐趣，有利于提高学生的思维能力和学习数学的兴趣。

以图助解，直观地揭示了数量关系，拓宽了解题思路，使枯燥难懂的数学变得简单趣味。以图助解，提高了学生的解题能力，促进了学生智力的发展。如果教师能积极引导，学生的创造力、想象力会在画图的过程中迸发，数学的美会在数形结合中绽放。