最后一公里配送路径优化研究

章雪岩，桂 欣，郑巧然

（西南交通大学 交通运输与物流学院，四川 成都 610031）

最后一公里配送路径优化研究

章雪岩，桂 欣，郑巧然

（西南交通大学 交通运输与物流学院，四川 成都 610031）

根据最后一公里配送的业务特点，对最后一公里配送路径优化问题进行了研究，建立了适合启发式算法求解的配送优化模型，并结合遗传算法的思想设计了算法。从模拟仿真的角度证明该方法对求解最后一公里配送的优化问题具有简单可行、计算效率高、并行能力强、自动学习的特点。

最后一公里；配送路径；路径优化；遗传算法；线上到线下

1 引言

近年来，由于电子商务O2O等模式的兴起，使得最后一公里配送的研究变得热门。O2O最难解决的就是“最后一公里问题”，也就是物流配送或者针对用户在线下送货上门服务。最后一公里配送从定义上来说，是指供应链中到最终顾客手中的最后一段短距离配送，并不是真正意义上的“最后一公里”，属于电商平台的线下部分[1]。由于在这一段配送过程中，处于供应链过程的末端，属于零担运输，需求点多，货物种类多，同时直接与客户交互，提供给顾客服务，是供应链中最为复杂且最为重要的一环[2]。

结合电商平台快递配送、外卖配送等实际业务的考虑，客户关注配送的等待时间，而配送员关注配送的成本[3]。在实际操作中，无论外卖还是电商快递都是两阶段优化的。第一阶段，根据客户平均等待时间和订单下达时间划分不同快递员配送的订单；第二阶段，不同的快递员根据订单的分布规划自己的配送路线。在这两阶段中，其中第一阶段一般由配送平台根据数据挖掘结果结合平均服务时间进行安排。而第二阶段目前还是依靠人工经验。这两阶段都是服务质量和成本之间的均衡，但在第二阶段往往因为人为因素导致不合理情况的出现，例如快递员不合理配送导致顾客等待太长时间、运程增加等。因此，本文结合遗传算法从车辆路径问题（VRP，Vehicle Routing Problem）的角度对最后一公里配送的第二阶段进行优化研究。

VRP是一个NP-hard问题，求解算法有精确算法和人工智能算法，在规模小且可求解情况下，精确算法优于人工智能算法[4]，但要在有限时间内找到大规模问题的满意解、可行解，启发式算法具有无与伦比的优势[5]。我国目前使用最广泛的电子商务物流配送模式是送货上门模式，随着碳排放研究、生鲜配送等O2O模式的开展，单纯的对服务质量的研究开始转为对配送效率和配送成本节约的研究。虽然最后一公里配送还有自助收发箱模式、顾客自提模式等，但其本质还是快递员追求配送效率和顾客追求服务质量之间的矛盾。最后一公里在抽象为VRP问题时，通常有带时间窗的车辆路径问题（VRPTW）、容量限制的车辆路径问题（CVRP）、需求可拆分的车辆路径问题（SDVRP）等，但在实际中，最后一公里问题中诸如时间、服务对象等约束不是那么苛刻，更多是希望在提升效率的同时获取顾客认同和快速求解的能力。因此本文从快递员和客户这两个角度出发，结合容量限制提出了快速求解的CVRPGA算法。

2 最后一公里配送VRP模型

2.1 问题描述

一般来说，快递员运载工具的货物容量是有限的，且在最后一公里配送过程中，货物种类繁多，其快递包装不统一，同时客户签收对快递包装有一定的要求，导致有限的运载容量难以充分利用；矛盾在于快递员想尽量的缩短配送路径，同时避免在某一地点停留太久，以缩短工作时间和提高服务效率。因此如何规划自己的配送路线是快递员最该考虑的问题。从线性规划的角度来说，该问题的求解目标是快递员行走的路径最短，存在的约束条件有：

（1）快递员驾驶以配送点作为起点和终点；

（2）每个配送点的需求必须得到满足，一般来说配送点的需求不超过运载工具的容量Q；

（3）在每次快递员接单过程中，其行程不超过L，以降低单次快递配送中快递平台通知客户收取包裹信息的牛鞭效应，使得客户等待时间较少，维持一定的服务质量。

从上述分析可以看出，该规划问题是一个典型的车辆能力约束的车辆路径问题（Capacitated Vehicle Routing Problem，CVRP）。最后一公里配送的CVRP问题可以描述如下：存在图G=(V,E)，其中节点集合V={0,1,2,...,n}代表1个配送中心和n个需求点，边的集合E={(i,j)|0≤i≠j≤n}代表任意两节点形成的边，边长用dij表示。设快递员驾驶容量为Q的车从配送中心出发回到配送中心，n个节点的需求量分别是q1,q2,...,qn，边长dij和需求qi已知，且max(qi)≤Q。现在目标是快递员可以多次往返配送中心，往返次数为m，满足配送点的需求，但希望总路径长度最短。

2.2 模型建立

通过上述分析可以得出，最后一公里配送的CVRP问题的数学规划模型如下：

目标函数：

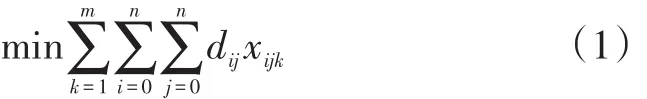
约束条件：

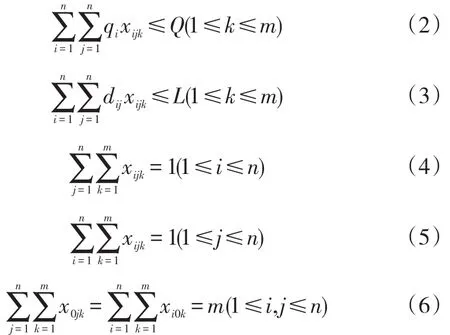
其中xijk为0,1变量，表示快递员第k次服务的快递点集合Vk，具体的：

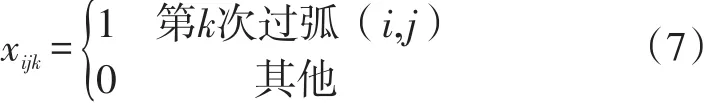
式（1）为目标函数，表示快递员一共m次所配送的总路径长度；式（2）为每辆车单次配送的容量约束；式（3）为快递员单次配送的距离约束（为保证服务质量）；式（4）、（5）表示快递员只经过服务点一次；式（6）约束了所有车辆起始终点都在配送中心。

上述模型精确描述了最后一公里的CVRP问题,但不利于对遗传算法执行细节的理解,从集合的角度将上述问题等价转换如下[6]：

目标函数：

约束条件：

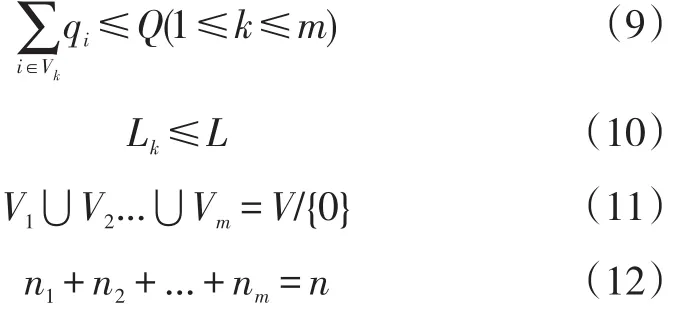
其中Vi、ni分别是第i次的路径集合和路径集合中经过配送点的数量。从式（8）-（12）可以看出，启发式算法下CVRP模型的关键在于如何在既定条件下划分快递员的配送次数和配送顺序，使得总路径最短。

3 最后一公里配送的遗传算法

3.1 遗传算法原理

遗传算法是基于生物进化提出的一种启发式算法，通过模拟自然进化过程来进行最优解的搜索。遗传算法认为最优解是最满足适应度的种群中的最优个体，为了得到这个个体，一个种群的基因通过不断的复制、组合交叉、变异适应新的环境，产生新的解。一般为了效率考虑，设定一个迭代上界，把末代种群中的最优个体经过解码，作为求解问题的满意解。其实现步骤如图1所示。

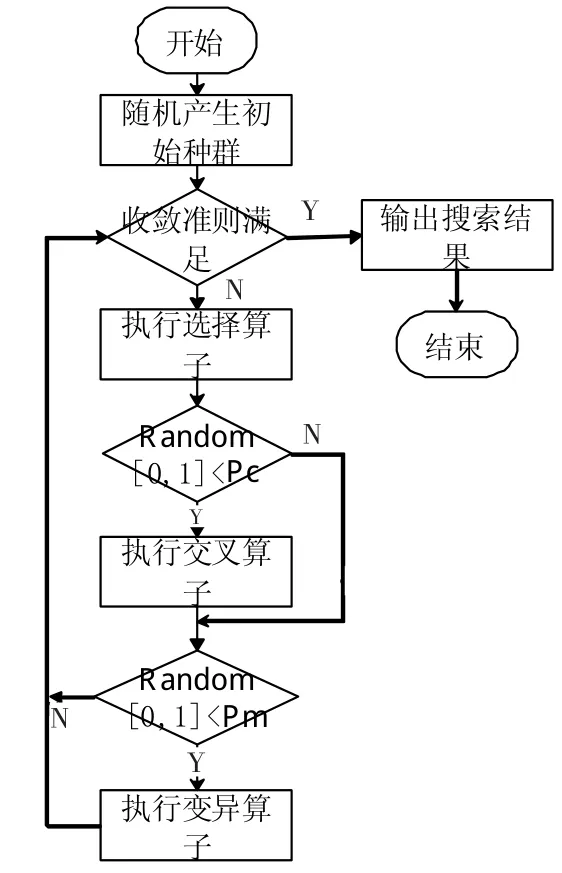
图1CVRPGA算法流程图

遗传算法从种群的角度考虑解的搜索，这种策略相比传统优化算法而言，它从多个初始值开始迭代，覆盖面广，不易陷入局部最优解；同时对解的评价是通过适应度函数，面对搜索空间中的多个解进行评估，利于计算的并行化；从算法的思路来说，其本身是自组织、自适应和自学习性的，对复杂问题的求解具有很强的应变能力。为了促进遗传算法的收敛，避免种群的早熟，就一般而言，遗传算法的参数选取存在一定的经验值[7]：

（1）种群规模。当种群规模太小时，会出现明显的近亲交配，产生病态基因，虽然可以采用较大概率的变异算子，但一般效果不明显，且对已有模式的破坏作用极大。同时如果种群规模太大，结果难以收敛会浪费资源，稳健性下降，结合现有的研究，一般种群规模建议在100以内。

（2）变异概率。变异是遗传算法中增加种群多样性的一种方式。如果变异概率太小，种群多样性下降会特别快，导致有效基因迅速丢失；如果变异概率太大，容易破坏高阶模式。变异概率一般取0.000 1-0.2。

（3）交配概率。交配是生成新种群最重要的手段，与变异概率类似，交配概率太大容易破坏已有的有利模式，随机性增大，易错失最优个体；交配概率太小不能有效更新种群。交配概率一般取0.4-0.99。

（4）进化代数。遗传算法是一个逐步优化的算法，需要一定的进化时间。进化代数太小，算法不容易收敛，种群没有成熟；代数太大，会额外的浪费时间，一般进化代数取100-500。

（5）种群初始化。初始种群的生成是随机的，但可以考虑在开始时对实际问题进行简单分析，进行一个大概的区间估计，将解尽量靠近最优解的解集空间。

3.2 最后一公里配送优化算法设计

遗传算法的关键在于初始种群的生成、基因编码、适应度函数的设计、选择算子、交叉算子的选择和处理等。本文结合最后一公里配送的业务特点进行如下的选择。

（1）基因编码。基因编码是在遗传算法求解过程中，选择合适的方法表示该问题的可行解。常用的编码有二进制编码、实数编码、矩阵编码和量子编码等[8]。其编码方式、优缺点和适用范围存在不同的特点。最后一公里配送过程中，其配送点规模较大，实数编码直接采用解空间的形式，无需特别解码，且编码意义直观清楚。例如对于存在9个配送点的最后一公里配送的一个基因，其染色体（0,4,5,3,0,2,8,6,0,7,1,9,0）表示快递员分三次完成9个配送点的配送任务，配送路线如图2所示。

图2 实数编码的染色体（0表示配送中心）

（2）初始种群的生成。初始种群的生成一般采用随机策略，本文利用matlab生成随机的实数序列，根据容量约束确定配送员需要配送的次数，从最低次数开始调整，插入实数序列的0值，进行初始种群的生成。一般而言，可以运行多次，将上一次的结果作为输入，提高效率。

（3）适应度函数设计。遗传算法依据适应度函数的值来区分种群个体的优劣，适应度值大的个体有更多的机会繁衍后代。适应度函数在设计时要满足单值、连续、非负、最大化的函数特性；在适应度函数曲线上，各点的优劣性成反比例，保证合理性、一致性；同时其计算量不能太大；且在一致问题上具有广泛的通用性[8]。在上述准则下，设计最后一公里配送优化问题的适应度函数如下：

式（13）中的M为惩罚因子，一般取一个较大的实数。

（4）选择算子。选择算子是遗传算法中根据个体的适应度对种群中的个体进行优胜劣汰操作的过程，使得适应度大的个体有较大的概率遗传到下一代群体中。轮盘赌选择方法是经典且成熟的选择算子，采用回放式随机抽样的方式进行选择，保证个体选中的概率与适应度成正比，采用轮盘赌选择算子的最后一公里配送的基因选择大致如下：

①计算配送路径每个染色体xi的适应度值 f(xi)，i=1,2,...,N。

②计算每个配送路径染色体编码遗传到下一代种群中的概率P(xi)。

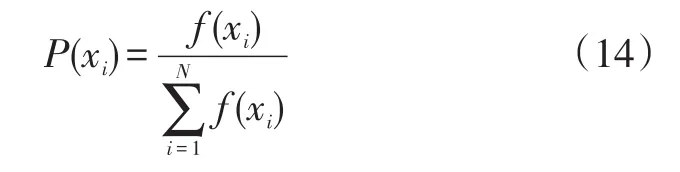
③计算每个配送路径染色体编码的个体累计概率Ti。

④随机产生一个（0,1]之间的随机数r，根据q[k-1]＜r≤q[k]选择路径染色体编码k。

（5）交叉算子。交叉是指把两个父代个体部分结构进行重组形成新的个体，在最后一公里配送问题上，是指在两个配送方案中，进行部分配送节点的调整，完成对方案的改进（如图3所示）。

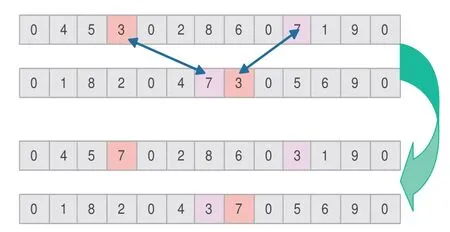
图3 交叉算子示意图

（6）变异算子。同交叉算子一样，变异算子也是一种随机进化后代的策略，在配送路径上表现为单个配送方案的内部调整（如图4所示）。

图4 变异算子示意图

（7）自适应过程。交叉概率Pc和变异概率Pm的选择对遗传算法的行为和性能都有一定的影响。结合对自适应遗传算法AGA和改进的自适应遗传算法IAGA的研究[10]，为了加快算法效率，提出以下据适应度对变异概率做出调整的方法。

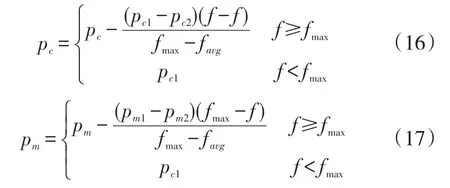
式（16）、（17）的改进使得交叉概率和变异概率根据个体的适应度在平均适应度与最大适应度之间线性变换，采用精英保留策略，保证了每一代的优良个体不被破坏。

（8）迭代停止条件。在最后一公里配送问题的求解上，往往不在意取得算术上的最优解，而是快速的获取相对经济的配送方案。从这个思想出发，最后一公里配送优化的迭代停止条件考虑如下：

①从种群进化稳定性出发，设置一个ε，当种群进化出现max(f(xi))-averg(f(xi))≤ε就停止迭代。

②设置一个最大迭代次数，一般根据问题求解的经验取得，在不满足种群稳定性的条件下，为了算法效率，迭代到最大迭代次数时取其为满意解。

4 实例应用

在某个电子商务平台的运营过程中，一快递员一共接到12个收货点的订单，快递员单次可携带的最大重量为20个单位，其中配送中心在快递员取包裹时短信通知客户，为了保证较少的客户等待时间和对快递员效率的监控，一般每次给快递员的包裹配送总行程不超过35个单位，以配送中心为（0,0）建立坐标，各配送点的坐标和配送量见表1。

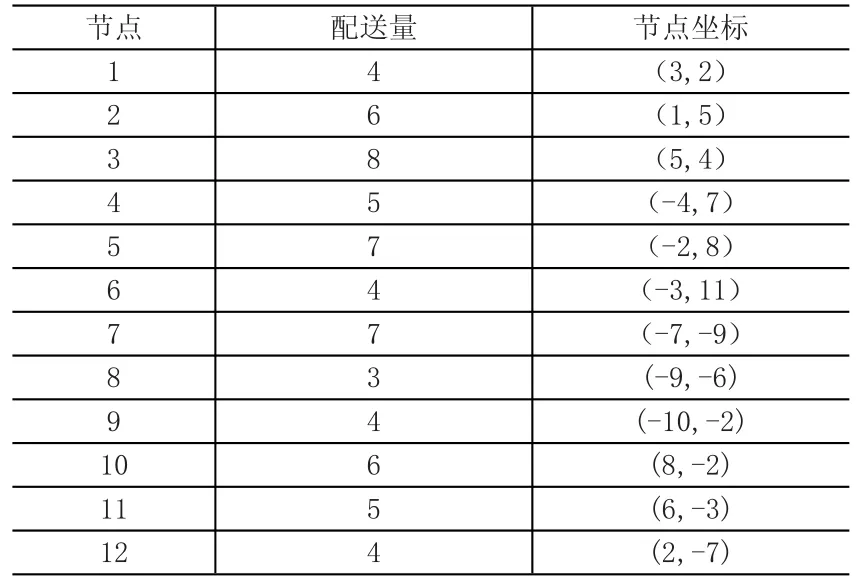
表1 各节点数据

利用式（1）-（7）的线性规划模型，结合lingo软件精确求解得最优的配送总路程为78.52，一共配送4次，迭代4 249次，平均耗时2.12s，子路径见表2。

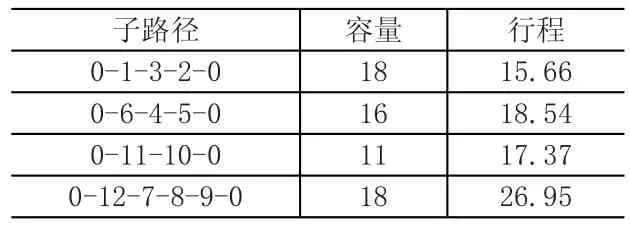
表2 lingo精确求解结果

结合式（8）-（12）的CVRPGA问题，利用matlab实现算法，其相关参数设置为：种群规模N=100，惩罚因子M=100 000，最大遗传代数G=200,初始交叉概率Pc=0.9，初始变异概率Pm=0.1，ε为10-5。随机求解100次，平均耗时3.34s，求解结果的惩罚因子值如图5所示；随机抽取100次结果的10个解，见表3；改变点的规模，求解平均耗时如图6所示。

图5 随机求解100次结果

表3CVRPGA算法的满意解

从图5和表2可以看出，在随机100次求解情况下，有效解为92个，满意解个体也足够优秀，能够找到问题的解；结合图6的耗时比较，可以看出CVRPGA算法耗时经济。因此在求解最后一公里配送路径优化问题时，CVRPGA能够有效得到满意解，满足O2O条件下的急速配送需求。

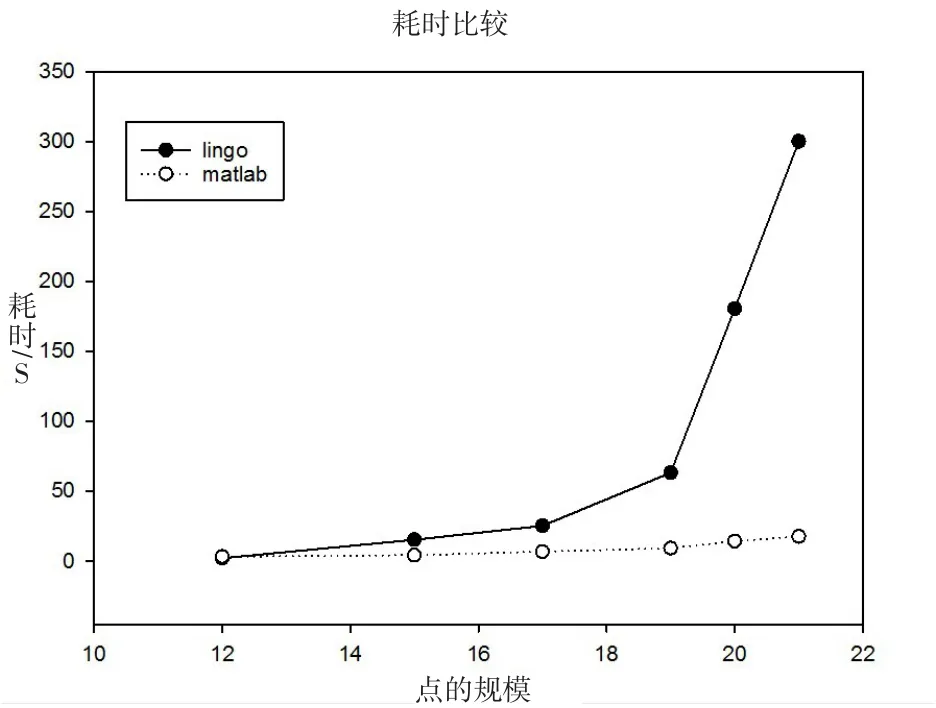
图6 不同规模下的求解耗时

5 结语

从上述分析可以看出，在求解最后一公里配送优化问题上，CVRPGA算法具有适应度强，并行化程度高，收敛速度快的特点。在快速求解满意解的角度上，该算法为解决最后一公里配送问题提供了新的思路，是解决O2O难题的一种新方法。

[1]詹斌,谷孜琪,李阳.“互联网+”背景下电商物流“最后一公里”配送模式优化研究[J].物流技术,2016,(1)：1-4.

[2]杨岩.我国电商物流最后一公里配送问题研究[J].物流工程与管理,2014,(10)：90-91.

[3]黄验然,吴光先.电子商务最后一公里配送的收货模式研究[J].嘉应学院学报,2014,(4)：37-41.

[4]贾楠,吕永波,付蓬勃,等.物流配送问题中VRP的数学模型及其求解算法[J].物流技术,2007,(4)：54-56.

[5]史玉敏.物流配送环节中车辆路径问题（VRP）的研究[D].济南：山东师范大学,2007.

[6]饶卫振,金淳.求解大规模CVRP问题的快速贪婪算法[J].管理工程学报,2014,(2)：45-54.

[7]卓金武.MATLAB在数据建模中的应用[M].北京：北京航空航天出版社,2011.

[8]张超群,郑建国,钱洁.遗传算法编码方案比较[J].计算机应用研究,2011,(3)：819-822.

[9]刘英.遗传算法中适应度函数的研究[J].兰州工业高等专科学校学报,2006,(3)：1-4.

[10]李欣.自适应遗传算法的改进与研究[D].南京：南京信息工程大学,2008.

Study on Route Optimization in Last-mile Distribution

Zhang Xueyan,Gui Xin,Zheng Qiaoran
(School of Transportation&Logistics,Southwest Jiaotong University,Chengdu 610031,China)

In this paper,according to the operational characteristics of the last-mile distribution,we studied the route optimization in the last-mile distribution process,built the distribution optimization model that can be solved using the heuristic algorithm and then based on the genetic algorithm,designed an effective solution to the model.From the angle of simulation,we proved the convenience,feasibility,high efficiency and other superiorities of the method in solving the optimization issues in the last-mile distribution.

last mile;distribution route;route optimization;genetic algorithm;online to offline

F224.0；F252.14

A

1005-152X(2017)06-0116-06

10.3969/j.issn.1005-152X.2017.06.027

2017-05-06

章雪岩（1957-），男，西南交通大学教授，研究生导师，管理学博士，研究方向：物流信息化、供应链管理；桂欣，男，西南交通大学物流工程专业研究生；郑巧然，女，西南交通大学物流工程专业研究生。