带装甲钢背板的钢纤维混凝土靶抗侵彻试验及数值模拟研究
冯君, 孙巍巍, 刘志林, 王晓鸣
(1.南京理工大学 瞬态物理国家重点实验室, 江苏 南京 210094; 2.南京理工大学 机械工程学院, 江苏 南京 210094;3.南京理工大学 理学院, 江苏 南京 210094)
带装甲钢背板的钢纤维混凝土靶抗侵彻试验及数值模拟研究
冯君1,2, 孙巍巍3, 刘志林2, 王晓鸣2
(1.南京理工大学 瞬态物理国家重点实验室, 江苏 南京 210094; 2.南京理工大学 机械工程学院, 江苏 南京 210094;3.南京理工大学 理学院, 江苏 南京 210094)
为了研究钢纤维混凝土抗侵彻性能,对带装甲钢背板的高强度钢纤维混凝土靶进行12.7 mm穿甲弹、长杆弹高速撞击侵彻试验。根据背靶侵彻深度试验结果,采用防护系数评估复合靶的抗侵彻性能。采用细观离散元模型Lattice Discrete Particle Model、弹塑性模型和Johnson-Cook屈服准则分别描述钢纤维混凝土、弹体和装甲钢靶的材料力学响应,建立了混凝土侵彻问题的有限元- 离散元耦合数值仿真模型。通过对比钢纤维混凝土破坏形态和背靶侵彻深度,验证仿真模型对于钢纤维混凝土侵彻问题的适用性。针对3种代表性侵彻工况,模拟分析复合靶间隙以及钢纤维含量对于侵彻响应的影响。仿真结果表明:相比含间隙的复合靶,无间隙的约束条件能够明显减小背靶侵彻深度;钢纤维含量对于背靶侵彻深度几乎没有影响而对混凝土靶破坏形态有较大影响。进一步仿真分析12.7 mm穿甲弹贯穿钢纤维混凝土靶板响应影响因素,得到:圆柱靶直径大于30倍弹径时,弹体贯穿出靶速度趋于收敛;随着靶体厚度增小,剩余速度与撞击速度趋近于线性关系。
兵器科学与技术; 钢纤维混凝土; 抗侵彻; 数值模拟; 贯穿响应
0 引言
混凝土特性是抗压不抗拉,加钢纤维“乱丝”后,其抗拉、抗剪性能有很大提高。纤维对于基体裂纹产生或扩展有抑制作用[1-3],导致应变硬化响应,因此钢纤维混凝土材料比素混凝具有更好的抗拉、抗剪、吸能效果,因此在防护工程、机场跑道等抗爆炸、侵彻结构中有很好的应用前景[4-5]。钢纤维混凝土侵彻问题成为当前冲击工程领域研究热点问题,弹体冲击钢纤维混凝土是一个涉及靶体材料大变形、高应变率和高压的过程,涉及断裂、破碎等复杂响应[6-7]。采用空腔膨胀分析等理论方法获得控制方程组的求解非常复杂且侵彻过程的工程模型存在太多简化和假设[8-9],因此基于理论的工程分析模型在研究复杂工况的侵彻问题存在局限性。近年来随着无网格方法、多尺度模拟等计算力学技术的发展,出现了越来越丰富的数值计算手段和模型(物质点法、微平面法等[10]),仿真技术成为研究混凝土侵彻问题的重要手段。
基于离散假设,Cusatis等[11-12]开发出了一种模拟水泥基体内部骨料相互作用的细观离散元模型(LDPM)。根据混凝土骨料级配信息在几何体内部随机生成骨料颗粒,并在其周围构建潜在裂纹微面以及细观本构关系。LDPM模型能够模拟混凝土材料断裂、多轴响应、尺寸效应等[12],并在钢纤维混凝土结构受到冲击与爆炸等动态载荷工况模拟中获得较好结果[13-14]。对比有限元模型中采用删除单元来模拟侵彻、裂纹扩展等现象,离散元模型避免了单元删除带来的质量、能量不守恒,在模拟分析混凝土破坏失效等不连续问题中具有巨大优势。
本文对带装甲钢背板的钢纤维混凝土靶进行侵彻试验,结合防护系数定量分析复合靶抗侵彻性能。结合LDPM仿真,对复合靶侵彻响应、钢纤维靶板贯穿响应的不同影响因素进一步模拟分析。
1 钢纤维混凝土复合靶侵彻试验
1.1 钢纤维高强度混凝土的制备
与普通混凝土不同,高强度混凝土主要由细骨料、粉煤灰和少量水组成,其配比关系如表1所示。各组分信息如下:水泥,52.5号普通硅酸盐水泥;高强度细骨料直径为1~3 mm;砂,采用矿物成分石英,最大粒径为600 μm,平均粒径为250 μm的细砂;硅灰,平均粒径0.1~0.3 μm,勃氏透气比面积仪器测得比表面积为20~28 m2/g;石英粉,平均粒径为40 μm,SiO2含量98%,比表面积4 067 cm2/g.

表1 混凝土成分组成Tab.1 Concrete mixture and proportion
为了钢纤维掺杂的经济性、可操作性,本文选择长6 mm、直径0.2 mm的直钢纤维,其拉伸强度和杨氏弹性模量分别为1.2 GPa和210 GPa.
高强度钢纤维混凝土的浇筑流程如下:1)将水泥、砂、石英和硅灰按照配比称量好,倒入搅拌锅中,搅拌3 min;2)加入溶有减水剂的一半用水,搅拌3 min;3)倒入所需的另一半水,搅拌5 min;4)将所需的钢纤维分散撒到新鲜流质混凝土中,搅拌2 min,任意方向充分散布纤维到水泥基体中;5)将混合物倒入浇筑模具中,并振动模具2 min,确定新鲜混凝土充满整个模具。用铲子清理模具边缘,盖上塑料薄膜防止水分蒸发;6)充分振动试件,并将其放在恒定的22 ℃温度和100%湿度的室内环境下,24 h之后脱模。28 d养护之后,高强度钢纤维混凝土密度测量结果为2.45 g/cm3。对于150 mm边长的试块进行单轴压缩试验,获得混凝土压缩强度约为300 MPa,而杨氏模量在55~60 GPa之间。
1.2 带装甲钢背板的钢纤维混凝土靶抗侵彻试验
为了研究复合靶抗侵彻性能,本文采用两种弹头进行侵彻试验:1)12.7 mm穿甲弹,其弹芯尖卵形头部曲率半径比值为3、直径为10.8 mm,质量为30 g,对均质装甲钢的侵彻威力约为30 mm;2)1∶4.7底推式杆式模拟弹,即长杆弹,其直径为6 mm,弹头长度13 mm,质量为44.5 g,对均质装甲钢的侵彻威力约为70 mm. 两种弹体的照片和详细尺寸如图1所示,其中长杆弹尾部设计成圆台状,以获得更好的飞行稳定性。

图1 侵彻试验弹体及其尺寸Fig.1 Projectiles and their dimensions
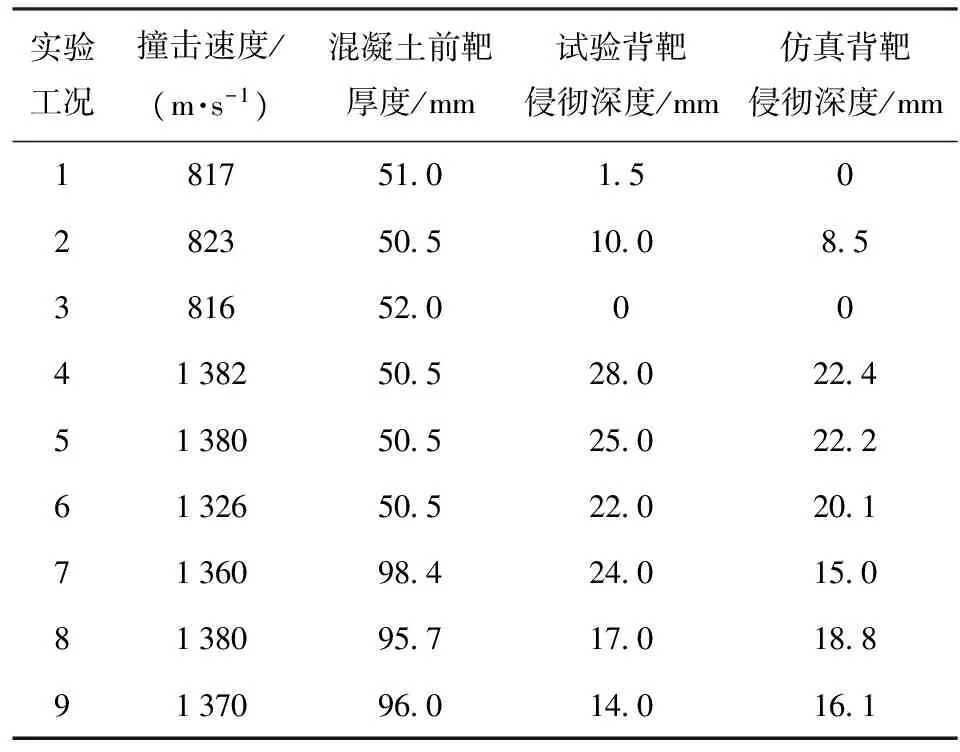
侵彻试验装置如图2所示,主要包括枪弹发射装置、弹托回收装置、测速装置和带装甲钢背板的钢纤维混凝土靶。钢纤维混凝土靶体直径尺寸为穿甲弹侵彻复合靶试验结果见表2,由于混凝土浇筑中存在缩水现象,不同试验号的靶体厚度稍有差别,820 m/s左右撞击速度侵彻,得到的背靶侵彻深度分别为1.74 mm、10 mm和0 mm. 其中,3号试验结果显示弹体贯穿了混凝土前靶,但没能在背靶产生开坑侵彻。结合1号和2号试验,穿甲弹以820 m/s左右撞击速度侵彻50 mm厚高强度钢纤维混凝土+30 mm厚装甲钢复合靶,在背靶留下大概侵彻深度在10 mm之内,该工况下复合靶的抗侵彻性能对应的防护系数在1.27~1.80之间。长杆弹侵彻试验结果见表3,由于发射速度更高,其侵彻威力比穿甲弹更强。类似工况下,7号与8号、9号侵彻试验剩余侵彻深度差别较大,这可能是由于养护条件不够导致7号试验中混凝土前靶强度较低。长杆弹体以1 380 m/s左右撞击速度侵彻带装甲钢背板的50 mm、100 mm厚高强度钢纤维混凝土靶,复合靶抗侵彻的防护系数分别约为2.67和1.77.
100 mm,厚度有50 mm和100 mm两种;背靶采用603装甲钢,厚度也分为30 mm和60 mm两种。
复合靶的抗侵彻性能通常采用防护系数来表示,本研究采用文献[7]中的差分效益系数:
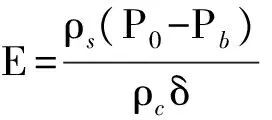
(1)
式中:ρs、ρc分别为装甲钢背靶和混凝土前靶的密度;P0是弹体单独侵彻背靶防护时的侵彻深度;Pb是弹体侵彻复合靶时背靶剩余侵彻深度;δ是混凝土前靶厚度。

图2 侵彻试验装置Fig.2 Penetration test setup

表2 穿甲弹侵彻复合靶结果Tab.2 Experimental results of armor-piercing projectile penetrating a composite target

表3 长杆弹侵彻复合靶结果Tab.3 Experimental results of long rod projectile penetrating a composite target
侵彻试验后,收集到破坏的高强度钢纤维混凝土靶板如图3所示,其中图3(a)为迎弹面视角靶体破坏,而图3(b)为靶背面破坏情况。由于弹体高速碰撞且靶体截面较小,虽有钢纤维作用,弹着点附近的混凝土材料受到冲击载荷仍然发生粉碎崩落,圆柱靶整体发生辐射状破坏成多块扇形体。图4给出了2号、5号侵彻试验中装甲钢背靶迎弹面破坏形态,图4(a)表明2号试验中弹体只在钢靶上留下较浅划痕,而图4(b)显示5号试验在背靶中形成开坑和垂直于靶面的侵彻隧道段。

图3 钢纤维混凝土靶破坏形态Fig.3 Steel fiber reinforced concrete target damage mode

图4 背靶破坏形态Fig.4 Back armor steel target damage mode
2 纤维混凝土LDPM离散元模型
本文选取LDPM离散元模型对钢纤维混凝土材料进行描述。首先,根据Fuller级配曲线将骨料颗粒等效成不同直径的圆球随机投放在混凝土体内部。由于水泥基体材料以及骨料与基体交界面相比于骨料,其强度和刚度都要弱很多,LDPM假设混凝土裂纹都发生在基体和基体/骨料接触面。通过Delaunay技术等生成在骨料颗粒周围形成三角形潜在裂纹微面组成的多面体包络面LDPM单元,如图5(a)所示。由骨料颗粒位置和尺寸生成的三角形潜在裂纹微面,其具体几何信息及其拓扑关系详见文献[11,15]。

图5 LDPM单元及其内部细观结构[15]Fig.5 LDPM element and aggregate particle[15]
采用刚体动力学描述细观模型系统的变形,将细观应变在N、L、M3个方向上的投影分量,用潜在裂纹微面中心位置的位移[uc]来表示:
(2)
式中:l是相邻骨料间距;N、L和M是定义潜在裂纹微面上局部坐标系的单位向量。在文献[16-17]中,Cusatis等证明了(2)式的细观应变定义与连续介质力学中应变在多面体微面上投影分量一致。
2.1LDPM本构关系
在弹性响应阶段,法向和切向细观应力与对应的细观应变呈线性关系:tN=ENeN,tM=ETeM,tL=ETeL,其中细观法向模量为EN=E0,细观切向模量为ET=αE0,E0是等效法向弹性模量,α是切向- 法向耦合系数。对于非线性响应阶段,LDPM主要考虑以下3个方面的细观力学响应:断裂、空隙坍塌和压实以及压剪耦合内摩擦[11]。
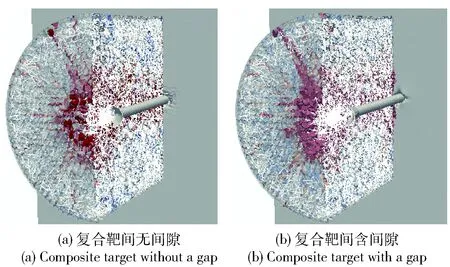
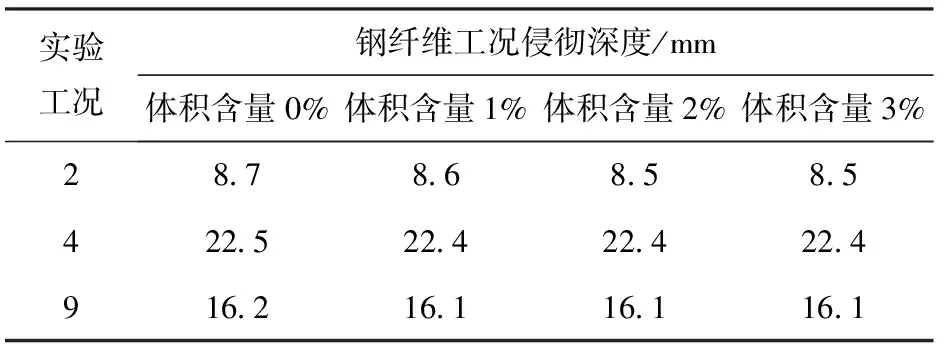
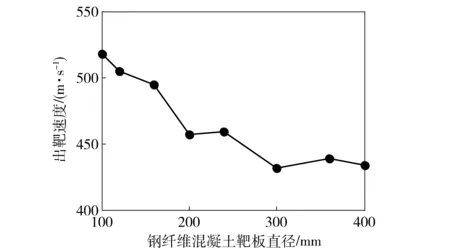
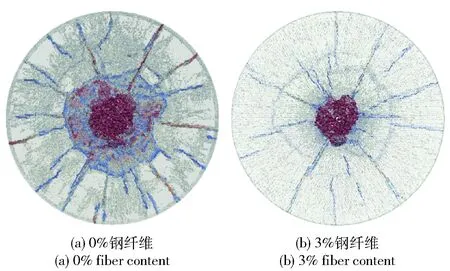
法向压缩强度满足-σbc(eD,eV)≤tN≤0,其中σbc是体应变eV相关的细观压缩边界条件,偏应变eD=eN-eV. 当压缩响应超过细观压缩强度σc0,由于基体内部孔隙坍塌,导致法向应力以较小的模量Hc随着体应变增大而增大,在ec0 压剪耦合摩擦细观剪切强度准则为σbs=σs+(μ0-μ∞)σN0[1-exp(tN/σN0)]-μ∞tN,σN0是渐近转化应力,μ0和μ∞分别是初始和渐近内摩擦系数。 基于粘聚断裂理论[18],LDPM中裂纹开裂速率相关的动态屈服准则为 (3) 其中c0和c1是混凝土材料动态参数。 2.2 纤维混凝土本构关系 当混凝土基质中掺杂纤维时,Schauffert等[19-20]认为LDPM单元某一潜在裂纹微面上力学响应σF可以理解为混凝土骨料间作用力以及穿过该微面上的耦合: (4) 式中:Ac是潜在裂纹微面的面积;pf是纤维f对裂纹的桥接作用力。 基于细观纤维拉拔响应试验与机理分析,对于图5(b)中基体内部埋深分别为Ls和Ll穿过裂纹微面纤维的桥接力pf,基于纤维拉拔机理可表示为 pf=p(v)eksnφ, (5) 式中:ksn是纤维/基体斜向作用参数;φ是埋入纤维与拔出部分夹角;p(v)是纤维相对滑移量为v对应的拉拔力, (6) 式中:vd是脱粘滑移量;Le是纤维埋入深度,其取值为Ls或Ll;df是纤维直径;β是接触系数,控制拉拔硬化或者软化响应;p0=πLedfτ0是纤维/基体最大粘结力,τ0是粘结强度。 3.1 LDPM模拟侵彻带装甲钢背板的钢纤维混凝土靶 本文采用弹塑性本构模型来模拟侵彻试验中35CrMnSiA合金弹体。Liu等[21]给出了材料参数如下:密度7.85 g/cm3,弹性模量200 GPa,泊松比0.3,屈服强度1.2 GPa. 对于装甲钢材料的本构模型,本文采用Johnson-Cook模型,这是一种考虑压力相关性、应变率强化效应和温度软化效应的理想弹塑性强化模型,其屈服准则表达式如下: (7) [13]中的高强度混凝土LDPM参数标定结果,本研究选取参数如下:等效法向弹性模量E0=72 000 MPa,切向- 法向耦合系数α=0.484,细观压缩强度σc0=500 MPa,初始硬化模量Hc0=0.36E0,渐近转化应变比κc0=2,渐近转化应力σN0=300 MPa,初始内摩擦系数μ0=0.5,渐近内摩擦系数μ∞=0,偏应变阈值比κc1=2,偏量损伤系数κc2=1,细观拉伸强度σt=4 MPa,细观剪切强度σs=17σt,拉伸特征长度lt=50 mm. 弹体与钢纤维混凝土靶、装甲钢背靶之间接触以及复合靶之间接触关系均设置为罚函数接触,其接触刚度为时间步长相关的函数,其具体表达式为 (8) 式中:mmin是发生接触的颗粒或者单元中质量最小值;Δt是显示计算步中的时间步长。罚函数接触力Fn=KsifPi,Pi是接触体相互侵入量。 3.2 复合靶侵彻仿真验证分析 利用上述LDPM和有限元建立的模型以及选定的材料参数,对带装甲钢背板的高强度钢纤维混凝土靶抗侵彻过程进行了数值模拟。并得到侵彻作用后钢纤维混凝土靶、装甲钢背靶的破坏形式如图6~图8所示。与试验现象类似,图6中仿真获得的混凝土靶体受到弹体冲击作用在弹着点附近产生破碎,伴随着辐射状裂纹。图6(b)中深红色区域表示混凝土完全破碎对应试验后混凝土靶体中心碎落部分;模型中钢纤维随机乱向分布而实际浇筑中局部纤维分布不均匀,因此仿真结果显示裂纹特征为均布的辐射状裂纹,而图6(a)中试验后混凝土圆柱靶的辐射状裂纹数量少且集中。从图7的混凝土靶体破坏的侧视图看出,仿真结果存在更多的裂纹,而试验破坏后混凝土靶的破坏更加集中。由于弹体冲击和前靶的相互作用,图8仿真结果表明装甲钢背靶迎弹面上产生开坑,这与试验现象相符。 图6 钢纤维混凝土靶破坏试验与仿真对比(俯视)Fig.6 Experimental and numerical SFRC target damages (top view) 图7 钢纤维混凝土靶破坏的试验与仿真对比(侧视)Fig.7 Experimental and numerical SFRC target damages (side view) 图8 装甲钢背靶破坏的试验与仿真对比Fig.8 Experimental and numerical steel target damages 装甲钢背靶侵彻深度的试验值和仿真预测值对比如表4所示。1号和3号实验仿真结果都是混凝土前靶刚好被弹体贯穿,在背靶没有留下明显弹坑,而2号实验由于弹体速度略大且混凝土靶略薄,仿真中穿甲弹贯穿前靶后在30 mm厚背靶上留下了8.5 mm侵彻深度,这比试验值略小。对于长杆弹侵彻情况,4号~6号实验仿真背靶侵彻深度结果约为22 mm,与试验基本一致;而侵彻96 mm厚前靶的工况,仿真结果显示背靶侵彻深度约16~17 mm,这与8号、9号实验结果吻合。 表4 复合靶侵彻仿真结果与试验结果对比Tab.4 Numerical results of composite target penetration 4.1 复合靶间隙对侵彻响应影响 带装甲钢背板的钢纤维混凝土靶抗侵彻性能除了跟侵彻体和靶体的材料相关,复合靶间是否存在间隙对于最终的抗侵彻效果也有一定的影响。本节针对仿真预测结果较好且具有代表性的3种工况(侵彻实验2号、4号和9号)分别进行含10 mm间隙条件的仿真对比分析。 如表5所示,仿真结果表明复合靶间包含间隙对于2号、4号和9号实验工况仿真背靶侵彻深度有很大影响,两层靶存在间隙时,3种工况侵彻深度分别增加了5.4 mm、6.1 mm和3.0 mm. 这是因为复合靶间存在间隙使得前靶靶背自由面在拉伸波作用下产生破坏,侵彻阻力减小。9号实验工况混凝土前靶较厚,贯穿前靶后弹体速度较小,因此对于侵彻深度影响较小。 表5 间隙对于复合靶侵彻仿真影响Tab.5 Influence of gap on numerical penetration depth 图9~图11是3种工况下,模拟不含间隙复合靶以及含间隙复合靶侵彻,靶体破坏情况的对比。从图9~图11可以看出:含间隙的情况下,前靶的靶背由于拉伸波作用产生明显的基体脱落;而背靶的迎弹面由于受到弹体挤压作用,在弹着点周围产生凸起的开坑。 图9 2号实验工况仿真有无间隙复合靶破坏对比Fig.9 Damage comparison of composite targets without/with gap in No.2 numerical test simulation 图10 4号实验工况仿真有无间隙复合靶破坏对比Fig.10 Damage comparison of composite targets without/with gap in No.4 numerical test simulation 图11 9号实验工况仿真有无间隙复合靶破坏对比Fig.11 Damage comparison of composite targets without/with gap in No.9 numerical test simulation 4.2 钢纤维含量对复合靶侵彻响应影响 本节对于纤维含量对于复合靶侵彻响应的影响进行仿真分析研究,即不同钢纤维含量的高强度混凝土靶在2号、4号和9号实验仿真中侵彻深度和混凝土靶破坏形态变化情况。0%、1%、2%和3%体积含量钢纤维高强度混凝土靶板,不同侵彻工况下背靶侵彻深度的仿真计算结果如表6所示。从表6可以看出,3%体积含量以内钢纤维对于复合靶侵彻的背靶侵彻深度几乎没有影响。 表6 钢纤维对于复合靶侵彻仿真影响Tab.6 Influence of fiber on numerical penetration depth 图12 4号实验工况仿真钢纤维含量对于混凝土靶破坏对比Fig.12 Damage results of concrete targets with various fiber contents in No.4 numerical test simulation 由于钢纤维能够桥接裂纹并阻止其扩展,所以不同钢纤维混凝土侵彻仿真靶体破坏情况和裂纹分布值得进一步分析。如图12所示,仿真结果显示随着钢纤维含量的增加开坑面积显著减小,且径向的辐射状裂纹也逐渐减少。因此可以判断钢纤维的桥接作用使得混凝土材料冲击破坏区域更加集中在侵彻隧道附近,其附近的材料受到较小的破坏和损伤。这对多次冲击问题具有非常重要的借鉴意义。 随着纤维混凝土的迅速发展和应用,钢纤维混凝土靶板抗侵彻的防护性能研究具有重要的意义。针对前文钢纤维混凝土复合靶的仿真研究,本研究进一步对靶体尺寸和钢纤维等因素对于弹体冲击钢纤维混凝土板贯穿响应影响因素进行仿真分析。分别选取不同截面尺寸、厚度尺寸的高强度钢纤维混凝土圆柱靶以及不含钢纤维的混凝土靶,进行不同撞击速度的侵彻贯穿仿真。靶体侧面施加轴向位移约束,允许靶体径向膨胀但不能发生弹体正侵彻冲击方向的位移。 5.1 靶板直径对出靶速度影响 对于有限靶贯穿问题,圆柱形靶板的截面尺寸对出靶的剩余速度会有一定的影响。当靶体直径较小时冲击产生的裂纹扩展到达侧面自由端,靶体发生散裂;而当靶板直径足够大时,靶体受到冲击的裂纹扩展不能够达到侧面边界,此时侧面自由边界对于侵彻响应影响可以忽略。两种情况下侵彻阻力的变化导致不同的贯穿响应,进而影响弹体出靶剩余速度。 图13 不同直径尺寸钢纤维靶受到卵形弹体823 m/s速度撞击破坏对比Fig.13 Damage modes of SFRC targets with different diameter subjected to 823 m/s projectile impact 图13对比仿真获得的穿甲弹贯穿100 mm直径和400 mm直径高强度钢纤维混凝土圆柱靶破坏情况,从中可以看出裂纹分布在整个100 mm直径的靶体,而400 mm直径靶体由于截面较大,弹着点远处区域并未发生开裂现象。 为了研究圆柱靶截面直径尺寸对于弹体贯穿后出靶剩余速度的影响,本文对穿甲弹以823 m/s着靶速度正侵彻厚度为50 mm,直径分别为100 mm、120 mm、160 mm、200 mm、240 mm、300 mm、360 mm以及400 mm的高强度钢纤维混凝土靶体进行LDPM模拟分析,出靶速度结果对比如图14所示。随着靶板直径的增大,弹体剩余速度呈现跳跃式的降低趋势,直到靶板直径达到300 mm左右,出靶速度趋于稳定。靶板直径大于300 mm的工况,由于LDPM离散元模型单元随机性,出靶速度随着靶体直径尺寸变化规律带有跳跃性。 图14 823 m/s速度贯穿不同直径尺寸的靶体后出靶速度对比Fig.14 Residual velocities for plates with different diameter perforated at 823 m/s 5.2 靶板厚度与贯穿响应关系 基于前文结论,本节选择靶体直径为300 mm,厚度分别为20 mm、30 mm、40 mm和50 mm,仿真研究高强度钢纤维混凝土靶板厚度对穿甲弹、长杆弹贯穿响应的影响。 图15是穿甲弹贯穿20 mm和40 mm厚靶体后靶体内部破坏情况,从中可以看出:20 mm厚靶板破坏区域裂纹更多,且开坑区域附近的混凝土在弹体冲击作用下产生向靶后运动趋势;而40 mm厚靶体结构未发生破坏,剖视图显示靶体内部明显的开坑和隧道区。 图15 不同厚度靶贯穿后的破坏Fig.15 Damage modes of different thick plates 为了定量描述有限厚度靶贯穿特性,本文采用Lambert-Jonas经验公式[23]对弹体出靶剩余速度vr和撞击速度vs的关系进行构建: (9) 式中:vbl是弹道极限速度;p是用来拟合曲线的经验参数。 图16和图17分别给出了穿甲弹和长杆弹贯穿300 mm直径不同厚度高强度钢纤维混凝土靶板的出靶速度情况。对于穿甲弹侵彻20 mm、30 mm、40 mm和50 mm厚高强度钢纤维混凝土靶体,剩余速度和撞击速度几乎呈现直线关系,结合(9)式其拟合结果值分别为1.19、1.24、1.28和1.31. 而长杆弹贯穿4种厚度钢纤维混凝土靶板剩余速度与撞击速度关系拟合值分别为1.42、1.50、1.52和1.59. 图16 穿甲弹贯穿不同厚度靶响应Fig.16 Perforation responses of armor-piercing projectiles penetrating different thickplates 图17 长杆弹贯穿不同厚度靶响应Fig.17 Perforation responses of long rod projectiles penetrating different thick plates 5.3 钢纤维含量对贯穿响应影响 为了探究不同撞击速度工况下,钢纤维对于冲击响应的影响,本节选择20 mm厚、300 mm直径混凝土靶体进行仿真研究。对比无钢纤维和3%体积含量钢纤维的混凝靶板受到穿甲弹冲击贯穿响应。仿真结果表明无钢纤维的靶板出现较大的裂纹开裂以及靶背崩落开裂区域,而3%体积含量的钢纤维混凝土靶背由于钢纤维的桥接作用,裂纹较少且崩落区域远远小于无钢纤维靶板,如图18所示。 图18 钢纤维含量对于混凝土靶板贯穿破坏影响Fig.18 Effect of fiber on target perforation damage 结合Lambert-Jonas经验公式,穿甲弹贯穿无钢纤维以及含3%钢纤维的混凝土靶板后的剩余速度与不同撞击速度关系如图19所示。弹体贯穿仿真结果表明:弹体撞击速度接近弹道极限速度时,3%体积含量钢纤维才对剩余速度产生较明显影响。这是因为侵彻阻力主要与速度相关的惯性效应以及靶体材料强度相关,当侵彻速度较低时,掺杂钢纤维对于材料增强效果才会对侵彻阻力产生较明显作用。 图19 钢纤维对于穿甲弹贯穿混凝土靶响应的影响Fig.19 Effect of fiber on perforation response 通过侵彻带装甲钢背板的高强度钢纤维混凝土靶试验,本文结合防护系数评估了复合靶的抗侵彻性能。基于LDPM细观离散元模型,研究建立了钢纤维混凝土靶侵彻的数值仿真模型,成功预测背靶侵彻深度并较好地描述混凝土破坏形态。对不同影响因素侵彻工况仿真分析表明: 1)相比含间隙的复合靶,无间隙的约束条件能够增强侵彻阻力,明显减小背靶侵彻深度;相同弹体撞击速度时,前靶越厚,间隙对于侵彻深度的影响越小。 2)本文选用的钢纤维混凝土材料其钢纤维体积含量在3%以内时,背靶侵彻深度几乎没有影响,而混凝土靶破坏形态变化明显。 3)对于本文研究的3%钢纤维体积含量的混凝土靶,圆柱靶直径大于30倍弹径时,弹体贯穿出靶速度趋于收敛。仿真穿甲弹侵彻300 mm直径钢纤维混凝土靶,当厚度分别为20 mm、30 mm、40 mm和50 mm时,剩余速度与撞击速度关系Lambert-Jonas经验公式拟合p值分别为1.42、1.50、1.52和1.59. 参考文献(References) [1] Feng J, Sun W W, Wang X M, et al. Mechanical analyses of hooked fiber pullout performance in ultra-high-performance concrete[J]. Construction & Building Materials, 2014, 69(11):403-410. [2] 吴莹, 吴永东, 钟伟芳. 利用SMA拟弹性增强复合材料梁抗低速冲击性能[J]. 华中科技大学学报:自然科学版, 2008, 36(11):112-115. WU Ying, WU Yong-dong, ZHONG Wei-fang. Improvement the low velocity impact performance of composite beam by using the pseudo-elastic effect of SMA[J]. Journal of Huazhong University of Science & Technology:Natural Science Edition, 2008, 36(11):112-115. (in Chinese) [3] 孙巍巍, 董浩林, 高旭东,等. 混杂纤维增强水泥基复合材料力学性能研究[J]. 混凝土与水泥制品, 2015(8):49-52. SUN Wei-wei, DONG Hao-lin, GAO Xu-dong, et al. Mechanical investigations on hybrid fiber reinforced cement composite materials[J]. China Concrete and Cement Products, 2015(8):49-52.(in Chinese) [4] 纪冲, 龙源, 方向,等. 基于FEM-SPH耦合法的弹丸侵彻钢纤维混凝土数值模拟[J]. 振动与冲击, 2010, 29(7):69-74. JI Chong, LONG Yuan, FANG Xiang, et al. FEM-SPH coupling numerical analysis of projectile penetration in steel fiber reinforced concrete[J]. Journal of Vibration and Shock, 2010, 29(7):69-74. (in Chinese) [5] 董新龙, 洪志权, 高培正,等. 混凝土及钢纤维混凝土板爆炸破坏研究[J]. 兵工学报, 2009,30(增刊2):280-283. DONG Xin-long, HONG Zhi-quan, GAO Pei-zheng, et al. Study on collapse of common and steel fiber reinforced concrete slabs subjected to contact detonation[J]. Acta Armamentarii, 2009,30(S2):280-283. (in Chinese) [6] 刘志林,孙巍巍,王晓鸣,等. 基于盖帽模型的混凝土动态球形空腔膨胀模型和侵彻阻力分析[J]. 兵工学报,2015, 36(12): 2209-2216. LIU Zhi-lin, SUN Wei-wei, WANG Xiao-ming, et al. Spherical cavity-expansion model for concrete targets based on cap model and penetration resistance analysis[J]. Acta Armamentarii, 2015, 36(12): 2209-2216. (in Chinese) [7] 刘桂武, 倪长也, 金峰,等. 陶瓷/金属复合装甲抗弹约束效应述评[J]. 西安交通大学学报, 2011, 45(3):7-15. LIU Gui-wu, NI Chang-ye, JIN Feng, et al. Review of anti-ballistic confinement effects of ceramic-matal composite armor[J]. Journal of Xi’an Jiaotong University, 2011, 45(3):7-15. (in Chinese) [8] Forrestal M J, Tzou D Y. A spherical cavity-expansion penetration model for concrete targets[J]. International Journal of Solids and Structures, 1997, 34(31): 4127-4146. [9] Feng J, Li W, Wang X, et al. Dynamic spherical cavity expansion analysis of rate-dependent concrete material with scale effect [J]. International Journal of Impact Engineering, 2015, 84: 24-37. [10] Kirane K, Su Y, Bažant Z P. Strain-rate-dependent microplane model for high-rate comminution of concrete under impact based on kinetic energy release theory[J]. Proceeding of the Royal Society of London A, 2015, 471(2182): 20150535. [11] Cusatis G, Pelessone D, Mencarelli A. Lattice discrete particle model (LDPM) for failure behavior of concrete. I: theory[J]. Cement and Concrete Composites, 2011,33(9): 881-890. [12] Cusatis G, Mencarelli A, Pelessone D, et al. Lattice discrete particle model (LDPM) for failure behavior of concrete. II: calibration and validation[J]. Cement and Concrete Composites, 2011,33(9): 891-905. [13] Smith J, Cusatis G, Pelessone D, et al. Discrete modeling of ultra-high-performance concrete with application to projectile penetration[J]. International Journal of Impact Engineering, 2014,65: 13-32. [15] Jin C, Buratti N, Stacchini M, et al. Lattice discrete particle modeling of fiber reinforced concrete: experiments and simulations[J]. European Journal of Mechanics-A/Solids, 2016, 57(1/2): 85-107. [16] Cusatis G, Schauffert E. Discontinuous cell method (DCM) for cohesive fracture propagation[C]∥Korea Concrete Institute. Proceedings of the 7th International Conference on Fracture Mechanics of Concrete and Concrete Structures. Jeju: Korea Concrete Institute, 2010: 23-28. [17] Rezakhani R,Cusatis G. Asymptotic expansion homogenization of discrete fine-scale models with rotational degrees of freedom for the simulation of quasi-brittle materials[J]. Journal of the Mechanics and Physics of Solids, 2016, 88: 320-34. [18] Cusatis G. Strain-rate effects on concrete behavior[J]. International Journal of Impact Engineering, 2011, 38(4):162-170. [19] Schauffert E A, Cusatis G. Lattice discrete particle model for fiber-reinforced concrete. I: theory[J]. Journal of Engineering Mechanics, 2011, 138(7): 826-833. [20] Schauffert E A, Cusatis G, Pelessone D, et al. Lattice discrete particle model for fiber-reinforced concrete. II: tensile fracture and multiaxial loading behavior[J]. Journal of Engineering Mechanics, 2011, 138(7): 834-841. [21] Liu Y, Huang F, Ma A. Numerical simulations of oblique penetration into reinforced concrete targets[J]. Computers & Mathematics with Applications, 2011, 61(8): 2168-2171. [22] Banerjee A, Dhar S, Acharyya S, et al. Determination of Johnson cook material and failure model constants and numerical modelling of Charpy impact test of armour steel[J]. Materials Science and Engineering: A, 2015, 640: 200-209. [23] Lambert J P, Jonas G H. Towards standardization in terminal ballistics testing: velocity representation[R]. Aberdeen, Maryland, US:Army Ballistic Research Lab, Aberdeen Proving Ground MD, 1976. Experiments and Numerical Simulation of Penetration Resistance ofSteel Fiber Reinforced Concrete Target Backed by Steel Plate FENG Jun1,2, SUN Wei-wei3, LIU Zhi-lin2, WANG Xiao-ming2 (1.National Key Laboratory of Transient Physics, Nanjing University of Science & Technology, Nanjing 210094, Jiangsu, China;2.School of Mechanical Engineering, Nanjing University of Science & Technology, Nanjing 210094, Jiangsu, China;3.School of Science, Nanjing University of Science & Technology, Nanjing 210094, Jiangsu, China) In order to investigate the penetration resistance of steel fiber reinforced concrete (SFRC), 12.7 mm armor-piercing projectiles and long rod projectiles are used to penetrate a high strength fiber reinforced concrete backed by armor steel in high speed impact test. The penetration resistance of composite target is evaluated using protection factor according to the penetration depth of rear target. The lattice discrete particle model (LDPM) is introduced to model fiber reinforced concrete, and the elastic-plastic model and Johnson-Cook criterion are used to describe the projectile and armor steel. A numerical simulation model for penetration into concrete target is established. The feasibility of numerical model for simulation of penetration into fiber reinforced concrete is validated in terms of penetration depth and concrete target damage mode. The effects of internal gap and fiber content of composite target on penetration response in 3 typical penetration tests are simulated and analyzed. The numerical results show that, for the composite target without gap, the residual penetration depth of rear target can be effectively reduced, and the fiber reinforcement has no effect on the penetration depth but affects the concrete damage mode significantly. Further numerical analyses of fiber reinforced concrete target perforated by 12.7 mm armor-piercing projectiles indicate that the perforation velocity of projectile tends to converge if the diameter of cylindrical target is 30 times larger than projectile diameter, and the residual velocity approximates a linear relationship with impact velocity with the decrease in target thickness. ordnance science and technology; fiber reinforced concrete; penetration resistance; numerical modeling; perforation response 2016-11-28 国家自然科学基金项目(11602111); 中央高校基本科研业务费专项资金项目(30917011343) 冯君(1988—),男,讲师,博士。E-mail: jun.feng@njust.edu.cn 孙巍巍(1979—),男,副教授,硕士生导师。E-mail: sww717@163.com O385 A 1000-1093(2017)06-1041-11 10.3969/j.issn.1000-1093.2017.06.001



3 数值模拟复合靶抗侵彻试验





4 仿真分析复合靶抗侵彻影响因素




5 钢纤维混凝土板贯穿响应仿真


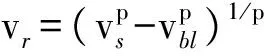



6 结论

