中国十大城市房价泡沫相依结构及其传导机制研究

郭文伟

一、引言

2015年在国家去库存、支持刚需和改善型需求的宏观调控政策影响下,中国房地产市场整体持续复苏。来自国家统计局的数据显示:2015年70个大中城市一、二手住宅价格分别同比增长了7.7%和7.6%；相比之下,四个一线城市 (深圳、上海、北京、广州)尤其是深圳的一、二手房价格涨幅则大幅领先其他城市；其中,在一手房方面分别涨了47.5%、18.2%、10.4%、9.2%,在二手房方面分别上涨了42.6%、20.8%、11.7%和11.7%。进入2016年以来,中国房地产市场价格走势两极分化现象进一步加重,这主要表现在:一方面,北京、上海、广州、深圳这些一线大城市房价依然延续2015年的上涨态势,并带动部分二线重点城市 (天津、重庆、南京、杭州、武汉、成都)房价随之上涨,有些城市涨幅甚至远超一线城市。与此同时,高总价、高地价、高溢价的“三高地块”屡屡出现在这十大城市中,“地王”现象和“日光盘”现象不断出现,无不显示出这些大城市房地产市场供求两旺与“豪宅化”趋势特征。另一方面,众多三、四线中小城市却面临库存高压、市场观望情绪浓重、房价调整趋势加重的局面。由此可见,我国房地产市场的结构性失衡程度在持续加重；一、二线城市房价的快速上涨不但加剧了三、四线城市去库存的难度和压力,扭曲了经济结构,而且也强化了房价上涨预期,推高了整个社会的生活和生产成本,并降低了生产效率,严重制约着我国创新驱动发展战略的顺利实施。目前,社会各界对我国一、二线大城市的高房价问题高度关注,在是否存在房价泡沫及其泡沫严重程度上尚存争议,但普遍认为一旦房价全面大幅下跌,严重时将会引发系统性金融风险。因此,防范房价泡沫破灭及其引发的各类风险就成了各级政府不得不面临的重要问题。有效防范房价泡沫破灭风险的关键在于对房价泡沫存在性、存续周期时点、演化趋势及其相互传导机制具有科学合理的认识。对此,本文首次通过构建资产泡沫动态监测方法来刻画国内十大城市一、二手住宅价格泡沫的演化过程；在全面比较各城市房价泡沫程度的基础上,采用R-Vine Copula模型来构建这十大城市房价泡沫的相依结构,进而结合格兰杰因果关系检验法揭示各城市房价泡沫的传导机制。本文研究意义在于:一方面,通过揭示国内十大城市住宅价格泡沫的演化过程,能帮助政府监管层及时把握国内热点城市住宅泡沫的动态趋势,为其制定有效的房价泡沫抑制措施提供支持；另一方面,通过揭示十大城市房价泡沫之间形成的相依结构及传导机制,增强防范各城市房价泡沫交叉传染等措施的科学性和合理性。

二、文献综述

国外学者主要基于三类方法来对房价泡沫存在性进行检测:第一类是综合指标法。该方法通过合成某种综合指标来衡量房价泡沫程度,常见的综合指标有租售比、房价收入比、空置率、房地产贷款与国内生产总值比率等,通过将国内这些综合指标与国外相应指标进行比较来判断是否存在房价泡沫及其严重程度。整个分析过程虽然易于操作,但在综合指标合成过程中存在较大主观性,比如采取哪些子指标及其权重如何确定等问题,而且这类方法只能判断是否存在泡沫及其相对严重程度,并不能判断泡沫的存续周期时点。第二类是基于单位根检验的泡沫识别方法。Phillips等 (2011)［1］率先提出结合单位根右侧检验和向前移动窗口递归技术的资产泡沫监测方法SADF(Sup ADF test,SADF),但这类方法仅能监测到一个周期性泡沫,而无法同时检测出可能存在的多个周期性泡沫；同年,Phillips和 Yu(2011)［2］采用 SADF方法对美国房地产市场进行实证研究,发现美国在2002年5月至2007年12月出现了明显的房价泡沫,而且随后房价泡沫的破灭引发了次贷危机。Chen和Funke(2013)［3］采用SADF方法对中国房地产市场2003—2011年的房价走势进行检验,结果发现中国房地产市场除了2009年10月出现明显的房价泡沫外,其他时期均无泡沫。Yiu等 (2013)［4］同样运用SADF模型对香港房地产市场的泡沫存在性进行检验,研究结果表明:香港的普通住宅市场和豪宅市场在1995年、1997年、2004年和2008年均出现明显泡沫,其中以1997年出现的房价泡沫最为显著；而在2011年早期,香港的普通住宅 (中小户型)市场再次出现泡沫,但豪宅市场却不存在泡沫。Kivedal(2013)［5］同样采用类似方法对美国房地产市场泡沫进行实证研究。针对SADF方法的局限,Phillips等(2015a,2015b)［6－7］提出了 BSADF 方法 (Backward Sup ADF test,BSADF),该方法进一步引入可向前(后)的移动窗口递归技术,能一次性检测到可能存在的多个周期性泡沫。Engsted等 (2016)［8］采用BSADF方法来分析18个经合组织国家1970—2013年的房价泡沫,与此同时,将分析结果与 Engsted和Nielsen(2012)［9］提出的 co-explosive VAR 方法分析结果进行比较；其研究结果表明,在大部分经合组织国家明显存在房价泡沫。第三类是其他综合类方法。Zhou和Sornette(2006)［10］采用物理金融模型对美国50个州的房地产市场泡沫进行检测,最终发现有22个州显著存在房价泡沫,而且这些房价泡沫大都集中在美国西部和东北部,美国总体房价泡沫在2006年中期出现破灭的拐点。Zhou和Sornette(2008)［11］采用同样方法分析了拉斯维加斯27个城市1983—2005年的房价泡沫存在性,其研究结果表明大部分地区存在房价泡沫。Chang等 (2012)［12］研究了新加坡住宅市场1996—2010年房价走势及其变化率,然后基于聚类分析方法来探测是否存在房价泡沫。Caspi(2015)［13］采用动态高登成长模型 (Dynamic Gordon Growth Model)结合以色列的房价租金比数据来分析该国层面和地区层面上的房价泡沫程度,其研究结果表明以色列全国层面与地区层面的房价泡沫程度不一致。

在国内,由于各学者采取不同的房价泡沫定义及检测方法,导致在是否存在泡沫及其严重程度等方面的研究结论出现明显差异。目前国内主要出现四种代表性的房价泡沫检测方法。第一种是基于综合指标的房价泡沫检测方法。李维哲和曲波 (2002)［14］提出了一种房地产泡沫的预警综合指标,该综合指标包含了四大类子指标:金融类指标、交易类指标、生产类指标和消费类指标。该预警指标的构建思路依然依赖于房地产景气的测度,而且包含的子指标太多,在实践应用中存在操作不方便等问题。吕江林 (2010)［15］针对我国房地产市场实际情况,经过系统性分析后认为传统房价泡沫判定指标 (诸如租售比、空置率、投资购房与自住购房之比、房地产贷款占比和房地产业利润率等)无法有效揭示出国内房价泡沫,并认为国内城市间泡沫程度差异较大。第二种是基于局部均衡模型的房价泡沫检测方法。周京奎和曹振良(2004)［16］采用该方法来对房地产市场进行实证研究,其研究结论认为当时的中国房地产业并不存在投机泡沫。姜春海 (2005)［17］重新定义了房地产基本价值、投机泡沫和泡沫度,同样采用该方法来对国内楼市进行实证分析,最终发现国内房地产市场存在严重的泡沫。苑德宇和宋小宁 (2008)［18］通过计算我国35个大中城市2001—2005年的均衡价格与其平均价格的偏差来衡量城市房价泡沫,其研究结果表明:城市高房价不等于高泡沫,国内房价泡沫存在区域性差异和区域性传染效应。吕炜和刘晨晖 (2012)［19］采用类似方法对国内31个省份的房价泡沫进行测度,研究结果发现国内不同省份的房价泡沫存在显著差异。范新英等 (2013)［20］在综合考虑经济基本面和心理预期因素影响的基础上,利用我国35个大中城市房价构建了动态面板数据模型,借助迭代回归方法计算均衡价格,通过计算实际房价与均衡价格的偏差来测度房价泡沫。其研究结论表明近几年我国大多数城市房价泡沫有加大趋势,但不同城市之间房价泡沫程度差异较大。第三种是基于West模型的房价泡沫检测方法。韩德宗 (2005)［21］认为房地产合理价格是租金的资本化,应用West模型来检验国内北京、上海和深圳房价泡沫的存在性,研究结果表明:这三个一线城市的住宅市场均存在房价泡沫,而其写字楼市场均不存在房价泡沫。West模型同样存在无法明确泡沫存续周期时点的局限。第四种是基于马尔可夫区制转换模型的房价泡沫检测方法。王春雷 (2008)［22］利用 Norden(1996)［23］较早提出的基于马尔科夫区制转换的泡沫检验方法进行实证,结果发现国内房地产市场存在短期泡沫。史兴杰和周勇 (2014)［24］在放宽 Norden(1996)［23］所提出模型假设的基础上,提出了更为有效的区制转换自回归模型来分析国内直辖市的房价泡沫,结果发现北京和上海的房价泡沫显著,天津和重庆的房价泡沫不明显。

总的来看,在房价泡沫监测方法上,国内学者已先后提出了综合指标法、局部均衡模型识别法、West模型、区制转换自回归模型等房价泡沫检测方法。然而现有房价泡沫检测方法主要存在几个问题:第一,只能判断是否存在泡沫 (综合指标法、局部均衡模型),而无法揭示泡沫的存续周期时点。第二,只能揭示单个泡沫及其存续周期时点而无法揭示出可能存在的多个泡沫 (SADF、West模型)及其存续周期。第三,能揭示出多个泡沫,但无法区分不同泡沫的异质性特征 (BSADF、马尔可夫区制转换模型)。总的来看, 在这些方法中,Phillips等 (2015a,2015b)［6－7］提出BSADF方法具有明显优势:第一,该方法能一次揭示出整个研究时期内可能存在的多个周期性泡沫。第二,该方法只依赖于房价指数来进行房价泡沫测度,从而回避了涉及房价基本面或基础价值方面的主观判断,使得各区域房价泡沫的测度具有统一性和可比性。第三,能充分展示每个时点上的房价泡沫值及其动态变化过程。因此,本文先采用BSADF方法对中国十大城市一、二手房价泡沫进行动态监测,在此基础上,鉴于各大城市房价泡沫之间可能存在相依性,采用新近发展起来的R-Vine Copula方法来构建这十大城市的房价泡沫相依结构,进而分析各城市房价泡沫之间可能存在的非线性、非对称的复杂相依结构特征,并结合格兰杰因果关系检验法来揭示各城市房价泡沫之间的传染机制。相比现有研究,本文的特色在于:第一,首次基于BSADF方法动态测度了国内十大城市一、二手住宅在研究时期内的价格泡沫程度、存续周期和演化过程。第二,引入R-Vine Copula方法来构建国内十大城市一、二手住宅价格泡沫的高维相依结构,揭示出各大城市房价泡沫之间的相依性具有非线性、非对称的特征。第三,揭示出各城市房价泡沫的相互传染机制。显然,这些研究将为制定防范房价泡沫破灭及向外传染的有效监管措施提供有益的借鉴。

三、房价泡沫及其相依结构模型的构建

(一)房价泡沫测度模型:BSADF方法

由于基于协整检验原理来判断资产泡沫存在性的传统方法无法有效挖掘周期性泡沫,对此,Phillips等 (2011)［1］提出了具有弱爆炸过程特征的周期性泡沫检验方法 (简称SADF),该方法通过检验资产价格走势的ADF检验模型中自回归系数ρ是否显著大于1来挖掘泡沫的存续周期:

当资产价格走势过程中ρ≤1时表示处于无泡沫状态,而当ρ＞1时表示处于泡沫阶段状态。SADF同样采用向前移动窗口递归技术,具体做法为:先确定固定窗口长度和步长的样本数据pt(t＝1,2,…,［Tr］,0＜r＜1,［·］表示取整)； 然后利用这些数据对公式 (1)进行参数估计,在获得参数ρ的t统计量后,向前移动一个步长获得新的样本数据后再进行参数估计,直至样本全部用完；最后将能获得ρ的ADF统计量序列。这些序列的上确界将视为SADF值:

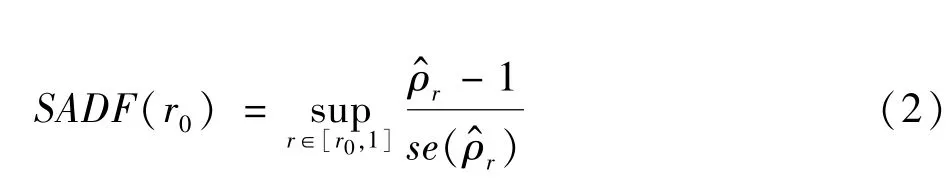
资产泡沫的存续周期时点判断原则如下:

其中,为在100βT%置信水平上、样本容量为 ［Tr2］情况下的SADF临界值。表示泡沫发生时点,表示泡沫消失时点。［27］

(二)房价泡沫相依结构模型:R-Vine Copula方法

在构建高维Copula模型方面,先后共出现了三种代表性方法:C-Vine Copula、D-Vine Copula(Bedford 和 Cooke,2001［25］)、 R-Vine Copula(Dißmanna等,2013［26］)。其中, 前面 C-Vine Copula和 D-Vine Copula模型一般称为正则藤建模方法,是后面一般化R-Vine Copula模型的特例。R-Vine Copula不需要事先设定其树结构形式,没有特定的树结构形式和分解规则,可以随时根据变量间的相依性或研究目的需要来安排其相依结构形式,突显出极大的灵活性和实用性 (郭文伟,2016［27］)。Dißmanna 等 (2013)［26］的研究结果也表明,R-Vine Copula方法比C-Vine Copula和D-Vine Copula方法的分析结果更稳健。目前国内采用R-Vine Copula来对资产泡沫之间的相依结构进行建模分析的文献较少,仅仅有郭文伟 (2016)［27］采用该模型对全球21个代表性股市泡沫之间的相依结构特征进行实证分析,但尚未有文献专门对国内十大城市一、二手房价泡沫之间的相依结构进行建模分析,对此,本文采用R-Vine Copula模型来分析国内十大城市一、二手房价泡沫之间的相依结构特征。由于文章篇幅限制,有关R-Vine Copula模型的结构形式和原理等方面的内容,可详见上述文献,这里不再阐述。

四、国内十大城市房价泡沫测度及其相依结构分析

(一)十大城市房价指数的选取与说明

本文基于城市经济规模、人口规模和各城市一手住宅、二手住宅价格指数可获性的原则,最终选择了中国内地十大城市 (北京、上海、广州、深圳、天津、杭州、南京、武汉、重庆、成都)①本文所选取的十大城市与近几年国内流行的十大城市名单并不完全一致,这里没有将近3年一直入围国内十大城市行列的苏州市纳进来,主要原因是由于苏州市各层次房价指数的历史数据较短,且不容易获得。。所有数据来源于Wind资讯,房价指数均为月度数据。由于每个城市的一、二手住宅价格指数的时期起点并不完全一致,因此,为了全面揭示这十大城市一、二手住宅价格泡沫的全周期演化过程,这里对各个城市房价指数单独进行分析,不统一时间起点,只统一时间终点；这是因为一旦统一研究时期起点,有可能会漏掉个别城市在被剪切掉的时期内出现的周期性泡沫。各城市研究时期如表1所示。

表1 十大城市各层次房价指数的研究时期

表2给出这十大城市房价指数在各自研究时期内的描述性统计结果；从表2中可知:十大城市一、二手房价指数均表现出轻微的左偏或右偏的分布特征,但并不具有尖峰的分布特征。所有城市的一、二手房价指数的JB统计值均在5%的置信水平上拒绝原假设,说明所有房价指数均不服从正态分布。从房价指数标准差来看,无论是一手房还是二手房,北京、深圳、上海、广州的标准差依次最大,说明一线城市的一、二手房价波动程度要大于其他二线城市,相比之下,成都的一、二手房价波动程度在十大城市中最小。

表2 十大城市一、二手住宅价格指数描述性统计结果

续前表

(二)十大城市房价泡沫存在性检验

这里同时采用SADF和BSADF检验法来检测国内十大城市一、二手住宅价格泡沫,最终检测结果如表3所示。首先假定移动窗口的初始长度为6个月,步长为1个月来进行递归分析；然后每次往前移动窗口新增一个月的样本数据进行循环估计；最后进行了2 000次模拟来获得资产泡沫在1%、5%和10%置信水平上的临界值系列。从检验结果可知:在三种置信水平上,除了北京和深圳的BSADF统计值与SADF统计值相等外,其他城市的BSADF统计值均明显大于SADF统计值,说明BSADF检验法能发现SADF检验法无法检测到的资产价格周期性泡沫。在一手房方面,北京、广州、深圳、天津、杭州、南京、武汉的BSADF统计值均显著大于其在1%置信水平上的临界值,说明在1%的置信水平上,这7个城市的一手住宅价格均在研究时期内显著存在周期性泡沫。重庆、成都的BSADF统计值均显著大于其在5%置信水平上的临界值,说明在5%的置信水平上,这2个城市的一手住宅价格均在研究时期内显著存在周期性泡沫。而上海的BSADF统计值大于其在10%置信水平上的临界值,说明在10%的置信水平上,上海一手住宅价格存在周期性泡沫。在二手房方面,北京、广州、重庆、天津、杭州、南京、武汉、成都的BSADF统计值均显著大于其在1%置信水平上的临界值,说明在1%的置信水平上,这8个城市的二手住宅价格均在研究时期内显著存在周期性泡沫。上海、深圳的BSADF统计值均显著大于其在5%置信水平上的临界值,说明在5%的置信水平上,这2个城市的二手住宅价格均在研究时期内显著存在周期性泡沫。总体上看,国内十大城市一、二手住宅均在各自的研究时期内出现周期性泡沫。

表3 十大城市房价指数基于SADF和BSADFS的检验结果

续前表

(三)十大城市房价泡沫存续周期时点及其泡沫程度比较

由于文章篇幅限制,这里不再一一给出各城市一手和二手房房价泡沫的走势图,仅对每个城市在整个研究时期内出现的泡沫次数、最长泡沫周期及最严重泡沫程度进行汇总对比,具体结果见表4。从表4可知,无论是一手房还是二手房,国内十大城市均出现多次周期性房价泡沫,但在泡沫的严重程度、发生次数和持续周期上均存在显著差异。

表4 十大城市房价泡沫统计汇总

在一手房方面,从各城市房价泡沫均值来看,从大到小依次是:北京＞上海＞深圳＞南京＞广州＞天津＞杭州＞武汉＞成都＞重庆。其中,北京、上海和深圳这三个一线城市的房价格泡沫最为严重,而重庆的房价泡沫程度最小。与此同时,国内四大一线城市的房价泡沫总体上要明显大于其他二线城市的房价泡沫。在泡沫峰值及其存续周期方面,北京在2007年11月出现了最严重且持续时间最长的泡沫,泡沫峰值高达16.34；这次泡沫从2006年2月开始出现至今尚未破灭,持续时间长达10年以上。与此类似,上海也在2002年12月出现了持续时间长达10年的泡沫,直到2012年11月该泡沫才消失；与此同时,上海在2013年10月出现了最严重的泡沫,泡沫峰值达到6.99。南京、杭州、广州、深圳这四个城市也曾出现较为严重的房价泡沫 (泡沫峰值分别为 10.86、10.2、8.68、8.44),最长泡沫持续时间均为2.5年左右。相比之下,重庆出现的房价泡沫次数、泡沫峰值和泡沫持续时间在十大城市中为最小,说明重庆的一手住宅市场价格泡沫相对并不严重。

在二手房方面,从各城市房价泡沫均值来看,从大到小依次是:北京＞广州＞上海＞深圳＞重庆＞天津＞南京＞武汉＞杭州＞成都。其中,北京的二手房价格泡沫依然最为严重；变化最大的是重庆,其一手房价格泡沫程度最小,但在二手房价格泡沫排行榜中位居第五,说明重庆的二手房市场价格泡沫要明显大于其一手房市场。成都的一、二手房房价格泡沫在十大城市中分别位列第九位和第十位,这说明成都房价泡沫在这十大城市中是相对较小的。作为一线城市的广州和深圳的二手房价泡沫在国内十大城市房价泡沫排名中分列第二和第四位。在泡沫峰值及其存续周期方面,北京在2007年11月出现了最严重泡沫 (泡沫峰值为9.73),在2009年8月至2011年8月期间出现了持续时间最长的泡沫,共持续了25个月。上海、广州、深圳的二手房价格泡沫程度较为接近；北京、上海、广州均在2007年下半年出现最严重泡沫；而深圳则在2016年上半年出现最严重泡沫,显然,这与自2015年下半年以来,深圳二手房价格涨幅大幅领先国内其他城市具有一定的关系。在二线城市中,重庆的二手房价价格泡沫最为严重,其在2009年9月至2012年2月出现了持续时间长达30个月的泡沫,并在2013年10月出现了最严重的泡沫 (泡沫峰值达到11.3)；相比之下,武汉和成都的房价泡沫峰值及其持续时间均较小。

从一、二手住宅层面比较来看,国内十大城市一手住宅价格泡沫程度要明显大于二手住宅价格泡沫,但在具体城市上存在结构性差异。其中,北京、上海、深圳、杭州、南京、成都这些城市的一手房价格泡沫要比其二手房价格泡沫严重；而广州、天津、重庆、武汉这些城市的一手房价价格泡沫要小于其二手房价格泡沫。一线城市最严重房价泡沫主要发生在2007年期间,而二线城市最严重泡沫主要发生在2013年和2016年,由此可见,国内大城市房价泡沫已经由一线城市向部分重点二线城市扩散和蔓延了。

(四)十大城市房价泡沫相依结构特征

本文以国内十大城市房价泡沫为研究对象,对应维度d＝10,则R-Vine Copula模型在理论上有2d－1＝29＝512个结构不同的RVM矩阵。为了从中选出最合适的RVM矩阵,本文采用Dißmanna等 (2013)［18］提出的最大生成树方法来进行选择。该方法基于最强相依关系对构建R-Vine Copula模型的重要性原则来构造每两个节点间的相依性绝对值之和达到最大的第一棵树。有关该方法的详细介绍可见文献。［18］在确定好最佳的RVM矩阵后,基于AIC和BIC值最小、对数似然值LL最大的原则从31种备选Copula模型中选出合适的函数类型来分析任意相连的节点之间的相依性。在程序算法上,这里参考了 Dißmanna等(2013)［18］提出的算法,用R语言编程来完成内部Copula类型的选取与Copula模型参数估计工作。由于文章篇幅限制,这里只给出在整个时期内十大城市一、二手房价格泡沫相依结构中第一棵树结构及其相依性估计结果 (见图1),而不再给出具体的RVM矩阵、估计参数矩阵、第二棵树到最后一棵树的相依结构。①对其他估计结果 (RVM矩阵、估计参数矩阵和每棵树的相依结构等)感兴趣的读者,可向作者索取。由图1可知,本研究最终从31个备选模型中(附表1)选择了代号为C、SC、F、SBB8的模型,对应的具体模型全称分别为:Clayton Copula模型、Survival Clayton Copula模型 (这个模型函数是由Clayton Copula模型函数旋转 180度后形成的)、Frank Copula模型、Survival Joe-Frank模型 (这个模型函数是由Joe-Frank Copula模型函数旋转180度后形成的)。这里不再介绍各个模型的具体公式,只重点介绍它们在相依性分析中的特点:Clayton Copula模型适合刻画具有“上尾小下尾大”的非对称相依结构特征,且要求相依性为正。Survival Clayton Copula模型适合刻画具有“下尾小上尾大”的非对称相依结构特征,且要求相依性为正。Frank Copula模型适合刻画具有“上下尾对称”特征的相依结构,且要求相依性不等于0,由此可见,该模型可同时刻画正负相依性。Survival Joe-Frank模型适合刻画具有“非对称上下尾”相依结构特征的正相关性。显然,这四种模型基本上能刻画上下尾对称或非对称的各种情况。

从图1中的子图 (a)来看,在整个研究时期内,国内十大城市一手住宅价格泡沫的相依结构出现如下显著特征:第一,城市层级聚集特征。四个一线城市①(北、上、广、深)以北京为中心聚集成一个独立区域；五个二线城市 (重庆、杭州、南京、武汉、成都)以杭州为中心聚集成一个独立区域。天津作为二线城市,并没有加入二线城市聚集区域,反而与上海相连,加入了一线城市的聚集区域。第二,地理区域聚集特征,也即城市之间地理位置越邻近,其房价泡沫之间更容易形成联系,且相依性均较强。从子图 (a)可看出,从地理位置上广州毗邻深圳,杭州与南京和武汉靠近,成都和重庆靠近,这些相邻或靠近的城市之间在一手房价泡沫相依结构中也存在直接的相依性。第三,存在处于枢纽中心地位的城市房价泡沫。北京起到了枢纽中心的地位,分别与上海、广州、武汉存在直接的联动性,各自的相依性分别为0.53(F)、0.59(SBB8)、0.52(F)。由此说明,北京一手房价格泡沫分别与上海、武汉的一手房价格泡沫之间的相依性具有对称的上下尾相依结构特征,说明北京一手房泡沫的变化与上海和武汉的一手房泡沫的变化存在显著的同步性。而北京与广州一手房价格泡沫之间存在非对称的上下尾相依结构,说明北京一手房泡沫与广州一手房泡沫在收缩时会显示出较高的同步性。与此同时,广州一手房价格泡沫与深圳一手房价格泡沫之间也存在较高的相依性,其相依性水平达到0.57且适合用SBB8 Copula模型来刻画,突显出两者之间存在非对称的上下尾相依结构特征,说明这两个城市一手房泡沫在膨胀和收缩阶段的相依性并不一致,表明各自的泡沫调整速度并不一致。同样,上海一手房价格泡沫与天津一手房价格泡沫之间存在非对称的上下尾相依性 (0.57,SBB8),说明上海一手房与天津一手房在泡沫膨胀与收缩阶段并不完全同步。杭州成了3个重点二线城市房价泡沫的枢纽中心,分别与重庆、南京和武汉之间存在直接的联动性,其相依性分别为0.55(SBB8)、0.57(SBB8)、0.45(C)。从适用的Copula模型来看,杭州与重庆和南京之间在一手房价格泡沫上存在非对称的上下尾相依结构,说明杭州一手房泡沫在膨胀阶段或收缩阶段与重庆和南京的一手房泡沫的相依性存在明显差异。与此同时,杭州与武汉在一手房价格泡沫上存在下尾相依结构,说明杭州一手房泡沫只在收缩阶段才与武汉一手房泡沫存在相依性。武汉成了连接一、二线城市房价泡沫聚集区域的重要桥梁。

从子图 (b)来看,在整个研究时期内,国内十大城市二手住宅价格泡沫的相依结构并没有像一手房价格泡沫那样出现明显的区域聚集和城市层级聚集的特征；北京和杭州也没有起到枢纽中心的作用；整个相依结构呈现为链式分布特征,只有武汉起到了一定程度上的枢纽中心的地位,分别与天津、深圳、广州直接相连,其相依性分别为0.74(SC)、0.58(F)、0.53(F),这说明武汉二手房价格泡沫与天津二手房价格泡沫之间存在上尾相依结构,而与深圳和广州的二手房价泡沫之间均存在对称的上下尾相依结构。与此同时,广州与成都 (0.57,SBB8)、成都与重庆(0.59,SC)、重庆与杭州 (0.4,SBB8)、天津与南京 (0.64,SBB8)、南京与北京 (0.47,F)、北京与上海 (0.59,SBB8)之间同样存在较高的相依性,但相依结构特征不尽相同。

图1 十大城市一、二手住宅价格泡沫相依结构 (第一棵树)

(五)十大城市房价泡沫传导机制特征

图1 虽然揭示出我国十大城市在一、二手房价格泡沫上形成的复杂相依性结构,但依然无法揭示相关联城市在房价泡沫上的因果关系。对此,为了揭示出十大城市房价泡沫相互之间的传导机制,这里采用Granger因果关系分析法来分析图1中存在相依性的各城市房价泡沫之间的因果关系,主要的分析思路是:以存在相依性的两个城市为研究对象,构建二元向量自回归 (VAR)模型,然后基于SC和HQ值最小原则确定最佳滞后阶数,再进行格兰杰因果关系检验。由于论文篇幅限制,这里不再给出各城市之间的具体检验过程,同时为了更直观看到各城市房价泡沫之间的因果关系,这里直接将最终检验结果以箭头的方式标识在房价泡沫的相依结构图上 (见图2)。图2中的箭头指向的一端为格兰杰因果关系中的果,箭头出发的一端为因,箭头上面的数值为置信度,表示这种因果关系在该置信水平上显著；双向箭头表示两者互为格兰杰因果关系。

从图2中的子图 (a)可看出,在1%的置信水平上深圳是广州的单向格兰杰原因；在10%的置信水平上,广州是北京的单向格兰杰原因；在1%的置信水平上,北京是上海的单向格兰杰原因；在5%置信水平上北京与武汉互为格兰杰原因；在1%的置信水平上,上海和天津互为格兰杰因果关系；在5%置信水平上,武汉和南京均是杭州的单向格兰杰原因；同样,在5%的置信水平上,杭州和成都均是重庆的单向格兰杰原因。从房价泡沫传导的外部来源看,深圳、天津、南京和成都成了一手房价格泡沫的外部传导源,而北京和杭州则在这个房价泡沫传导网络中扮演着枢纽中心的地位,起到承接和传递房价泡沫的作用,显示出较强的辐射力。

图2 国内十大城市一、二手住宅价格泡沫之间的因果关系

从图2中的子图 (b)可看出,十大城市二手房价格泡沫传导路径与一手房价格泡沫的传导路径差异较大。上海、深圳和杭州成为二手房价格泡沫的外部传导源。在1%的置信水平上,上海是北京的单向格兰杰原因；同样,在1%的置信水平上,北京和天津是南京的单向格兰杰原因；而武汉在1%的置信水平上是天津的单向格兰杰原因；深圳和广州在5%的置信水平上均是武汉的单向格兰杰原因；而成都在5%的置信水平上是广州的单向格兰杰原因；重庆和成都在5%的置信水平上互为格兰杰原因；杭州在5%的置信水平上是重庆的单向格兰杰原因。总的来看,国内十大城市的一、二手住宅价格泡沫的传导机制各异,各关联城市之间在房价泡沫传导机制上存在明显不对称特征。

五、结论与建议

本文采用单位根右侧ADF泡沫检验方法(BSADF)来动态测度中国十大城市的一、二手住宅价格泡沫及其存续周期时点,在此基础上采用RVine Copula方法来分析各城市房价泡沫之间的复杂相依性,最后采用格兰杰因果关系检验法来揭示各城市房价泡沫的传导机制特征。最终结论如下:

第一,国内十大城市的一、二手住宅市场均存在多个周期性价格泡沫,且市场结构性失衡严重。相比二线城市,一线城市的一手住宅市场在价格泡沫程度、泡沫次数和泡沫持续时间等方面更为严重；国内十大城市中的北京、上海、深圳、杭州、南京、成都的一手房价格泡沫要比其二手房价格泡沫严重；而广州、天津、重庆、武汉的一手房价价格泡沫要小于其二手房价格泡沫。总体上,北京的一手住宅价格泡沫最为严重,其泡沫持续至今长达10年以上仍未破灭；从各城市最严重房价泡沫存续周期来看,一线城市的房价泡沫已向部分重点二线城市蔓延。

第二,国内十大城市一手房价格泡沫的相依结构存在明显的区域聚集和城市层级聚集特征。其中,一线城市的一手住宅价格泡沫和二线城市一手住宅价格泡沫各自聚集然后相连；北京是一线城市的枢纽中心,而杭州是二线城市的枢纽中心；武汉在连接一、二线城市区域上起到了重要的桥梁作用。与此同时,城市之间在地理位置上越接近,则这两个城市在一手房价泡沫上更可能存在较高的相依性,存在房价泡沫溢出效应 (比如:广州与深圳、杭州与南京、杭州和武汉、成都与重庆),但在二手住宅价格泡沫相依结构中则不存在明显的区域聚集特征。无论是一手房市场还是二手房市场,各城市房价泡沫之间的相依性普遍具有非对称的上下尾相依结构特征。

第三,十大城市之间存在非对称的房价泡沫传导机制。在一手住宅市场中,深圳、天津、南京和成都是房价泡沫的外部传导源,扮演着领头羊的地位；北京和杭州则发挥“蓄水池”般的吸收和扩散的作用。在二手住宅市场中,上海、深圳和杭州是房价泡沫的外部传导源,扮演着领头羊的地位,而武汉则同样起到了承上启下的枢纽中心作用。总体上,无论是一手住宅市场还是二手住宅市场,各关联城市在房价泡沫相互作用机制上普遍存在非对称的格兰杰因果关系,说明存在非对称的房价泡沫传导机制。

根据上述研究结论,提出如下抑制房价泡沫及防范房价泡沫传染风险的建议:

第一,实施差异化和分层次的房价泡沫防范措施。我们需要意识到高房价并不意味着高泡沫,因此,房地产调控的重点应该放在抑制房价泡沫过度膨胀及防止泡沫破灭风险方面,而非仅关注房价的高低。对此,一方面,监管层需要采用合适的方法来实时监测国内一线城市和部分重点二线城市房价泡沫程度及其演化进程,同时做好房价泡沫预警工作,针对刚出现泡沫的城市采取有力措施并予以抑制；另一方面,要根据各城市一、二手住宅市场泡沫程度及其存续周期差异,采取差异化和分层次的房价泡沫抑制策略,避免采取“一刀切”的做法,对泡沫严重的城市优先调控,对无泡沫城市则保持观望。

第二,基于各城市房价泡沫存在的区域聚集特征来建立抑制房价泡沫的区域性协同机制。当前,国内各城市政府均是独立对管辖范围内的房地产市场进行监管,在制定具体的调控措施时往往没有考虑到该城市房价泡沫与其他相邻城市房价泡沫之间存在溢出效应和区域聚集特征,这些特征无疑将会大幅削弱各地政府的调控效果,因此有必要超越单个城市层面,结合各城市房价泡沫之间的相依结构特征和区域聚集特征来建立区域性的抑制房价泡沫协同机制。这主要表现在城市房价泡沫预警、房价泡沫抑制措施及实施时机等方面,各城市需要就信息进行共享并相互合作,避免各城市监管措施的冲突,从而提升区域性防控措施的协同效应。

第三,重点抑制扮演领头羊角色的城市房价泡沫并阻断其泡沫传导路径。在国内十大城市一手住宅市场中,深圳、天津、南京和成都起到了房价泡沫领头羊的作用；在二手房市场中,上海、深圳和杭州同样起到了领头羊的作用,因此,有必要采取有力措施抑制这些城市的泡沫程度,降低其对其他城市的“示范”效应。与此同时,北京和杭州、武汉分别在一、二手房泡沫传导路径中起着关键的中介作用,对此,需要采取措施降低这些城市与关联城市之间的联动性,从而在一定程度上抑制甚至阻断房价泡沫沿着相依结构路径向外扩散。

附 录

表A1 备选的Copula类型及其代号

［1］Phillips P C B,Wu Y,Yu J.Explosive Behavior in the 1990s NASDAQ:When Did Exuberance Escalate Asset Values? ［J］.International Economic Review,2011,52(1):201－226.

［2］Phillips P C B,Yu J.Dating the Timeline of Financial Bubbles During the Subprime Crisis［J］.Quantitative Economics,2011(2):1759－7331.

［3］Chen X,Funke M.Real-time Warning Signs of Emerging and Collapsing Chinese House Price Bubbles［J］.National Institute Economic Review,2013(223):39－48.

［4］Yiu M S,Yu J,Jin L.Detecting Bubbles in Hong Kong Residential Property Market［J］.Journal of Asian Economics,2013(28):115 －124.

［5］Kivedal B K.Testing for Rational Bubbles in the US Housing Market［J］.Journal of Macroeconomics,2013,38(4):369 －381.

［6］Phillips P C B,Shi S,Yu J.Testing for Multiple Bubbles I:Historical Episodes of Exuberance and Collapse in the SP500 ［J］.International Economic Review,2015,56(4):1043－1078.

［7］Phillips P C B,Shi S,Yu J.Testing For Multiple Bubbles:Limit Theory Of Real-time Detectors［J］.International Economic Review,2015,56(4):1079－1134.

［8］Engsted T,Hviid S J,Pedersen T Q.Explosive Bubbles in House Prices?Evidence from the OECD countries［J］.Journal of International Financial Markets,Institutions and Money,2016,40(1):14－25.

［9］Engsted T,Nielsen B.Testing for Rational Bubbles in A Coexplosive Vector Autoregression ［J］.Econometrics Journal,2012,15(2):226 －254.

［10］Zhou W X,Sornette D.Is There a Real-estate Bubble in the US? ［J］.Physica A,2006,361(1):297 －308.

［11］Zhou W,Sornette D.Analysis of the Real Estate Market in Las Vegas:Bubble,Seasonal Patterns and Prediction of the CSW Indices［J］.Physica A,2008,387(1):243－260.

［12］Chang K,Chen N,Leung C.The Dynamics of Housing Returns in Singapore:How Important Are the International Transmission Mechanisms? ［J］.Regional Science and Urban Economics,2012,42(3):516－530.

［13］Caspi I.Testing for A Housing Bubble at the National and Regional Level:The Case of Israel［J］.Empirical Economics,2015(8):1 －34.

［14］李维哲,曲波.地产泡沫预警指标体系与方法研究［J］.山西财经大学学报,2002(2):99－101.

［15］吕江林.我国城市住房市场泡沫水平的度量［J］.经济研究,2010(6):28－41.

［16］周京奎,曹振良.中国房地产泡沫与非泡沫——以投机理论为基础的实证分析［J］.山西财经大学学报,2004,26(1):53－57.

［17］姜春海.中国房地产市场投机泡沫实证分析［J］.管理世界,2005(12):71－84.

［18］苑德宇,宋小宁.中国区域房价泡沫测度及空间传染性研究——基于2001—2005年35个大中城市面板数据的实证分析［J］.上海财经大学学报,2008,10(3):78－85.

［19］吕炜,刘晨晖.财政支出、土地财政与房地产投机泡沫［J］.财贸经济,2012(12):21－30.

［20］范新英,张所地,冯江茹.房地产价格泡沫测度及区域差异性研究［J］.经济研究,2013(11):48－53.

［21］韩德宗.基于West模型的房地产泡沫的实证研究［J］.当代经济科学,2005,27(5):6－11.

［22］王春雷.住宅市场价格泡沫及预警机制研究［D］.武汉:华中科技大学,博士学位论文,2008.

［23］Van Norden S,Vigfusson R.Avoiding the Pitfalls:Can Regime-switching Tests Reliably Detect Bubbles? ［J］.Studies in Nonlinear Dynamics and Econometrics,1998,3(1):1－22.

［24］史兴杰,周勇.房地产泡沫检验的Switching AR模型［J］.系统工程理论与实践,2014(3):676－682.

［25］Bedford T,Cooke R M.Probability Density Decomposition for Conditionally Dependent Random Variables Modeled by Vines ［J］.Annals of Mathematics and Artificial Intelligence,2001,32:245－268.

［26］Dißmanna J,Brechmanna E C,Czadoa C,Kurowicka D.Selecting and Estimating Regular Vine Copula and Application to Financial Returns［J］.Computational Statistics&Data Analysis,2013,59(3):52－69.

［27］郭文伟.全球股市泡沫测度及其相依结构分析［J］.广东财经大学学报,2016(4):61－71.