指数熔断机制加剧了市场波动吗?——基于中国A股市场的自然实验

李梦雨 魏熙晔

一、引言及文献综述

中国证券市场在2015—2016年经历了剧烈的异常波动,多个交易日出现千股跌停、千股停牌的异象。为防范系统性风险,维护市场稳定,中国证监会于2016年1月1日在A股市场上引入指数熔断机制,却在实行一周内两次触发7%的阈值并提前收市①指数熔断机制于2016年1月4日和1月7日两次被触发,分别导致4.24万亿元和3.8万亿元的市值蒸发。,最终于1月8日宣告暂停。熔断机制是否为市场大跌的罪魁祸首,是否加剧了市场波动,是否存在“磁吸效应”②磁吸效应是指实行涨跌停或熔断等机制后,证券价格将要触发强制措施时,同方向的投资者害怕流动性丧失而抢先交易,反方向的投资者为等待更好的价格而延后交易,造成证券价格加速达到该价格水平的现象。(magnet effect)?上述问题受到学者与政策制定者的高度关注。事实上,自1987年10月19日的“黑色星期一”后,学术界就开始了熔断机制方面的理论与实证研究,而2010年5月6日的“闪崩”事件更是引发了国内外学者对熔断机制利弊的热烈讨论。目前,世界范围内许多交易所都设定了指数或个股熔断机制③指数熔断机制是指当某一特定指数的波动幅度触及证券交易所规定的阈值时,整个市场的所有股票均停止交易一段时间；个股熔断机制是指单只股票的价格波动幅度触及证券交易所规定的阈值时,该股票停止交易一段时间。,然而学者们在熔断机制对市场质量产生的影响方面却始终各持己见。

按照Fama(1970)［1］的有效市场假说,在半强势有效市场中资产价格可以反映所有公开信息,因此熔断机制会因人为干预市场价格调整使得其偏离最优结果,故而会具有以下负面效应:(1)阻碍互惠交易(Grossman,1990［2］)；(2) 延缓价格发现(Fama,1989［3］)；(3) 产生磁吸效应 (Subrahmanyam,1994［4］)；(4) 导致波动性溢出(Lehmann,1989［5］)；(5) 增加交易成本 (Subrahmanyam,1997［6］)。相关的实证研究也较为丰富, 包括 Kuhn 等(1991)［7］、 Ferrris等(1992)［8］、Santoni 和 Liu(1993)［9］、Lee 等(1994)［10］、 Ackert等 (2001,2005)［11－12］、 Goldstein和 Kavajecz(2004)［13］等。

然而当证券市场偏离完全信息和完全竞争市场时,熔断机制在理论上可以提高市场质量和投资者福利。其中较为成熟的观点包括:(1)减少信息不对称 (Spiegel和 Subrahmanyam,2000［14］)；(2) 降低交易风险 (Greenwald 和 Stein,1991［15］；Kodres 和O'Brien,1994［16］)；(3) 在衍生品市场中降低杠杆投资者的交易对手风险 (Brennan,1986［17］；Chowdhry和Nanda,1998［18］)；(4) 通过减少噪声交易者的交易来降低证券价格偏离基本面价值的概率,从而平抑市场过度波动 (Westerhoff,2003［19］)。但是在实证研究中,支持上述理论的文献并不多见,唯有Lauterbach和 Ben-Zion(1993)［20］、 Bildik 和 Gülay(2006)［21］的研究验证了当市场价格大幅偏离真实价值时,熔断机制会给予市场充分的冷却和反应时间,并化解因投资者撤离市场而导致的订单不平衡现象,从而降低波动率、提高流动性。

近年来,随着程序化交易和“乌龙指”(fat finger)现象的出现,对熔断机制的讨论亦呈雨后春笋之势,研究方法和角度也更为新颖。Gomber等(2012)［22］、Subrahmanyam(2013)［23］、Nicholas(2016)［24］、 Bruger 和 Linton.(2014)［25］、 Goldstein(2015)［26］分别从单个市场和卫星市场、程序交易与联合熔断、原油期货市场、单只股票熔断、交易上下限与波动性传导机制等方面考察了熔断机制与市场质量的关系。其中Bruger和Linton(2014)［25］的研究发现,从个股层面来看,熔断机制在股票收益为负时对交易量、交易频数以及利润方差变化均产生了负面效应,但在收益为正时却无显著影响；从市场层面来看,当股市整体下跌时,熔断机制使得噪声交易减少、定价效率提高,因此有利于市场的稳定。

上述理论研究大多基于做市商制度,实证文献也主要关注发达市场,而我国属于新兴市场国家,具有散户交易者居多、羊群效应显著等特征,在股市下跌时容易引发“踩踏效应”,使得熔断机制的实施效果有所不同。因此与已有文献相比,本文具有两个方面的边际贡献:其一,基于指数熔断机制出台与暂停的自然实验,使用倾向评分匹配法与双重差分法分析其对市场波动性的影响,说明该制度并非大盘下挫的主因,补充了市场异常波动期间熔断机制的效应研究；其二,深入探究订单驱动市场中指数熔断机制产生“磁吸效应”的原因及表现,证实该制度在已实施“涨跌停板”的新兴市场国家容易造成流动性恐慌,丰富了熔断机制领域的研究成果。

本文的后续安排如下:第二部分提出研究假设,第三部分为模型构建与数据说明,第四部分分析实证结果,第五部分进行稳健性检验,最后是主要结论与政策建议。

二、研究假设

H1:证券市场下跌期间指数熔断机制并未增加市场波动性。

不可否认的是,在指数熔断机制实施期间,沪深300指数从下跌5%到7%的时间明显缩短,其间的波动率也显著增大,这很可能意味着指数熔断机制在我国存在较强的磁吸效应②磁吸效应通常具有以下三个特点:一是在接近熔断阈值时,价格上涨或下跌的速度会越来越快；二是熔断机制实施后指数触发熔断的概率会明显高于其在熔断价格水平附近但不触发的概率；三是磁吸效应发生过程中往往伴随着价格的剧烈波动和成交量的显著变化。。根据 Subrahmanyam(1994)［4］,磁吸效应的作用机理为:当证券价格将要触发熔断机制时,无法保持耐心的投资者会因害怕流动性丧失而抢先交易,而潜在的对手方则倾向于等待更好的价格而延后交易。此外,指数越是接近熔断阈值,相反头寸持有者的心理压力就越大,从而迫使他们进行对冲,使得市场价格更加趋向熔断价格 (Fama,1989［3］)。鉴于此, 我们提出假设2。H2:指数熔断机制在我国存在明显的磁吸效应。

三、模型构建与数据说明

(一)模型构建

鉴于影响市场波动性的因素包括股票价格、成交量、成交金额等诸多方面,简单比较指数熔断机制实施前后沪深300指数波动率的变化显然有失偏颇。此外,股指的上涨与下跌,投资者情绪的高涨与低迷,都会造成市场波动性随之改变。因此,为克服内生性问题,避免选择性偏差,本文采用研究“处理效应”的通常做法,通过构建倾向评分匹配模型和双重差分模型,来分析指数熔断机制的出台与暂停对市场波动性的影响。

1.指数熔断机制与市场波动率的模型构建。

本文首先研究指数熔断机制与市场波动率之间的关系。为此,我们需要构建度量市场波动率的指标。考虑到股票价格指数序列具有波动集群 (volatility clustering)和尖峰厚尾 (leptokurtosis和fat-tail)等特征,本文运用AR(2)－GARCH(1,1)模型对沪深300指数的涨跌幅Chg、对数成交量Trv和对数成交额Amt进行估计,计算出沪深300指数的价格波动率Vol、成交量波动率Vtrv和成交额波动率Vamt,具体公式如下:

其中:yt代表 Chgt、 Trvt和 Amtt；vt～IDD(0,1),vt与yt,vt与ut均相互独立；E(ht)＝E(u2t)＝而即为度量市场波动率的指标Volt、Vtrvt和Vamtt。

在此基础上,本文使用倾向评分匹配法来考察指数熔断机制是否增加了市场波动率。为阐述上述方法的基本原理,我们以沪深300指数的价格波动率Vol为例,对于稳健性检验中其他变量的估计可如法炮制,不再赘述。为此,我们引入一个二元虚拟变量Treati。当数据来自处理组,即指数熔断机制被触发的交易日时,Treati＝1；当数据来自对照组,即指其他交易日时,Treati＝0。令Volit为第i个交易日时刻t的沪深300指数价格波动率,Vol1it为处理组的Volit,Vol0it为对照组的Volit。考虑该波动率在指数熔断机制实施期间的平均处理效果ATT1(average effect of treatment on the treated)

据对《嘉泰会稽志》引用《旧经》情况的分析,作为地名的“会稽”向山系名称转化的情况,是在两宋时期才发生的。

估计式 (2)的困难之处在于,｜Treati＝1)事实上并不可测,而倾向评分匹配法有效地解决了这类“反事实” 问题 (Heckman等,1998［33］)。具体而言,我们首先根据沪深300指数的涨跌幅Chg、对数成交量Trv、对数成交额Amt等控制变量,通过Probit模型计算出每一个观测值成为处理组的概率,作为倾向得分；然后依据倾向得分为每一个处理组样本寻找匹配样本；最后计算匹配后处理组与对照组的差距,从而模拟出“反事实”情形下的平均处理效果。

值得注意的是,倾向评分匹配法的有效性依赖于两个条件:(1)条件独立假设 (conditional independence assumption),即经过倾向评分匹配后不可观测的因素不影响试验；(2)共同支撑假设 (common support assumption),即处理组和对照组样本的倾向得分有足够多的重叠区域。前者保证了匹配过程不存在“选择性偏差”,而后者保证了处理组样本能够找到与其配对的对照组样本。满足上述两个条件的平均处理效果ATT1的估计方程为

其中:I1与I0分别为处理组与对照组集合；S为共同支撑域,即在该集合内处理组样本的倾向得分不高于 (低于)对照组样本的倾向得分的最大 (小)值；n1为I1∩S中的样本个数；w(i,j)为匹配后对照组样本的权重。

2.指数熔断机制与磁吸效应的模型构建。

在分析了指数熔断机制与市场波动率之间的关系之后,我们需要研究指数熔断机制是否存在磁吸效应。鉴于此,本文运用基于倾向评分匹配的双重差分法来考察沪深300指数在即将触发熔断阈值时是否出现了异常波动。为此我们需要在上文的基础上再构造一个二元虚拟变量Timet。当沪深300指数的累计涨跌幅接近熔断阈值,即累计涨跌幅的绝对值达到4%及以上时,Timet＝1；其他时间Timet＝0。根据前文所述的原理,本文采用最临近匹配法 (nearest neighbor matching)为处理组样本选择了匹配样本。匹配后沪深300指数价格波动率的变化量的平均处理效果为ATT2。

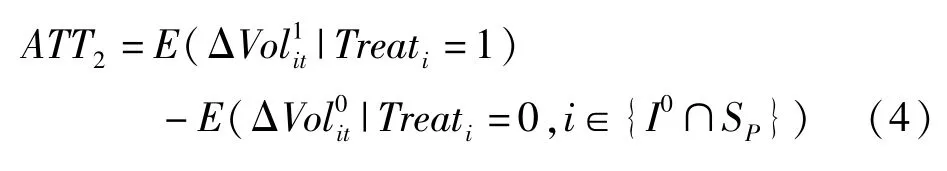
更进一步,式 (4)的一个等价性的可以用于实证检验的表述为①限于篇幅,文中没有给出相应的证明过程,感兴趣的读者可以向作者索取。

其中:X为控制变量集合,包括沪深300指数的涨跌幅Chg、对数成交量Trv和对数成交额Amt；εit为随机误差项。交叉项Treati×Timet的估计系数刻画了沪深300指数在熔断阈值附近的价格波动率情况。若显著大于0,则意味着指数熔断机制确实存在磁吸效应；反之,则磁吸效应并不明显。

(二)数据说明

本文的数据来源为Wind数据库中的1分钟序列。由于实行指数熔断机制的初衷为抑制2015年下半年开始的证券市场异常波动,且两档熔断阈值分别为5%和7%,因此我们首先将时间跨度限制为2015年6月1日至2016年6月1日,然后选取沪深300指数价格涨跌幅较大的17个交易日作为样本。②样本交易日按照沪深300指数跌幅由大到小排列分别是:2015－08－24、2015－07－27、2015－06－26、2016－01－07、2015－08－25、2016－01－04、2015－07－08、2015－08－18、 2016－02－25、 2016－01－26、 2015－06－19、 2015－07－03、 2015－11－27、 2016－01－11、 2015－07－01、 2015－08－21、 2015－06－18。其中,处理组为2016年1月4日与1月7日两个交易日的数据；而对照组为其他15个交易日的数据。此外,我们还根据通常文献的做法,对主要变量的缺失值和异常值进行了处理与剔除。

四、实证结果分析

(一)统计性描述

表1为除虚拟变量外其他变量的统计特征,在剔除了经AR(2)－GARCH(1,1)模型处理的缺失值后,共得到3 741个有效样本①所有变量的频率均为1分钟。。其中,沪深300指数1分钟涨跌幅Chg的均值为负,反映出样本交易日确实取自证券市场下跌期间；所有变量的最小值最大值都相去甚远,除价格波动率Vol外,其他变量的标准差较大,可见沪深300指数大幅下挫期间的市场波动较为强烈。

表1 变量统计特征

(二)指数熔断机制对市场波动率的影响

在运用倾向评分匹配法检验指数熔断机制实施期间市场波动率是否显著增大之前,我们首先对条件独立假设进行了检验。进行此检验的方法较多,包括DW规范检验 (DW specification test)、标准偏差检验(standardised differences test)以及霍特林检验 (Hotelling test)等。但对于同一组数据使用不同检验方法,其结果可能大相径庭 (Lee,2005［34］)。本文采用目前使用较广的Smith和Todd(2005)［35］的标准偏差方法进行平衡性检验,计算出匹配后处理组与对照组基于控制变量Xk②Xk为沪深300指数的涨跌幅Chg、对数成交量Trv及对数成交额Amt。的标准偏差SDIFF(Xk),其公式如下:

上述标准偏差越小,说明匹配效果越好。对于其判断标准,Rosenbaum 和 Rubin(1983)［36］指出, 当20时可认为匹配效果不好。本文的检验结果通过了匹配平衡检验,说明处理组与对照组在匹配变量上不存在显著差异。

在此基础上,我们利用最临近匹配 (nearest neighbor matching)、半径匹配 (radius matching)、核匹配 (kernel matching)以及分层匹配 (stratification matching)四种方法,检验了与其他跌幅较大的交易日相比,指数熔断机制被触发的两个交易日沪深300指数的价格波动率是否显著增大。表2显示了匹配后的平均处理效果,在估计中我们设置了共同支撑假设,并通过自举法 (bootstrap)100次获得回归系数的t值。

表2 沪深300指数价格波动率的平均处理效果

由表2可知,四种匹配方法下处理组的价格波动率比对照组约大0.005,但上述估计结果均不显著。这说明无论是采用一对一的最临近匹配还是使用满足条件的所有对照组样本的半径匹配、核匹配和分层匹配,2016年1月4日和1月7日沪深300指数的价格波动率较样本期间内其他具有较大跌幅的交易日并没有显著差别。故而指数熔断机制的实施并没有加大股市大幅下挫期间的市场波动率,假设1得以验证。

(三)指数熔断机制的磁吸效应研究

指数熔断机制最饱受诟病的负面作用就是磁吸效应,而5%与7%两档熔断阈值如此接近,更是容易引发同方向投资者因害怕流动性丧失而抢先交易,反方向投资者为等待更好价格而延后交易。表3展示了沪深300指数日跌幅超过5%的交易日在熔断阈值附近的下跌时间。从中可以看出,日跌幅超过5%的交易日共14个,指数由下跌4%到5%的平均时间为12分钟③12分钟的计算方法为所有14个交易日－5%～－4%这一列数的算术平均值；后文28分钟的计算方法与之类似。；日跌幅超过7%的交易日有6个,指数由下跌5%到7%的平均时间为28分钟。关注2016年1月4日与1月7日的相关数据,其中1月4日在5%熔断阈值附近的表现基本正常,但在触发第一档阈值后,仅过了9分钟便再次触发第二档阈值；而1月7日指数由下跌4%到5%仅用了2分钟,第一档阈值被触及后不到3分钟的时间就导致大盘收市。因此从数据直觉的意义上,指数熔断机制确实存在磁吸效应,且在第一档阈值被触发后变得更加明显。

表3 沪深300指数在熔断阈值附近的下跌时间

为进一步检验指数熔断机制的磁吸效应,我们运用基于倾向评分匹配的双重差分法,考察了当沪深300指数的涨跌幅到达4%后,其价格波动率是否出现异常。①由于处理组样本个数有限 (即Treat＝1且Time＝1的样本共12个),因此我们并未能验证由－7% ～－5%这段时间Vol的异常表现。表4展示了变量Vol平均处理效果的回归结果。其中回归式 (1)为未添加任何控制变量的估计结果；回归式 (2)和 (3)分别为添加控制变量后使用面板个体固定效应和时间固定效应的估计结果。

表4 Vol平均处理效果的回归结果

由表4可知,三个回归方程中的交叉项估计系数均为正,且具有1%的显著性水平。这说明指数熔断机制实施期间,沪深300指数的价格波动率在超过4%后确实出现异常,平均而言较未实行时高出约0.04,体现出该制度推出后交易者因流动性恐慌而纷纷抛售手中股票,从而导致价格下跌速度加快,假设2得到验证。此外,控制变量的回归系数也符合预期,即涨跌幅、成交量与成交额均与价格波动率呈正相关关系,且上述结果在1%的水平下显著。

五、稳健性检验

为验证上述结果的稳健性,本文首先将全样本进行了分段回归,其中子样本1为指数熔断机制推出前与两次触发熔断的交易日,子样本2为指数熔断机制暂停后与两次触发熔断的交易日。运用子样本的估计结果与前文结论一致,限于篇幅,本文未报告具体的实证结果。

其次,本文选取沪深300指数的成交量波动率和成交额波动率,运用相同的计量方法,检验了指数熔断机制是否增加了市场波动这一假设,回归结果如表5所示。从中可以看出,除最临近匹配法下的成交额波动率具有10%的显著性外,其他回归系数均不显著,证明总体而言指数熔断机制并未对市场波动性产生较大影响。

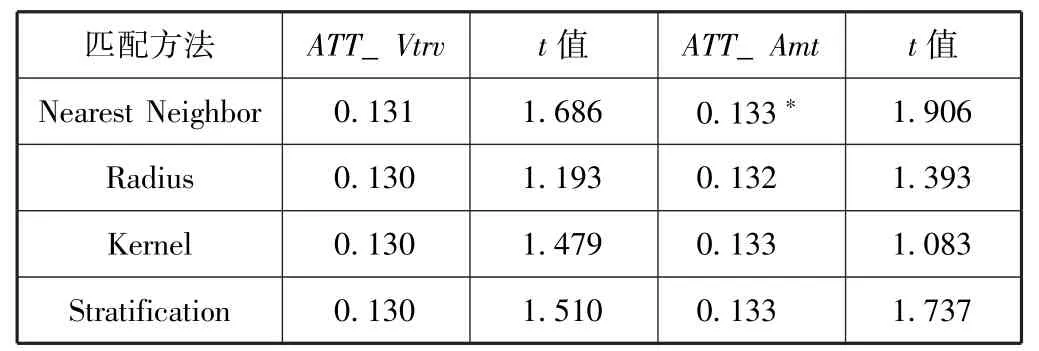
表5 沪深300指数成交量和成交额波动率的平均处理效果

鉴于磁吸效应的表现之一为成交量和成交额的剧烈变化,因此在稳健性检验中我们再次运用基于倾向评分匹配的双重差分法考察了沪深300指数成交量和成交额波动率在累计跌幅超过4%后的表现,回归结果如表6所示。其中回归式 (4)～(6)的因变量为Vtrv；回归式 (7)～(9)的因变量为Vamt。

表6 Vtrv与Vamt平均处理效果的回归结果

由表6可知,所有交叉项的估计系数均为正,且在1%的水平下显著。可见在指数熔断机制实施期间,当沪深300指数的累计跌幅接近熔断阈值时,成交量波动率和成交额波动率均呈现明显上升态势,磁吸效应的存在性也就不言而喻了。

六、主要结论与政策建议

本文通过倾向评分匹配法与双重差分法,考察了证券市场暴跌情形下指数熔断机制的实施效果,结果发现:一是指数熔断机制实行期间沪深300指数的波动率没有显著增加,说明该制度并非市场波动加大的原因；二是当沪深300指数的累计跌幅接近熔断阈值时,指数下跌速度加快,价格、成交量和成交额的波动率都显著增加,证明磁吸效应确实存在。

针对上述发现,本文认为,虽然指数熔断机制在纽约证券交易所、纳斯达克证券交易所、多伦多证券交易所、韩国证券交易所、印度国家证券交易所等诸多市场上得以应用 (Brugler和Linton,2014［25］), 但中国股票市场的波动水平整体较高,非理性投资者所占比重也较大,因此在熔断机制的设计上存在一些问题。首先,第一档熔断阈值较低,大大提高了触发指数熔断的可能性；其次,第二档熔断阈值也较低,使得触发全天交易暂停的概率增加；再次,第一、二档熔断阈值的间隔较小,导致磁吸效应在我国异常明显；最后,熔断时长占日交易总时间的比例较高,容易引发流动性短缺与恐慌性抛售。

指数熔断机制在我国仅实施4个交易日就告暂停,的确值得监管层深度反思。目前A股市场已存在涨跌停板制度,短时间内应不会重启指数熔断机制。今后证券监管部门在出台新的交易机制时,应结合我国资本市场的实际情况,进行充分的理论论证和深入的量化分析,避免高昂的制度试错成本,从而实现维护证券市场稳定和保护投资者权益的目的。

［1］Fama E F.Efficient Capital Markets:A Review of Theory and Empirical Work［J］.The Journal of Finance,1970,25(2):383－417.

［2］Grossman S J.Introduction to NBER Symposium on the October 1987 Crash ［J］.Review of Financial Studies,1990,3(1):1 －3.

［3］Fama E F.Perspective on October 1987,or What Did We Learn form the Crash?［M］//Kamphuis R W,Jr Kormendi R C,Waston J.Black Monday and the Future of the Financial Markets.Irwin,Homewood,III,1989:16－45.

［4］Subrahmanyam A.Circuit Breakers and Market Volatility:A Theoretical Perspective［J］.The Journal of Finance,1994,3(1):237－254.

［5］Lehmann B N.Commentary:Volatility,Price Resolution,and the Effectiveness of Price Limits［M］//Regulatory Reform of Stock and Futures Markets.Springer Netherlands.1989:107－111.

［6］Subrahmanyam A.The Exante Effects of Trade Halting Rules on Informed Trading Strategies and Market Liquidity ［J］.Review of Financial Economics,1997,6(1):1－14.

［7］Kuhn B A,Kurserk G J,Locke P.Do Circuit Breakers Moderate Volatility?Evidence from October 1989 ［J］.Review of Futures Markets,1991,10(1):426－434.

［8］Ferris S P,Kumar R,Wolfe G A.The Effect of SEC-ordered Suspensions on Returns,Volatility,and Trading Volume ［J］.Financial Review,1992,27(1):1－34.

［9］Santoni G J,Liu T.Circuit Breakers and Stock Market Volatility［J］.Journal of Futures Markets,1993,13(3):261－277.

［10］Lee C,Ready M J,Seguin P J.Volume,Volatility,and New York Stock Exchange Trading Halts［J］.The Journal of Finance,1994,49(1):183－214.

［11］Ackert L F,Church B,Jayaraman N.An Experimental Study of Circuit Breakers:The Effects of Mandated Market Closures and Temporary Halts on Market Behavior［J］.Journal of Financial Markets,2001,4(2):185 －208.

［12］Ackert L F,Church B K,Jayaraman N.Circuit Breakers with Uncertainty about the Presence of Informed Agents:I Know What You Know…I Think ［J］.Financial Markets,Institutions and Instruments,2005,14(3):135 －168.

［13］Goldstein M A,Kavajecz K A.Trading Strategies during Circuit Breakers and Extreme Market Movements［J］.Journal of Financial Markets,2004,7(3):301－333.

［14］Spiegel M,Subrahmanyam A.Asymmetric Information and News Disclosure Rules ［J］.Journal of Financial Intermediation,2000,9(4):363－403.

［15］Greenwald B C,Stein J C.Transactional Risk,Market Crashes,and the Role of Circuit Breakers ［J］.Journal of Business,1991,2(1):443－462.

［16］Kodres L E,O'Brien D P.The Existence of Pareto-superior Price Limits［J］.The American Economic Review,1994,84(4):919－932.

［17］Brennan M J.A Theory of Price Limits in Futures Markets［J］.Journal of Financial Economics,1986,16(1):213 －233.

［18］Chowdhry B,Nanda V.Leverage and Market Stability:The Role of Margin Rules and Price Limits［J］.The Journal of Business,1998,71(2):179－210.

［19］Westerhoff F.Speculative Markets and the Effectiveness of Price Limits ［J］.Journal of Economic Dynamics and Control,2003,28(3):493－508.

［20］Lauterbach B,Ben-Zion U R I.Stock Market Crashes and the Performance of Circuit Breakers:Empirical Evidence ［J］.The Journal of Finance,1993,48(5):1909－1925.

［21］Bildik R,Gülay G.Are Price Limits Effective?Evidence from the Istanbul Stock Exchange ［J］.Journal of Financial Research,2006,29(3):383－403.

［22］Gomber P,Haferkorn M,Lutat M,Zimmermann K.The Effect of Single-stock Circuit Breakers on the Quality of Fragmented Markets［M］//Enterprise Applications and Services in the Finance Industry.Springer Berlin Heidelberg,2012:71－87.

［23］Subrahmanyam A.Algorithmic trading,the Flash Crash,and Coordinated Circuit Breakers［J］.Borsa Istanbul Review,2013,13(3):4－9.

［24］Nicholas A.The Role of Circuit Breakers in the Oil Futures Market［J］.Journal of Economics and Finance,2016,4(10):1 －16.

［25］Brugler J,Linton O B.Single Stock Circuit Breakers on the London Stock Exchange:Do They Improve Subsequent Market Quality? ［J］.SSRN Working Paper,2014.

［26］Goldstein M A.Circuit Breakers,Trading Collars,and Volatility Transmission across Markets:Evidence from NYSE Rule 80A ［R］.SSRN Working Paper,2015.

［27］De Long B,Shleifer A,Summers L,et al.Positive Feedback Investment Strategies and Destabilizing Rational Speculation ［J］.The Journal of Finance,1990,45(2):379－395.

［28］Bondt W F M,Thaler R.Does the Stock Market Overreact? ［J］.The Journal of Finance,1985,40(3):793 －805.

［29］朴树,俞乔.有限理性、动物精神及市场崩溃:过度自信、有限参与和资产价格泡沫［J］.经济研究,2006(4):115－127.

［30］Banerjee A V.A Simple Model of Herd Behavior［J］.The Quarterly Journal of Economics,1992,107(3):797 －817.

［31］Graham J R.Herding among Investment Newsletters:Theory and Evidence［J］.The Journal of Finance,1999,54(1):237 －268.

［32］崔巍.金融市场中羊群行为的模拟研究及启示［J］.北京大学学报 (哲学社会科学版),2009(6):68－74.

［33］Heckman J J,Ichimura H,Todd P.Matching As an Econometric Evaluation Estimator［J］.The Review of Economic Studies,1998,65(2):261－294.

［34］Lee G.PSM and Public Employees’ Work Performance ［J］.Korean Society and Public Administration,2005,16(1):81 －104.

［35］Smith J A,Todd P E.Does Matching Overcome LaLonde's Critique of Nonexperimental Estimators? ［J］.Journal of Econometrics,2005,125(1):305－353.

［36］Rosenbaum P R,Rubin D B.The Central Role of the Propensity Score in Observational Studies for Causal Effects ［J］.Biometrika,1983,70(1):41－55.