各种集合理论的哲学基础及其区别

梁俊奇

(商丘师范学院 数学与统计学院，河南 商丘 476000)

各种集合理论的哲学基础及其区别

梁俊奇

(商丘师范学院 数学与统计学院，河南 商丘 476000)

简单介绍普通集合、模糊集合、可拓集合和粗糙集合等集合理论的哲学基础，并指出其主要区别.

普通集合；模糊集合；可拓集合；粗糙集合；哲学基础；反演集合

0 引 言

自1871年康托尔(Cantor)提出集合(set)理论以来，集合成为数学的基本概念，集合理论成为现代数学的基础理论.但是，随着社会与科学技术的发展，人们逐渐发现了许多康托尔集合不能描述的事物.为了描述这些事物，美国学者扎德(L.A.Zadeh)于1965年提出了模糊集合(Fuzzy set)理论[1]，从而使数学摆脱了康托尔集合理论思想的束缚，促使集合理论向多样性方向发展.1982年以后，国内外学者又先后提出了可拓集合(Extension set)[2]、粗糙集合(Rough set)[3]-[4]、反演集合(Inversion set)理论[5]等.本文试图从这些集合理论的哲学基础入手，指出它们之间的主要区别，从哲学的角度把握数学基础理论，以期认识各种集合理论的统一性.

1 普通集合的哲学基础

1871年，康托尔提出了普通集合或清晰集合概念.在普通集合概念中，给定一集合A和任一元素x，要么x属于A，要么x不属于A，二者必居其一，绝不模棱两可.因此，普通集合的哲学基础是：形式逻辑的矛盾律和排中律，即：“A不能既是B又不是B”和“A是B或不是B”.所谓形式逻辑矛盾是指事物肯定性概念(是)和否定性概念(非)之间的矛盾.矛盾双方“有我无你”，“势不两立”.它坚持一个公式：“是则是，否则否，除此之外，都是鬼话.”即普通集合描述的是客观世界中“非此即彼”的现象.然而，由于在客观世界中，并非所有现象都是非此即彼现象，因此，普通集合的描述不能囊括客观世界中的所有现象.从而导致后来产生了各种各样的广义集合理论.

2 模糊集合的哲学基础

在客观世界中，确实存在着既不是百分之百是B，又不是百分之百不是B的现象，许多事情在“是”与“非”之间存在着一个中介过渡阶段.一个典型例子是“秃子悖论”：有一根头发算不算秃？有一根头发不算秃不合常理，当然应该算秃.那么两根呢？也应该算秃，有谁见过脑壳上仅有两根头发就欣喜若狂地宣称自己不是秃子的人？现在改用数学归纳法，如果n根头发算不算秃？n根头发算秃，n+1根头发不算秃不合常理，有谁辨别秃子是扒着人家脑袋数头发，“多了一根！不算秃.”但是，如果n+1根头发算秃，则一根一根的加上去，满头青发都是秃，人人都是秃子.此类例子很多.例如：年老与年轻；高个子与矮个子；美与丑；胖与瘦；有矿与无矿；多与少；大与小等等.这些例子都能说明：有些事情失去中介过渡阶段，思维会引起混乱.故普通集合的哲学基础——形式逻辑的矛盾律和排中律不能全面正确地反映客观世界.由于普通集合的描述不能囊括客观世界中的各种现象，客观世界中确实存在有既不是百分之百是B，又不是百分之百不是B的中介过渡阶段，从而启示扎德于1965年提出了模糊集合(Fuzzyset)理论.从哲学角度讲，扎德是放弃了形式逻辑的排中律，而保留了矛盾律，即在是“B”与不是“B”之间增加了一个模糊中介.也就是在前面“秃子悖论”中的“秃”与“不秃”之间增加了一个叫做“有些秃”的模糊中介(边界).在模糊集合中，论域中任一元素，或百分之百属于B，或百分之百不属于B，或以百分数的形式归属于中介过渡(模糊)区域.换言之，模糊集合的哲学基础是：形式逻辑矛盾律+模糊中介边界(排中律的替代品).

3 可拓集合的哲学基础

上述的普通集合涉及的是：“是”与“非”；模糊集合涉及的是“是”、“模糊中介边界”、“非”.1983年，我国学者蔡文教授受工人将高度超过车间大门的机器搬运进车间里事件的启示，以及受“罗素悖论”的影响，提出了可拓集合概念.蔡文教授注意到：机器由于高度超过车间大门的高度，因而不属于可以搬进车间里的物体集合.但是，变换事物的特征，把小于入门高度的长换为高，这时的机器就变为属于能搬进车间里物体的集合的元素.由此，蔡文教授建立了能够描述事物可变性的可拓集合概念.在可拓集合中，一个元素要么是属于B，要么是不属于B，要么这个元素是原本不属于B的但可以转变成为属于B(称之为可拓域)，要么这个元素是既属于B又是不属于B的一个中间状态(称之为是对应“中间”事物的临界).文[2]提出了可拓集合及其可拓域、稳定域、零界等概念，用它们来描述“是”与“非”的相互转化，从而能定量地表述事物的质变和量变的过程，而零界概念则描述了事物“既是又非”的质变点.这些为矛盾问题的解决提供了合适的数学工具.不难看出，可拓集合与普通集合相比，有两点变化，一是在“非”区域内划出一个可以在一定条件下转化为“是”区域的子区域，即是在不属于B的范围内增加了一个可以转化为属于B的子区域；二是在形式逻辑矛盾的“是”与“非”之间增加了一个可以亦此亦彼的“临界”区域.因而可拓集合涉及的是：“是”、“临界”、“可拓域”、“非”.所以我们说可拓集合的哲学基础是：形式逻辑矛盾律+临界+可拓域(排中律的替代品).如果说在模糊集合中，扎德是根据“秃子悖论”给出了模糊中介；那么在可拓集合中,或许我们可以说蔡文是根据“罗素悖论”给出了“临界”区域.蔡文也自豪地认为在可拓集合中可避免“罗素悖论”，就像在模糊集合中可以避免“秃子悖论”一样.但需要注意的是扎德的模糊中介并未否定矛盾律而是仅仅放弃了排中律；而蔡文的“临界”区域则是既否定矛盾律又放弃排中律.可拓集合实际上是将讨论域分成三段：一段上严格遵照形式逻辑矛盾命题(普通集合)，一段上的形式逻辑矛盾可以转化为非矛盾(可拓域)，一段上允许有包含形式逻辑矛盾的事物存在(“临界”区域).

例如，用一杆只能称两百斤的秤，要称几千斤重的大象，怎么办？曹冲用船把大象换成等重的石头，用秤称石头而解决了这个问题.但曹冲的办法是不是最佳呢？其实也可以用等重的水、等重的沙、等重的一队人来代替大象，这就是拓展的方法.此外，有人也会想到用木排、竹排代替船，这又是另一种变换.也还可以用跷跷板、大树杈和杠杠等.总之，方案有很多个，必须进行评价，找可行、成本少、耗时小的创意去实施.那么，用什么办法和程序可以找到这些变换呢？这是可拓学研究的核心.可拓学就是研究事物拓展的可能性和开拓创新的规律与方法，并用变换来解决矛盾问题的科学，它是一门横跨哲学、数学与工程学的交叉学科.

4 粗糙集合的哲学基础

有一种观点认为：知识源于人类对物种的分类能力.例如：在某种环境下，机器人表现的像是有知识、有“智慧”，实质上是它们将外部环境和内部状态的传感信号分类，得出可能的情况并由此支配行动，知识直接与真实或抽象世界有关的不同分类模式联系在一起.因此，任何一个物种都是由一些知识来描述的，根据这些知识可以把物种分类，利用物种不同的属性知识描述 ,对物种可以产生不同的分类.基于这种观点，波兰学者Z.Pawlak教授等提出了粗集理论.其概念表述如下：设X是论域U的一个子集，R为其上的一个分类关系，如果X能用R分类，即它可用某些R基本集的并来表示，则X是R可定义的精确集，如果不能，则称X是R粗糙集.所以我们说粗集的哲学基础是:形式逻辑矛盾律+粒边界中介(排中律的替代品).在知识的表达与获取方面，虽然粗集理论和模糊集合理论都是研究信息系统中知识不完善、不准确问题，但它们各自的着眼点不同，粗集理论解决问题的出发点是信息系统中知识的不可分辨性，而模糊集合理论解决问题的出发点是信息系统中知识的模糊性，两者不仅在概念上不能相互替代，在处理方法上也各有特色.粗集具有很强的定性分析能力，它不需要预先给定某些特征或属性的数量描述，如模糊集合理论中的隶属度或隶属函数等，而是直接从给定问题的描述数据出发，通过不可分辨关系和不可分辨类确定给定问题的近似域，从而找出该问题的内在规律.

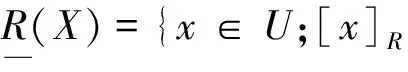
5 反演集合的哲学基础

在哲学中，矛盾分两类：一类是形式逻辑矛盾，另一类是辩证逻辑矛盾.数学中的普通集合和模糊集合等概念是以形式逻辑矛盾为哲学基础的，而反演集合概念则是以辩证逻辑矛盾为哲学基础的.

在形式逻辑中，矛盾概念是指事物肯定性概念(是)和否定性概念(非)之间的矛盾.如：正数与非正数；正电子与非正电子等之间的矛盾.在任意指定的论域中，普通集合涉及的是“是”与“非”，论域中任一元素，或属于该集合，或不属于该集合；模糊集合涉及的是“是”与“非”和“是”与“非”之间中介过渡的模糊区域.论域中任一元素，或百分之百属于该集合，或百分之百不属于该集合，或以百分数的形式归属于中介过渡模糊区域 .

在辩证逻辑中，矛盾概念是指一个事物内部对立的两个侧面,如正、反两面之间的矛盾.如：正数与负数；正电子与负电子等之间的矛盾.以辩证矛盾为哲学基础，我们可以给出一种有别于普通集合和模糊集合、可拓集合、粗糙集合等的新集合——反演集合，其定义如下：

[1]胡宝清.模糊理论基础(第二版)[M].武汉：武汉大学出版社，2010.

[2]蔡文.可拓集合和不相容问题[J]．科学探索学报，1983(1)：83-97.

[3]PawlakZ.Roughsets[J].InternationalJournalofComputerandInformationScience, 1982 (11)：341-356.

[4]王国胤，YaoYY，于洪.粗糙集理论与应用研究综述[J].计算机学报，2009(7)：1229-1246.

[5]刘建忠.反演集合理论及其应用[M],昆明：云南科技出版社，1999.

[6]李道国,苗夺谦,等.粒度计算研究综述[J].计算机科学，2005，32(9)：1-12 .

[7]王健吾.数学思想方法引论[M].合肥：安徽教育出版社，1996.

[责任编辑：王 军]

The philosophical basis and difference of variety of set theory

LIANG Junqi

(School of Mathematics and Statistics,Shangqiu Normal University,Shangqiu 476000,China)

a brief introduction to the general collection of fuzzy sets, extension set and rough set the philosophical basis of set theory, and pointed out that the main difference.

cantor set; fuzzy set; extension set; rough set; philosophical basis; inversion set

2016-04-13

河南省基础与前沿科学技术研究基金资助项目(122300410222);河南省教育厅科学技术研究重点基金资助项目((2011A120007，2012B120011，2014A120008)

梁俊奇(1958—)，男，河南宁陵人，商丘师范学院教授，硕士生导师，主要从事智能计算与不确定信息处理的研究.

TP18

A

1672-3600(2017)06-0013-03