基于Workbench的板弹簧模态及谐响应分析

刘海舟

（北京中航双兴科技有限公司，北京 100010）

基于Workbench的板弹簧模态及谐响应分析

刘海舟

（北京中航双兴科技有限公司，北京 100010）

板弹簧支承技术是直线驱动装置的关键技术之一，其在军事、医疗、超导等领域具有广阔的应用前景。文章采用SolidWorks软件建立板弹簧的三维模型，并基于Workbench对板弹簧进行了模态及谐响应分析，得出了弧弹簧的位移频响曲线，验证了设计要求，为后续结构优化奠定了基础。

板弹簧；模态分析；谐响应分析；直线驱动装置；Workbench

板弹簧支承技术是直线驱动装置的关键技术之一，因其振动噪声小、可靠性高及疲劳寿命长等优点，使得板弹簧在军事、医疗、超导等领域具有广阔的应用前景。目前板弹簧技术广泛应用于大功率声源、地震检波器、冰箱压缩机等产品，本文基于大功率声源的技术背景，采用Workbench软件分析对板弹簧进行分析。

相较于其他形式的弹簧，板弹簧具有良好的径向刚度，作为弹性元件能起到支撑作用，在简化结构的同时又大幅减少了运动系统的质量。将板弹簧这一特性应用于声源中，可降低声源的频响控制与优化的要求，从而确保运动部件具有良好的响应性，实现优质的发声源。但板弹簧的结构形式复杂，各尺寸参数对板弹簧性能的影响不尽相同，且板弹簧不同于普通弹簧具有可量化的经验公式可寻，因此对于板弹簧的设计优化，最理想的手段就是借助于有限元分析。而对板弹簧进行有限元分析最基本的就是模态分析和谐响应分析。

模态分析用于确定板弹簧结构的振动特性，即了解板弹簧的固有频率和振型。对板弹簧进行模态分析可以为结构系统的振动分析、振动故障诊断和预报以及结构动力特性的优化提供依据。谐响应分析是机械结构在承受正弦规律变化的动载荷驱动时的频率响应。进行谐响应分析可帮助设计人员检验结构在受迫振动下克服共振、疲劳及其他影响。

1 模型建立

1.1 工况条件分析

声源要求工作频率范围为10～80Hz，其中在15Hz和70Hz时要求工作位移为±4.6mm，系统的最大推力约为500N，负载质量约为500g，驱动信号为正弦变化。为了能够兼顾两个工作频点，经计算，当弹性系统的固有频率控制在62±1Hz时整体效率最高。系统结构如下图所示，板弹簧的外圈固定，内圈与运动部件采用螺纹连接，运动部件为圆桶状，其内表面与固定结构件外表面采用间隙密封（间隙为0.1mm，即要求运动部件配合公差及径向跳动均不大于0.1）。板弹簧对运动部件起到支撑作用，要求在工作过程保证运动部件的运动稳定性并控制运动部件的径向跳动。作为弹簧元件板弹簧是动力系统的储能器，要求通过调节板弹簧，使弹性系统的一阶固有频率能够满足工作频率范围内不同频点的位移要求，高阶固有频率尽可能远离工作频率范围，同时包含板弹簧的弹性系统应兼具对声源降噪、滤波的作用。

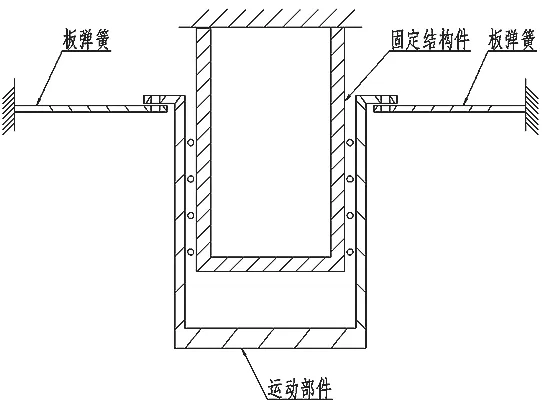
图1 运动部件结构示意图

1.2 三维模型

本例采用SolidWorks软件进行三维建模，将模型通过IGS模式导入Workbench软件。在下面的运动部件示意图（图2）中不难发现板弹簧的内、外圈均采用面接触、螺纹固定的方式，系统的驱动力通过运动部件传递至弹簧内圈。为了减小仿真计算的工作量，提高计算效率，对仿真模型进行如下简化及假设：（1）板弹簧的内、外圈固定处均为刚性连接，与内、外圈的配合表面均为有效贴合，驱动力不会致使板弹簧之外的其他结构产生变形；（2）运动部件为刚件，在振动过程中不会产生位错、变形，驱动力可以直接作用至板弹簧内圈处；（3）仿真计算中忽略运动部件自身质量产生的惯性力和空气摩擦阻力，即板弹簧受迫力只有驱动力。

图2 运动部件示意图

图3 板簧示意图

板弹簧所用材料为65Mn弹簧钢，密度为ρ＝7.85×kg/m3，弹性模量：E＝2.06×EPa泊松比μ＝0.3，曲服强度380MPa。

2 模态分析

2.1 模态分析的理论基础

模态分析是板弹簧振动分析的基础，它只受板弹簧自身的结构特性和材料特性的影响，与外部条件无关。模态分析的核心内容是准确描述结构系统的模态参数，根据D.Alembert原理，将弹性体的动力学问题简化为静力学问题。固有频率可通过固有角频率得到。所以提高固有频率可以提高板弹簧的单位质量刚度，同时使板弹簧的动态性能随之提高。

2.2 网格划分及施加约束

Workbench中提供自动和手动划分两种划分方法，本文采用手动与自相结合的方式对板弹簧进行网格划分。对整体模型采用自动划分的方式，局部细节采用手动方式调整，从而实现重点分析关键部位且减少不必要的计算量。

2.3 求解及结果分析

运用Workbench对板弹簧进行模态计算，得出其前十二阶模态频率及振型。可以看出，随着模态阶数的提高，振型也越来越复杂。自第二阶开始，板弹簧便不再展现出单方向受迫振动的特征，转而出现了局部的扭转变形。随着阶数的增加，这种扭转愈发明显，至最高阶（所取最大阶数）时，六个支臂全部出现扭转，而板弹簧整体以波浪形式变形。高阶振型的复杂化也将导致板弹簧变形的离散化，从而增加装置工作的不确定性。除此之外，当阶数较低时，板弹簧的最大变形区域处于载荷施加部位，是较理想的变形结果，当阶数较高时，板弹簧的最大位移处于支臂的前端，经疲劳强度分析此处也是疲劳强度最为集中的区域，属于不理想的振型。结构设计中应通过改变结构参数或调整阻尼参数避免这类情况的发生。

3 谐响应分析

谐响应分析是一种频域分析，用于确定结构在已知频率和幅值的正弦载荷作用下的稳态响应。由于本文中板弹簧所受驱动载荷为正弦变化，因此谐响应分析恰能反映板弹簧的受迫振动情况。

3.1 载荷及约束

如前文所述板弹簧的外圈与声源结构件固定，所以将边界约束条件设置在板弹簧的外圈螺纹孔处。约束方式为固定约束。

载荷：板弹簧的驱动载荷通过运动部件传递至板弹簧的内圈部分，运动部件与板弹簧连接方式为螺纹连接。所以载荷的加载位置为内圈处的螺纹孔。驱动力为正弦信号载荷、载荷大小为100N。载荷方向为轴向。如图4为板弹簧的载荷及约束示意图：

图4 板弹簧载荷及约束示意图

3.2 求解及结果分析

在本文中，设定模态分析的间隔频率为30Hz，分析范围为0～300Hz，不考虑结构阻尼，得到聚焦于载荷作用面上的分析结果，在此罗列出板弹簧的总变形、轴向的等效变形以及频率响应进行分析。为保证覆盖板弹簧的有效工作区间的同时减少非必要计算量，选取前10阶进行谐响应分析，最终结论如下：（1）板弹簧的总变形在不同频点处的差别较大（最大总变形为120Hz时的5.9279mm），但此处的变形量并非发生在指定方向上，对比模态分析结果后可以看出变形方向在不同频率点处有明显变化，这会直接影响指定方向上的等效变形，板弹簧的轴向等效变形在120Hz时的变形量为2.3397mm，这与最大总变形的差距明显，这说明板弹簧在该频率点处不再沿着载荷施加方向进行单纯的受迫变形，而是激振出了其他频点处的变形；（2）弹簧的固有频率位于120Hz处，在120Hz附近由于产生了结构共振，在相同驱动力作用下板弹簧会产生较大的位移变形。但由于相位角的变化，在指定方向的变形量与总变形量存在着较大的“差值”。而这些“差值”对于整体结构而言是有害的，可能造成装置的连接松动或对其他配合结构件产生破坏作用，所以对此情况要慎重对待。

图5 板弹簧总变形云图

图6 板弹簧轴向等效变形云图

4 弹性系统固有频率分析

文中所做模态及谐响应分析的目的在于通过了解板弹簧自身的振动特性，经过计算推导得出弹性系统的固有频率，从而确定是否满足设计要求。本弹簧不同于普通弹簧，其刚度值为变量，图7为板弹簧的刚度曲线。计算固有频率时选取基频（一阶）的刚度进行计算。

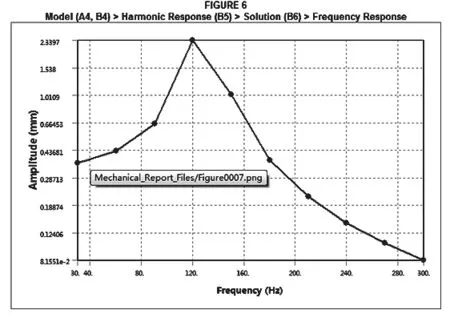
图7 板弹簧刚度曲线图

经过计算文中弹性系统的固有频率f＝60.7Hz，而这一结果也与实验结果基本吻合。

5 结语

（1）运用Workbench对板弹簧进行模态分析，得出了其前10阶的模态分析图，通过分析为后续的谐响应分析提供了参数和指导；（2）对板弹簧进行谐响应分析，根据响应频率曲线可以分析得出其低阶对模态对弹簧的动态影响较大；（3）板弹簧的固有频率处会产生较大的形变，在装置设计过程中要合理选择装置的工作频率及整体装置的共振频点，尽可能远离弹簧的固有频率。

[1]陈楠，陈曦，吴亦农．圆渐开线涡旋柔性弹簧的制造方法：中国，CN1751822[P]．2005.

[2]Gaunekar A S，Goddenhenrich T，Heiden C．Finite elementanalysis and testing of flexure bearing elements[J]．Cryogenics，1996，（36）.

[3]袁重雨，陈曦，刘颖，祁影霞．三种不同型线柔性弹簧的有限元分析及对比研究[J]．低温与超导，2011，（7）.

[4]高威利，陈国邦，汤珂，颜鹏达．涡旋板弹簧的有限元分析及实验[J]．低温与超导，2009，（9）.

（责任编辑：蒋建华）

TH213

1009-2374（2017）07-0091-02

10.13535/j.cnki.11-4406/n.2017.07.042

刘海舟（1986-），男，河北衡水人，北京中航双兴科技有限公司工程师，研究方向：机电工程。

A