遗传算法在土坡滑动面搜索和稳定性评价中的应用

王 军

(湖南工程学院 建筑工程学院，湘潭 411104)



遗传算法在土坡滑动面搜索和稳定性评价中的应用

王 军

(湖南工程学院 建筑工程学院，湘潭 411104)

针对土质边坡滑面的特点，分析了遗传优化算法在边坡滑动面搜索和稳定性评价的有效应和合理性.通过改编的简易遗传算法程序对高陡土质边坡进行计算，结果显示：遗传算法搜索得到的圆弧滑动面的半径值介于Bishop法和有限差分法之间，同样安全系数值也介于两种方法之间，说明了遗传优化算法应用于土质边坡的滑动面搜索和稳定性评价是可行的，该结论能为土质边坡的稳定性评价和工程加固提供借鉴.

土质边坡；遗传算法；滑动面；稳定性

0 引言

土质边坡在深基坑开挖、路基填挖、库坝堆土、地下空间建设等工程中大量存在，具有技术难度高、管理复杂、灾害隐患多等特点，是岩土科技人员研究的重点对象之一.目前，关于土质边坡的研究热点集中在边坡滑动面的搜索、安全系数的计算及稳定性评价和工程加固等方面，其中边坡滑动面的搜索又是边坡工程后续工作的前提条件，在工程实践和科学研究中得到重视，已取得了许多研究成果[1,2].

土质边坡滑动面的确定方法大都根据工程经验和极限平衡理论，通常认为粘性土边坡为圆弧滑动面，非粘性土边坡为直线滑动面，此结论已在工程界得到了大量应用[3,4].但是该方法假定条件太多，研究人员主观性强，又缺乏理论支持，因此这样得出的滑动面与边坡现实稳定状况有一定的出入，所得结果有其局限性.数值分析方法能够得到边坡结构的应力、应变和塑性区等关键量的分布特征，并且根据贯通的塑性区可以获得边坡的潜在滑动面和安全系数.但是数值分析方法技术难度高、程序收敛难以控制，甚至出现局部收敛情况，又不便于被广大技术人员所掌握和应用，因此应用上受到局限.优化算法具有全局搜索功能，假定条件下少、参数容易获取，可以准确地获得边坡潜在滑动面，同时能够对边坡进行稳定性评价，目前已在工程和学术界得到了有效应用.遗传算法是最优化算法之一，操作简便，物理意义明确，能够获取复杂土质边坡的滑动面，能为边坡稳定性评价和工程加固提供指导[5-6]，但是相关方面的文献资料不多见，为此笔者结合改编的遗传算法简易程序和算例，研究该方法在土坡滑动面搜索和稳定性评价中的可行性.

1 滑动面搜索

1.1 直线滑动面

直线滑动面一般是针对简单的无粘性土均质土坡，由于无粘性土颗粒主要以克服内摩擦角为主，粘结力比较弱，因此只要边坡土体单元是稳定的，则该土质边坡就处于整体稳定状态.

无粘性土边坡的整体安全系数为抗剪力(抗剪强度)与剪切力之比，即

(1)

式中，Tf为抗剪力，T为剪切力，φ为边坡土体的内摩擦角，α为边坡坡角.

从上式可以看出，无粘性土边坡的整体安全系数只与土体的内摩擦角和边坡坡角的比值有关，当边坡坡角小于内摩擦角时，边坡就处于稳定状态；当安全系数为1时，边坡就处于极限平衡状态，此时得到的坡角就为临界边坡角；当安全系数小于1时，边坡就失稳.因此，直线滑动面的搜索过程是最简单的.

1.2 圆弧滑动面

现实土质边坡工程中，边坡的滑动面型式主要是曲线滑动面，如对数螺旋线、圆弧滑动面、椭球面、抛物线等型式，其中圆弧滑动面应用最为广泛.然后根据假定的滑动面，运用垂直条分法求解安全系数来评价边坡的稳定性.

2 遗传算法搜索土质边坡滑动面

遗传全局优化算法是基于二进制编码技术，将求解问题具体为种群，根据种群中每个个体的优劣信息进行全局搜索，得到全局最优解[7].遗传算法在搜索土质边坡滑动面的应用过程中，其计算流程如下：

(1)根据土质边坡的计算边界、初始条件和土体的物理力学参数，确定遗传算法计算参数，确定边坡滑动面搜索种群Nyd，变异概率Pm，交叉概率Pc和变异概率Pv以及最大进化代数Tmax.

(2)以初始进化代数，即t→0，在求解变量的计算范围内，随机产生Nyd个体，令为搜索滑动面的初始种群P(0).

(3)建立土质边坡整体安全系数的目标函数值，并进行遗传操作，即滑动面搜索.

(4)计算土质边坡群体P(t)中所有个体的适应度值，根据个体的适应度值进行评价和取舍.

(5)根据个体的适应度和评价结果，用比例选择法对所列个体进行选择操作，完成选择过程.

(6)结合遗传选择操作结果，对该种群中的每个个体 以较小的变异概率pm进行变异操作.

(7)再将种群中的个体进行随机配对，并对每个个体以交叉概率pc完成交叉操作.

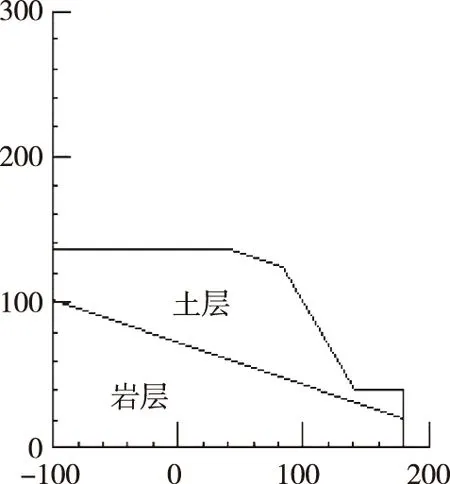
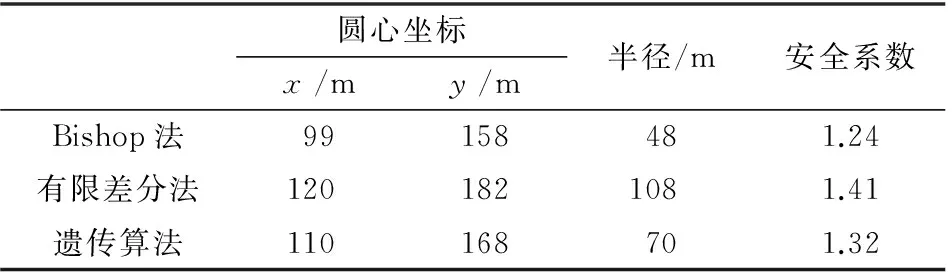
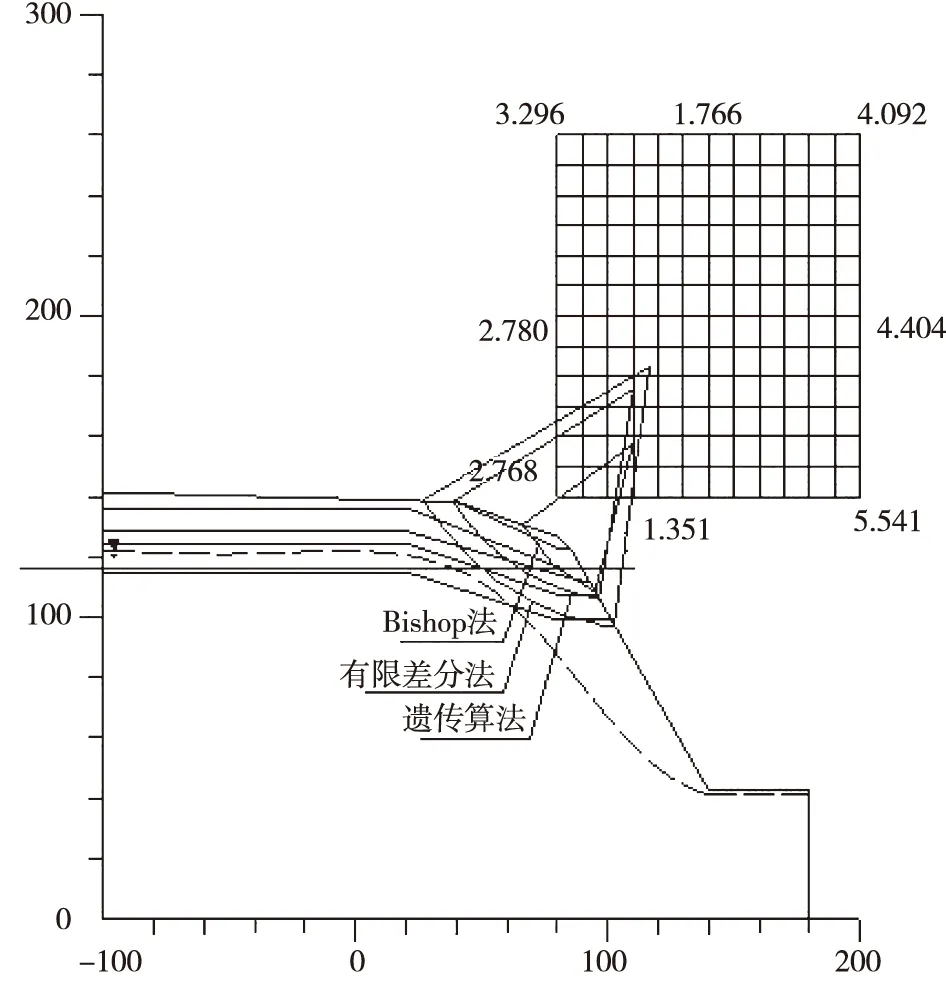
(8)当进化代数t

3 算例分析

为了验证遗传全局算法的有效性和合理性，文中选取一非均质土质边坡，该边坡主要由上部的土体和下面的岩层组成，边坡的高度为128m，宽度为280m，边坡坡角在45°以上，属典型的高陡土质边坡，为便于与传统极限平衡法和有限差分分析法进行比较，令岩层完整性好，边坡的整体稳定性主要表现在土体部分.计算过程中外荷载主要为土体自重，不考虑地震、地下水和施工的影响.其计算范围如图1所示，物理力学参数如表1所示.

表1 物理力学参数

图1 计算范围(单位：m)

(1)Bishop法搜索边坡滑动面

Bishop法是最常用的极限平衡法之一，已在边坡工程中得到了大量的应用.文中通过该方法搜索的滑动面、圆弧半径、圆心位置和最小安全系数结果如表1所示，滑动面的搜索型式如图2所示.

(2)有限差分方法搜索边坡滑动面

有限差分法是充分利用现代计算技术，将求解区域划分为有限差分单元，根据边界条件和初始条件进行程序计算，可以得到应力、应变、塑性区等有用量的分布情况，限于研究主题其分布特征不再阐述.文中运用平面有限差分法获得了该土坡的滑动面和安全系数值，计算结果如表1所示，滑动面的搜索型式如图2所示.

(3)遗传算法搜索边坡滑动面

根据遗传算法的计算流程，运用改编的简易遗传算法计算程序对该土质边坡的潜在滑动面进行了全局搜索和安全系数的求解，计算结果如表2所示，滑动面的搜索型式如图2所示.

表2 滑动面的搜索结果

从表2和图2可以看出，有限差分法计算得到的滑动面半径值为最大，Bishop法得到的滑动面半径值为最小，遗传算法通过全局搜索得到的滑动面半径值介于两方法之间，并且安全系数也介于两方法之间.以上计算说明了遗传优化算法应用于土质边坡的滑动面搜索和稳定性评价是有效的，合理的，能为边坡工程实践和科学研究提供借鉴.

图2 土质边坡滑动面的搜索

4 结论

(1)土质边坡的滑动面型式在工程中主要呈现圆弧型，不完全满足工程经验认为的粘性土边坡为圆弧滑动面，非粘性土边坡为直线滑动面的假定.

(2)笔者建立了遗传算法搜索土质边坡滑动面的计算流程，结合高陡土质边坡算例计算得到遗传算法通过全局搜索得到的滑动面半径值介于Bishop法和有限差分法之间，同样安全系数也介于两方法之间，说明了遗传优化算法应用于土质边坡的滑动面搜索和稳定性评价是有效的、合理的.

[1] 朱大勇，钱七虎.三维边坡严格与准严格极限平衡解答及工程应用[J]. 岩石力学与工程学报，2007，26(8)：1513-1530.

[2] 程良奎.岩土锚固的现状与发展[J].土木工程学报,2001,34(1):7-12.

[3] 陈祖煜.土质边坡稳定分析(第一版)[M].北京：中国水利水电出版社，2003.

[4] 王成华，夏绪勇.边坡稳定分析中的临界滑动面搜索方法述评[J].四川建筑科学研究，2002，28(3)：34-39.

[5] Goldberg D E. Genetic Algorithms in Search, Optimization and Machine Learning[M].Addison-Wesley Professional，1989.

[6] 解可新，韩立兴，林友联.最优化方法(第一版)[M]．天津：天津大学出版社，1997.

[7] 王小平，曹立明．遗传算法——理论、应用与软件实现(第一版)[M].西安交通大学出版社，2002.

Application of Genetic Algorithm to Search Slipping Surface and Stability Evaluation on Soil Slope

WANG Jun

(College of Architecture Engineering, Hunan Institute of Engineering, Xiangtan 411104, China)

In view of the character is tics of slipping surface on soil slope, genetic algorithm is applied to search slipping surface and to obtaining safety factor, which is effective and reasonable for soil slope. The modified program is used to analyze the instance, which is used on high steep and two layer medium. The results show radius and safety factor on soil slope are middle between Bishop method and finite different method by genetic algorithm and can direct stability evaluation. So the conclusion can offer guidance for engineering application.

soil slope; genetic algorithm; slipping surface; stability

2016-11-18

湖南省自然科学基金项目(2015JJ4019)；湖南省教育厅优秀青年资助项目(13B016).

王 军(1978-)，男，博士，副教授，研究方向：土木工程.

TS106.6

A

1671-119X(2017)02-0059-03