考虑桩土相互作用的连续刚构桥抗震性能分析

胡 迪，陈锐林，张 超，夏祥忠，邓小波

(湘潭大学 土木工程与力学学院，湘潭 411105)



考虑桩土相互作用的连续刚构桥抗震性能分析

胡 迪，陈锐林，张 超，夏祥忠，邓小波

(湘潭大学 土木工程与力学学院，湘潭 411105)

为研究大跨径连续刚构桥的静、动力特性及抗震性能，以某(65+110+65)m预应力混凝土连续刚构桥为工程背景，采用MIDAS Civil建立全桥有限元分析模型，计算不同荷载作用下主梁特征截面的剪力、弯矩和应力.结合反应谱法和时程分析法进行地震反应分析,对该桥抗震性能作出评价.结果表明：结构重力和预应力一次效应引起的内力占主要因素，主梁各截面应力均能满足规范要求；第1阶振型表现为主梁纵向漂移，桥墩纵向振动的模态，表明该桥顺桥向刚度较横桥向弱；比较成桥阶段与最长悬臂阶段桥墩关键位置处的地震作用，结构抗震性能需考虑的地震作用方向不同；地震作用下,桥墩强度和变形满足设计规范要求，结构动力特性及抗震性能良好.

连续刚构桥；桩土相互作用；动力特性；反应谱法；时程分析法；抗震性能

预应力混凝土刚构桥具有外形美观，结构尺寸小，桥下净空大，桥面行车平顺等特点，近年来较多的应用在城市桥梁中[1].刚构桥是一种主梁与桥墩固结的结构体系.在竖向荷载作用下，刚构桥中梁与支座刚接的部位会产生负弯矩，从而减少跨中弯矩，达到减少梁体截面尺寸、增大桥梁跨度的作用[2].然而，对于地震作用下的高墩大跨连续刚构桥，因采用墩梁固结，其抗震特性与普通梁式桥存在明显差异[3].自GB 18306-2001实施以来，2008年汶川8.0级地震、2011年日本东部海域9.0级地震等国内外地震灾害事件为地震构造环境和地震活动特征取得新的认识，本文参考GB 18306-2015《中国地震动参数区划图》对连续刚构桥的抗震设防进行相应研究.

郑史雄等[4]研究了地震波的相位差和地基土层性质对刚构桥的地震反应影响.朱东生等[5]探讨了墩与主梁之间不同联结方式、曲率半径等因素对曲线连续梁桥地震反应的影响.牛俊武[6]采用时程分析方法，研究了地震波和主梁参数对高墩大跨连续刚构桥的动力响应.李茜，王克海等[7]采用反应谱法、时程分析法对连续-刚构组合梁桥与连续刚构桥的地震响应进行分析，并考虑桩-土相互作用对高墩桥梁地震响应的影响.陈敏海[8]研究了行波效应对连续刚构桥的地震反应影响.侯鹏飞[9]讨论了墩高变化对大跨度连续刚构桥动力特性的作用.付春辉[10]分析了考虑和不考虑桩基桩-土之间的相互影响对连续梁桥的动力特性和抗震性能的影响.T.Miki，J.Niwa[11]对高架连续刚构桥采用三维格子法进行非线性的地震响应分析，并与实际地震时的破坏形态进行对比.Sung Jig Kim，Curtis Holub等[12]研究了水平方向及竖向组合地震作用和单一水平向地震作用对桥墩的影响.Guirguis，Mehanny[13]根据欧洲规范对具有不同高差桥墩的三跨连续梁桥进行非线性时程与静力弹塑性分析.

地震区的桥梁结构选型应首先进行动力概念设计，随后是结构抗震的能力分析—强度与位移控制(延性设计).在桥梁抗震计算中，早期采用简化的静力法，50年代后发展了动力法的反应谱理论，近20年来对重要结构物采用动力法的动态时程分析法[14].笔者以一座典型的三跨预应力混凝土连续刚构桥为例，考虑桩-土-结构相互作用效应，根据实际施工情况划分施工阶段，建立空间有限元模型进行结构静动力特性计算分析.然后按照设计地震烈度对其进行地震反应谱分析和时程分析，得到E2地震作用下的地震响应.并将两种方法计算得到的响应值进行差异比较，研究该桥的动力特性及抗震性能.

1 工程概况

某工程为一座65 m+110 m+65 m的三跨预应力混凝土变截面连续刚构桥(见图1)，左、右行分离，单幅桥宽12.5 m.桥墩采用钢筋混凝土实心墩、钻孔灌注桩基础，采用主梁悬臂浇注施工方法.

图1 主桥跨径布置示意图

主桥采用单箱单室直腹板箱型断面，三向预应力钢筋混凝土结构，箱梁顶板宽12.5 m，底板宽6.5 m，翼缘板悬臂长3.0 m；支点处梁高6.5 m，现浇段及合拢段梁高2.8 m；0号块底板厚1.0 m，现浇段及合拢段厚0.3 m，梁高及底板厚度均按2次抛物线变化.箱梁顶板厚度：除梁端支承截面为0.8 m外，其余梁段厚0.3 m.箱梁腹板宽度：墩身范围内0号块由1 m按线性变化到0.75 m，梁高变化段截面等宽0.75 m，合拢段宽0.45 m，梁端支承截面宽1.25 m，其间部分按线性变化.

2号、3号桥墩采用双肢薄壁墩，墩顶与上部箱梁固结，墩高分别为19.92 m、21.90 m.桥墩横桥向宽6.5 m，顺桥向长1.2 m，外设半径为7.5 cm的倒圆角.墩承台厚3.5 m；平面尺寸为8.2 m×7.0 m.桥墩采用钻孔灌注桩基础，单幅每墩采用4根直径为2.0 m的桩基础.

2 有限元模型

本文采用MIDAS Civil(8.32)建立该桥的三维有限元计算模型(如图2所示)，参照施工阶段梁段的划分与预应力钢束的布置，并考虑桥梁的实际情况，将全桥共离散为415个节点、392个单元.主梁采用变截面空间梁单元模拟，主墩、承台和桩基采用一般梁单元模拟，预应力钢束通过预应力荷载进行施加.支座采用弹性支承等代弹簧模拟，墩梁固结采用弹性连接中的刚性连接，按照规范采用等代土弹簧模拟桩基与土的相互作用[15].模型中，各构件的材料特性、边界条件以及连接方式均按实际情况确定，力求真实地反映实际结构的力学性能.模型参数取值为：主梁混凝土强度等级C50，弹性模量E=3．45×104MPa；桥墩混凝土强度等级C40，弹性模量E=3．25×104MPa；承台和桩基混凝土强度等级C30，弹性模量E=3．0×104MPa；三种强度等级的混凝土泊松比均为0．2，容重为25kN/m3；重力加速度g=9．81m/s2.

图2 刚构桥有限元模型

3 静动力特性分析

3.1 静力特性分析

本文主要从这剪力、弯矩以及应力这3个方面分析主梁在荷载作用下的受力特性，其中结构物自身重力及桥面铺装、附属设施等外加重力均属于结构重力[16].

主梁在荷载作用下的剪力图如图3所示，其中结构重力与预应力一次效应产生的剪力占主要因素，汽车荷载引起的剪力相对较小；预应力一次效应在边跨跨中、靠墩顶截面处和中跨跨中引起的剪力分别占结构重力的-54.04%、116.80%和57.05%，在设计过程中，应注意跨中截面处剪力对结构受力的影响，验算相应截面的抗剪承载力.

主梁在荷载作用下的弯矩图如图4所示，从图中可以看出，结构重力与预应力一次效应产生的弯矩占主要因素，两者引起的弯矩方向相反，汽车引起的弯矩相对较小；预应力一次效应在边跨跨中、靠墩顶截面处和中跨跨中引起的弯矩分别占结构重力的-48.25%、-63.17%和-201.82%，因此在设计过程中进行预应力钢束布置时，应考虑预应力一次效应对结构受力的影响.

图3 主梁在荷载作用下的剪力

图4 主梁在荷载作用下的弯矩

主梁的强度及应力直接关系到成桥运营阶段安全，计算过程中考虑的荷载包括：自重、预应力、施工临时荷载、二期荷载、温度荷载、活载等，并考虑了预应力损失以及混凝土的收缩徐变引起的内力变化的影响.依据《公路桥涵设计通用规范》(JTG D60-2015)，对主梁PSC截面的使用阶段正截面压应力、使用阶段斜截面主压应力按最不利荷载组合进行验算，由图5、图6可知：主梁正截面最小压应力为2.72 MPa、最大压应力为13.29 MPa，按文献[17]第7.1.5条规定，求得容许压应力为16.2 MPa；主梁斜截面最小压应力为2.56 MPa、最大压应力为13.49 MPa，按文献[17]第7.1.6条规定，求得容许压应力为19.44 MPa.结果表明，主梁各截面应力均能满足规范要求，结构运营状态安全.

图5 使用阶段正截面压应力验算

图6 使用阶段斜截面主压应力验算

3.2 动力特性分析

结构模态分析是动力分析的基础，在结构动力分析中，将静力位移法做动态处理，因此土抗力系数取值也通常比静力状态下大，按文献[12]地基系数一般取m动=(2～3)m静，本文取2.5.采用多重Ritz向量法进行桥梁的动力特性分析，为使所考虑的振型阶数应在计算方向获得90%以上的有效质量，在此考虑前120阶振型.限于篇幅，仅列出前10阶振型，并描述了相应的振型形状，结构自振特性如表1所示.

表 1 桥梁自振频率和振型特征

由表1可以看出，结构的基频为0.510Hz，周期为1.960s.前10阶振型特性主要表现为主梁纵向飘移、横向弯曲振动和竖向弯曲振动，且各阶次振动形态比较单一，互不耦合，反映了连续刚构桥结构体系的一般特性.第1阶振型表现为主梁纵向漂移，桥墩纵向振动的模态，表明该桥顺桥向刚度较横桥向弱.

4 抗震性能分析

4.1 反应谱分析

根据本项目安评报告，该桥抗震设防烈度为7度、地震动峰值加速度0.15g，B类桥梁[18]分区特征周期为0.40s, Ⅱ类场地类别.根据《抗震细则》的9.3.6条规定：“混凝土梁桥、拱桥的阻尼比不宜大于0.05”，因此可取阻尼比为0.05.按《抗震细则》6.1.3，本桥属于非规则桥梁，E1地震作用抗震分析可采用多振型反应谱法，水平设计加速度反应谱拟合相关参数见表2.

表2 反应谱拟合相关参数表

采用《公路桥梁抗震设计细则》规范反应谱进行分析，水平设计加速度最大值Smax由下式确定：

Smax=2.25CiCsCdA

(1)

式中：Ci为抗震重要性系数；Cs为场地系数；Cd为阻尼调整系数；A为水平向设计基本地震动加速度峰值.

由式(1)算得E1地震作用Smax=0.145g，E2地震作用Smax=0.439g.同时考虑了顺桥向、横桥向和竖向的地震作用，采用CQC方法进行各振型的组合，地震作用分量组合采用SRSS法计算.仅考虑顺桥向、横桥向两个方向的地震作用.

4.2 线性时程分析

根据桥址处具体场地条件，在已有强震记录中选用修正后的Sfs_48_w、Sun_ns_w、tar_360_nor三条地震波进行时程分析,这3条波特征周期与场地特征周期相近，均适合于Ⅱ类场地类型.3条地震波的有效峰值加速度分别为0.376g、0.078g、0.949g，E1地震作用下，3条地震波的水平方向峰值调整系数分别为：0.172、0.822、0.068.E2地震作用下，3条地震波的水平方向峰值调整系数分别为：0.519、2.490、0.206.动力时程分析时，以恒载为初始状态，考虑了顺桥向、横桥向两个方向的地震作用.图7～图9仅给出E2地震动水平时所使用的地震波数据.

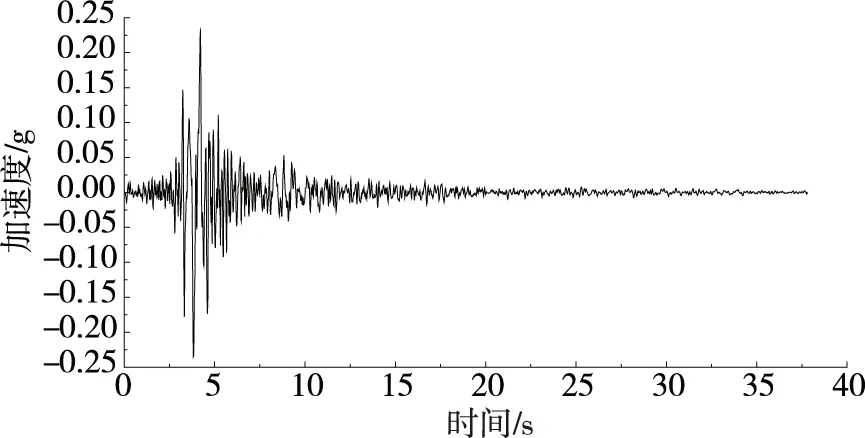
图7 调整后的Sfs_48_w地震波

图8 调整后的Sun_ns_w地震波

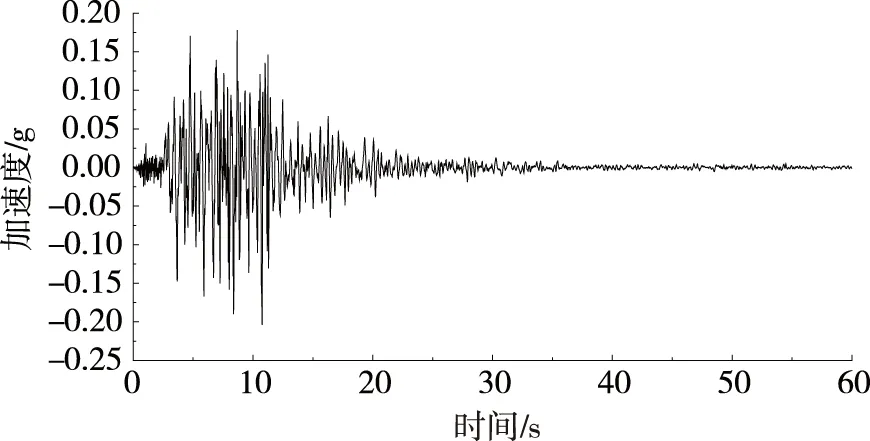
图9 调整后的tar_360_nor地震波

4.3 E1、E2地震作用下的分析结果

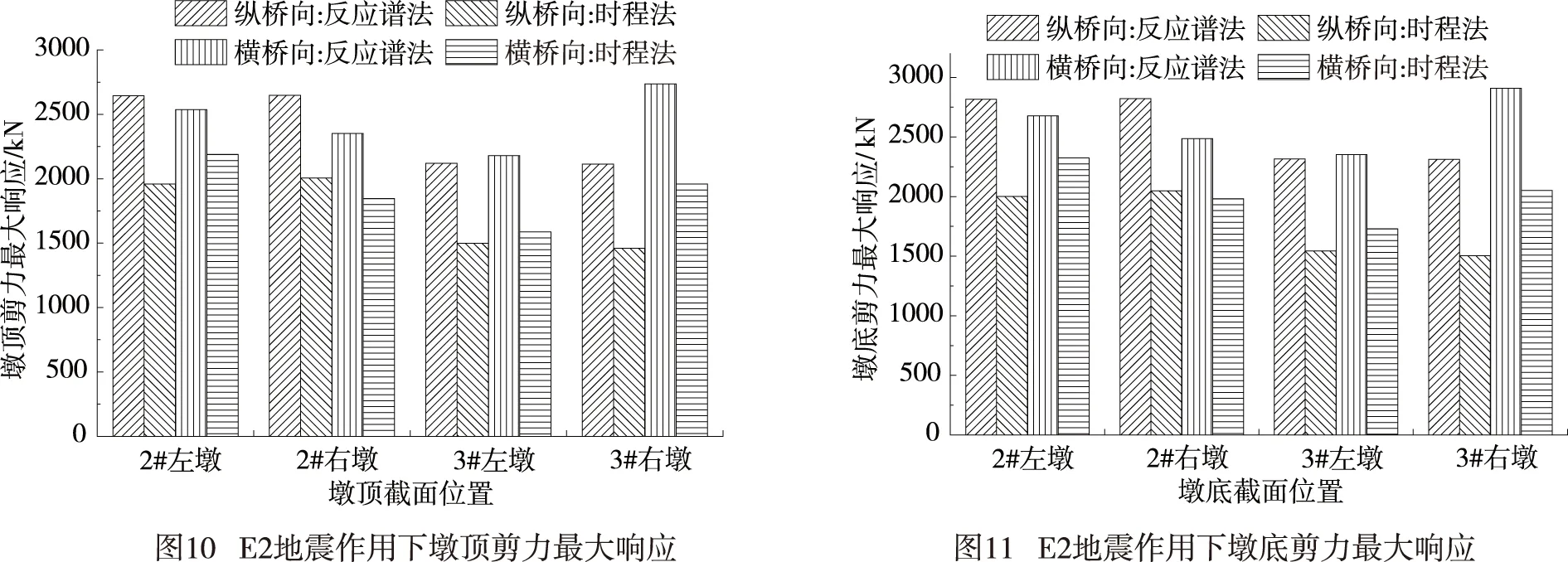
采用反应谱法和线性时程分析法对该连续刚构进行了地震响应分析，各墩墩顶和墩底在E2地震作用下的剪力值(如图10～图11所示)和弯矩值(如图12～图13所示)，其中时程分析法的计算结果取三条地震波对结构作用效应的最大值.由图10～图13比较分析可知：采用反应谱法计算所得结构的剪力和弯矩最大响应值均大于时程分析所得的结果，但两种分析方法所得结果的规律趋势一致，所占比例稍有差异.其中纵向地震作用下，时程分析法所得剪力值占反应谱法的65.1%～75.7%，弯矩值占65.1%～92.6%；横向地震作用下，时程分析法所得剪力值占反应谱法的70.5%～86.8%，弯矩值占70.7%～87.3%.说明采用反应谱法分析比线性时程法分析对该桥梁结构更为不利，因此，建议采用反应谱法对该桥进行抗震设计和验算.

4.4 最长悬臂段地震响应分析

连续刚构桥的整个施工阶段经历了3次结构体系变化，从桥墩施工阶段的独柱结构到悬臂施工阶段的T形结构以及最后成桥阶段的门式框架结构.连续刚构桥的抗震性能相对其他桥型优越，但合拢前的T结构是其最危险的时期，地震的影响易对桥墩的墩底和墩梁结合部位造成损害.该桥的2、3号桥墩以及上部结构的施工形式相同，只是墩高稍有差别，限于篇幅，本节只对墩高21.90 m的2号桥墩最长悬臂段作为研究对象.根据现有桥涵抗震设计规范，对该桥的最长悬臂阶段和成桥阶段的墩梁结合处及桥墩墩底在各方向上所引起结构的剪力、弯矩进行E2地震作用下反应谱对比分析.其中施工阶段考虑了自重、挂篮荷载和预应力荷载，成桥阶段考虑了自重、二期荷载和预应力荷载.

如图14和图15所示，3号桥墩在顺桥向地震作用下，施工最长悬臂阶段的剪力比成桥阶段减少14.9%～15.2%，弯矩减少8.9%～19.7%；而在横桥向地震作用下，施工最长悬臂阶段的剪力比成桥阶段增加0.3%～21.5%，弯矩增加16.7%～38.3%.说明在成桥阶段3号桥墩关键位置处的剪力、弯矩主要由顺桥向地震作用引起，此阶段更需要考虑顺桥向抗震；在施工过程中的最长悬臂阶段3号桥墩关键位置处的剪力、弯矩主要由横桥向地震作用引起，而此阶段更需要考虑横桥向抗震.因此该连续刚构桥梁施工过程中不同阶段，对结构的抗震性能所考虑的地震作用方向有所不同.

4.5 抗震性能评价

工程抗震设防标准的确定既要保证桥梁的抗震安全性，又不致使造价增加太多，使其在经济与安全之间合理平衡，这是桥梁抗震设防的合理原则.

一般情况下，桥梁梁体在E1地震作用下的强度是足够的，因此抗震设计中一般不需要进行梁体强度的验算.而桥墩一般是地震中的薄弱部位，须对桥墩的压弯强度和抗剪强度进行验算[19].计算结果按E2地震作用效应和永久作用效应进行组合，取其荷载效应组合的最大值作为最不利荷载，验算该桥的桥墩强度.本文仅给出顺桥向墩底截面的抗弯、抗压和抗剪验算(如表5所示).由表5可知，在E2地震作用下桥墩强度验算满足现行设计规范要求，结构处于弹性工作状态.E2地震作用下桥墩墩顶位移验算结果如表6所示，由表可知，墩顶顺桥向、横桥向位移在容许范围内，结构动力特性及抗震性能良好.

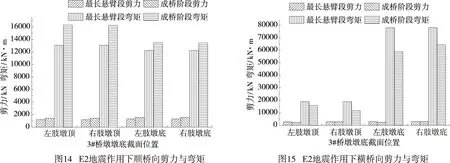
表5 地震作用+恒载作用下桥墩强度验算

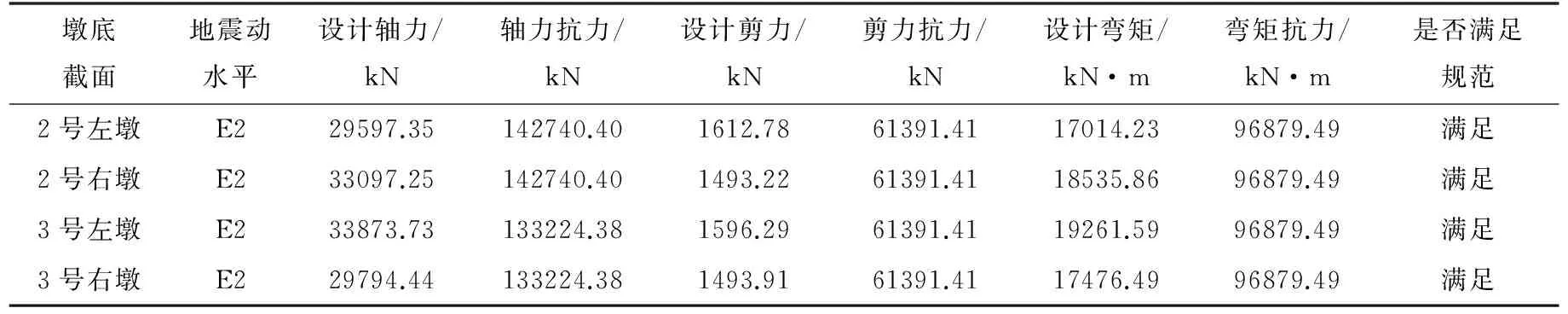
墩底截面地震动水平设计轴力/kN轴力抗力/kN设计剪力/kN剪力抗力/kN设计弯矩/kN·m弯矩抗力/kN·m是否满足规范2号左墩E229597.35142740.401612.7861391.4117014.2396879.49满足2号右墩E233097.25142740.401493.2261391.4118535.8696879.49满足3号左墩E233873.73133224.381596.2961391.4119261.5996879.49满足3号右墩E229794.44133224.381493.9161391.4117476.4996879.49满足

表6 E2地震作用下墩顶位移验算

5 结论

本文对三跨预应力混凝土连续刚构桥静动力特性及地震反应进行分析，并对抗震性能作出评价，主要得出结论如下：

(1)结构重力和预应力一次效应引起的内力占主要因素，在结构设计时应特别注意墩顶附近处及跨中截面内力的验算；主梁各截面应力均能满足规范要求，结构运营状态安全.

(2)该连续刚构桥的自振基本周期为1.960 s，第1阶振型表现为主梁纵向漂移，桥墩纵向振动的模态，表明顺桥向刚度较横桥向弱.

(3)该桥采用反应谱法分析比线性时程法分析所得的结果对结构更为不利，因此，建议采用反应谱法对该桥进行抗震设计和验算.

(4)成桥阶段3号桥墩关键位置处的剪力、弯矩主要由顺桥向地震作用引起，此阶段更需要考虑顺桥向抗震；在施工过程中的最长悬臂阶段3号桥墩关键位置处的剪力、弯矩主要由横桥向地震作用引起，而此阶段更需要考虑横桥向抗震.

(5)在地震作用效应和永久作用效应进行最不利荷载组合下，桥墩验算强度满足现行设计规范要求，结构处于弹性工作状态；墩顶顺桥向、横桥向位移在容许范围内，结构动力特性及抗震性能良好.

[1] 王文涛. 刚构-连续组合梁桥[M].北京：人民交通出版社,1997:96-100.

[2] 陈 全. 高墩大跨连续刚构桥抗震影响因素研究[D]. 成都:西南交通大学硕士学位论文,2013.

[3] 牟德健. 高墩大跨连续刚构桥抗震性能分析[D]. 重庆:重庆大学硕士学位论文,2012.

[4] 郑史雄,奚绍中,杨建忠. 大跨度刚构桥的地震反应分析[J]. 西南交通大学学报,1997(6):14-20.

[5] 朱东生,刘世忠,虞庐松. 曲线桥地震反应研究[J]. 中国公路学报,2002(3):44-50.

[6] 牛俊武. 桥跨结构设计参数对高墩连续刚构桥抗震性能影响分析[D]. 西安:长安大学硕士学位论文,2004.

[7] 李 茜,王克海,韦 韩. 高墩梁桥地震响应分析[J]. 地震工程与工程振动,2006(3):74-76.

[8] 陈敏海. 钢管混凝土高墩大跨连续刚构桥地震响应分析[D]. 长沙:长沙理工大学硕士学位论文,2010.

[9] 侯鹏飞. 高墩大跨度连续刚构桥梁结构抗震性能研究[D]. 长沙:中南大学硕士学位论文,2010.

[10]付春辉. 预应力混凝土连续梁桥抗震性能研究[J]. 北方交通,2012(3):66-68.

[11]T．Miki，J．Niwa．Nonlinear Analysis of Reinforced Concrete Viaducts Subjected to Seismic Loads Using 3D Lattice Model[C]．First International Conference on Urban Earthquake Engineering, 2004: 433-440．

[12]Sung J, Kim, Holub C, et al. Analytical and Experimental Investigations of the Effect of Vertical Ground Motion on Rc Bridge Piers[J]. Km World, 2007(January).

[13]Guirguis J E B, Mehanny S S F. Evaluating Code Criteria for Regular Seismic Behavior of Continuous Concrete Box Girder Bridges with Unequal Height Piers[J]. Journal of Bridge Engineering, 2013, 18(6):486-498.

[14]范立础.桥梁抗震[M].上海：同济大学出版社,1997.

[15]JTG D63-2007,公路桥涵地基与基础设计规范[S].北京:人民交通出版社,2007.

[16]邵旭东,顾安邦.桥梁工程[M].北京：人民交通出版社,2007.

[17]JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2004.

[18]JTG/T B02-01-2008,公路桥梁抗震设计细则[S].北京:人民交通出版社,2008.

[19]雷俊卿,宋力勋. 汶川百花大桥震害分析与抗震性能研究[J]. 北京交通大学学报,2012(1):1-5+11.

Seismic Behavior Analysis of Continuous Rigid Frame Bridge with Pile-soil Interaction

HU Di，CHEN Rui-lin，ZHANG Chao，XIA Xiang-zhong，DENG Xiao-bo

(School of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China)

For the research of long-span continuous rigid frame bridge static and dynamic characteristics and seismic behavior, taking a (65 + 110 + 65) m prestressed concrete continuous rigid frame bridge as the engineering background, the paper adopts the finite element analysis model of the whole bridge by MIDAS Civil to calculate hear force, bending moment and stress of characterteristics of girder cross section which are under different load. And then, combining with the response spectrum method and time history analysis method for seismic response analysis, evaluation on seismic performance of the bridge is done. The results indicate that the main factors are structure internal force of gravity and prestressed effect caused by internal forces at a time. Each main girder section stress can meet the specification requirements. The first order vibration mode of main girder longitudinal drift and pier longitudinal vibrating show that the stiffness of ele vated is weaker than cross the bridge; comparing finished stage and the longest cantilever stage piers key location of the earthquake, structural seismic performance should be considered of seismic action in a different direction ; under the action of the earthquake, the bridge meets the design specification requirements, the strength and deformation structure dynamic characteristics and seismic behavior is good.

continuous rigid frame bridge；pile-soil interaction；dynamic characteristics；response spectrum method；time history analysis method；seismic behavior

2017-01

教育部高等学校博士学科点专项科研基金(20104301120004)；教育部科学技术重点项目(211127)；湖南省教育厅优秀青年项目(10B105)；第49批中国博士后科学研究基金(20110491260)；湖南省优秀博士论文奖励专项基金(YB2011B031).

胡 迪(1990-)，男，硕士研究生. 研究方向：道路与桥梁工程.

陈锐林(1971-)，男，副教授. 研究方向：桥梁结构设计理论和车桥耦合振动、风车桥系统动力学及其应用.

U445.34

A

1671-119X(2017)02-0077-07