政府补贴下企业采用电动汽车配送的时机与价格分析

高咏玲

一、引言

城市配送是城市社会经济运行的基础保障,关系着城市生产的效率与生活质量。当前,采用燃油汽车配送的成本居高不下,受城市限行和通行秩序整治的影响,其便利性受到严峻的挑战,带给城市能源和环境的压力与日俱增。因此,采用新能源汽车尤其是电动汽车配送受到广泛的关注。2014年7月,国务院印发 《关于加快新能源汽车推广应用的指导意见》(国办发 [2014]35号)。[1]2015年 3月, 交通运输部推出 《关于加快推进新能源汽车在交通运输行业推广应用的实施意见》,其中明确提出:“到2020年,新能源出租汽车和城市物流配送车辆共达到10万辆。争取当地人民政府支持,对新能源汽车不限行、不限购”。[2]在此背景下,研究如何加快电动汽车在城市配送领域的推广应用,对缓解环境和能源的压力、促进汽车产业和交通运输行业的转型升级具有重要的积极意义。

如今的商业环境中,没有什么能比新技术的发展和影响更加难以预测。[3]采用电动汽车配送的决策受成本、技术和财务激励等多重因素的影响,面临着较大的不确定性。[4]这使得不少企业选择等待和观望。然而,采用观望策略对于配送企业不一定有利。现实中,不乏企业率先采用电动汽车承担配送业务。例如:2014年,北汽新能源公司和京东商城签署战略合作协议,在两年内向京东商城提供5 000辆纯电动物流车。[5]2016年,中外运敦豪国际航空快件有限公司首批35辆纯电动物流服务车在深圳正式投入使用。该公司将和比亚迪股份有限公司合作打造基于电动汽车的物流解决方案,促进节能减排目标的实现。[6]

实物期权理论为解释和预测不确定环境下企业为何会选择推迟或尽早投资提供有效的工具。Agliardi和Sereno(2011)[7]假设污染的社会成本不确定,利用实物期权研究了政府推出碳排放税和碳限额政策的最优时机。Lukas和Welling(2014)[8]假设碳排放价格不确定,利用实物期权和博弈论研究了供应链中企业碳减排投资的最优时机。在这一环境下,丁志刚和徐琪 (2015)[9]考虑了碳减排率对低碳技术投资额和产品价格的影响,得出供应链低碳技术投资的最优时机。Fouilloux等 (2014)[10]研究了碳排放价格的风险和其他不确定因素影响下碳减排项目的最优投资时机。这些文献侧重于分析政策规制下低碳技术的投资时机。目前,各国政府纷纷推出电动汽车补贴政策[11],这一政策对投资时机的激励作用却没有得到足够的关注。在成本不确定的环境下,Kleindorfer等[12]、 Neboian 和 Spinler(2015)[13]建立了运用电动汽车更新配送车队的实物期权模型,其中,前者针对不能提前终止车辆租赁合同的情形,后者考虑了违反车辆租赁合同的选择权。此外,Yao等 (2010)[14]、Moon 等 (2011)[15]、 Banerjee 等 (2014)[16]、 Zheng等 (2015)[17]利用实物期权和纳什合作博弈研究了供应链环境下执行合同的最优时机和价格协商问题。现实中,消费者的需求对产品或服务的碳排放水平越来越敏感已成为共识。[18－19]而前述的实物期权文献较少涉及绿色敏感型需求对投资时机的影响。

在非实物期权的框架下,朱庆华和窦一杰(2011)[20]运用三阶段博弈模型分析了政府的补贴系数、产品的绿色度和定价决策。Huang等 (2013)[21]、Luo 等 (2014)[22]、 罗春林 (2014)[11]分析了政府补贴背景下电动汽车的批发价、期望销量和社会福利等。Cohen等 (2015)[23]研究了需求不确定环境下电动汽车制造商的定价、产量和政府对消费者的补贴。Ghosh和Shah(2015)[18]假设需求是关于产品绿色度的线性函数,研究了制造商的绿色度和批发价决策以及零售商的销售价格决策。Nouira等 (2016)[19]研究了绿色敏感型需求下设施选址、供应商选择和交通方式选择等问题。这些研究为分析政府补贴和绿色敏感型需求影响下供应链的定价决策提供了重要框架,但未涉及最优投资时机的选择问题。

总体而言,以往文献分别考虑了政策规制下低碳技术的投资时机[7－9]、利用电动汽车更新车队的时机[12－13]、 不确定环境下时机和定价的决策[14－17]、 政府补贴或绿色敏感型需求下绿色供应链的定价决策[11][18][20－23], 鲜有兼顾政府补贴和绿色敏感型需求的投资时机和定价的成果。鉴于此,本文采用电动汽车的使用率来反映配送服务的绿色度,在绿色敏感型需求和政府补贴的环境下,利用实物期权建立了企业采用电动汽车配送的时机、采用时机和价格的联合决策、采用时机选择和价格协商三个模型,得出采用时机和配送服务价格的解析解,揭示了电动汽车的使用率和成本的风险对决策的影响。此外,本文还分析了政府应如何提供补贴以激励企业尽早投资的问题,为企业采用电动汽车配送的决策以及政府评估政策的激励效果提供理论支持。

二、问题描述与模型假设

本文分析由一个配送企业和一个客户组成的供应链。该配送企业属于第三方物流服务供应商,将权衡采用电动汽车配送带来的影响,选择电动汽车的采用时机和相应的价格调整方案。

本文用q来表示客户的需求；θ为电动汽车在配送服务中的使用率,以下简称 “电动汽车的使用率”。θ为参数,反映配送服务的绿色度,0＜θ≤1。由此,企业基于电动汽车和燃油汽车的配送量分别为θq和(1－θ)q。近年来,为应对城市交通拥堵以及缓解交通排放污染,限制燃油货运车的通行路段和通行时间已成为我国大中城市普遍采用的交通需求管理措施。采用电动汽车配送获得的通行便利和消费者环保意识的增强将使得客户的需求对配送的绿色度敏感。与Ghosh和 Shah(2015)[18]类似,假设客户的需求q对配送服务的定价和电动汽车的使用率敏感,客户的需求q表示为

式中,a表示不考虑价格和电动汽车使用率影响下客户的需求总量,b＞0表示客户的需求对配送价格的敏感度[24],α＞0表示客户对电动汽车使用率的敏感度,p为配送服务的单位价格。

电动汽车通常分为纯电动汽车、混合动力电动汽车和燃料电池电动汽车。[4]考虑到纯电动汽车的续航里程较短、充电设施网络不够完善、充电时间较长且大多数企业缺乏管理经验,本文主要研究纯电动汽车,假设企业购买此类汽车,用于配送的单位成本c(t)不确定。利用几何布朗运动刻画c(t)的演化如下:

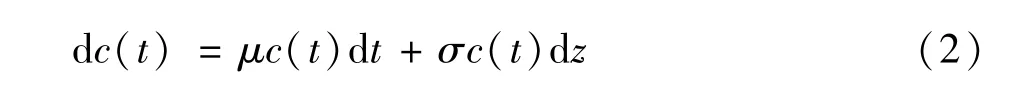
式中,μ和σ分别为采用电动汽车配送的成本的预期增长率和波动率,t≥0。

采用电动汽车或燃油汽车配送的单位成本包括购置车辆的折旧费用、维护费用、人员工资、能源费用和管理费用等。假设基于燃油汽车配送的单位成本cF为固定值。采用电动汽车配送后,配送企业将获得政府补贴sθq,其中s为单位补贴。当需求q的单位为吨、公里或吨公里时,s表示运营补贴；当需求q表示车辆数时,s表示购置补贴。

城市配送包括城市工业配送、城市商业配送和城市快件配送三种类型。本文采用以下三种模型分析电动汽车的采用决策。

第一,单阶段采用时机决策模型。该模型假定配送价格外生,由配送企业选择采用电动汽车配送的时机 (以下简称为 “采用时机”),针对部分快递企业和货运企业因竞争激烈和行业集中度低而提价困难的情形。

第二,单阶段采用时机与价格决策模型。此模型中,配送企业对采用时机与价格进行联合决策,针对配送企业依靠垄断地位来调价的情形。

第三,两阶段采用时机选择与价格协商模型。该模型中,在第一阶段,配送企业首先与客户协商配送服务的价格；在第二阶段,配送企业根据这一价格来选择最优的采用时机。此模型针对配送企业与客户的议价能力的差距不太悬殊的情形。

这三种情形下的决策结果和参数分别以下标i＝0,1,2表示,如配送服务的价格为pi,采用时机为ci,客户的需求为qi。假设这三种情形下配送企业和客户的效用大于0,客户的需求大于0,即qi＝abpi＋αθ＞0。本文研究配送企业如何选择最优的采用时机和配送服务的价格,还分析了政府应如何提供补贴si,以激励企业在t＝0时采用电动汽车配送。

三、企业采用电动汽车配送的时机和定价的实物期权模型

（一）单阶段采用时机决策

单阶段的采用时机决策模型中,配送服务的价格p0为固定值,配送企业的决策变量为采用时机。t时刻企业采用电动汽车配送的净现值φ(t)为:

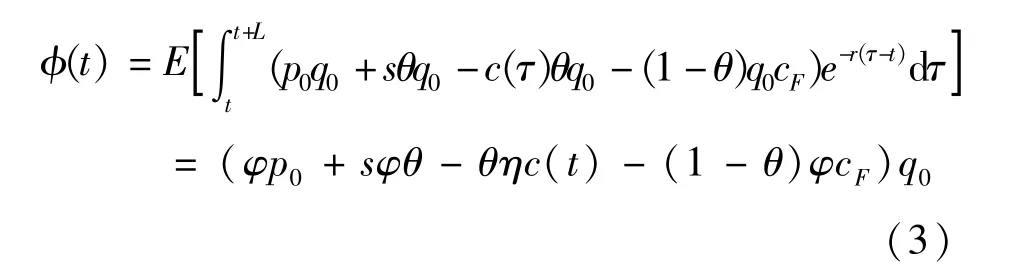
式中,客户的需求q0＝a－bp0＋αθ,L为合同期,,乘数φ和η分别表示参数和不确定因素c(t)的期初值和合同期内期望值之间的关系。

令x(t)＝θηq0c(t)。由于θ、η和q0为固定值,x(t)服从预期增长率为μ和波动率为σ的几何布朗运动。在成本不确定的环境下,配送企业可以选择等等看,获得等待的灵活性价值,其延期期权的价值可表示为F(x(t))＝φ(t)＋＝max｛φ(t),0｝。考虑到时间间隔dt内,企业的投资机会的预期总回报等于其资本的预期增值率[25],即rFdt＝E(dF)。式中:F为F(x(t))的简写；可知期权价值F满足微分方程将F＝ρxβ代入此微分方程,可得β为方程的根。期权价值F应满足边界条件、价值匹配和平滑粘贴条件为[15][25]:根据边界条件可知,期权价值参数

根据价值匹配和平滑粘贴条件,可得价格外生下配送企业采用电动汽车配送的期权价值F为:

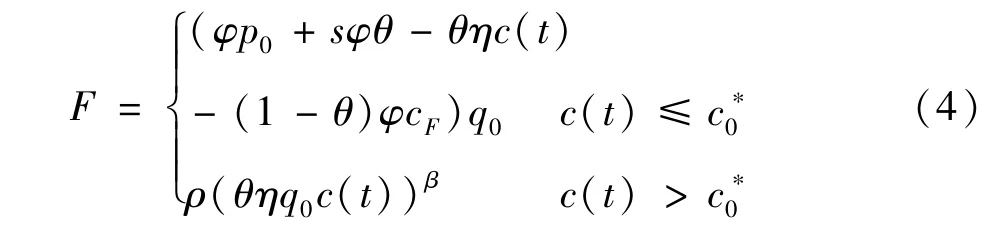
式中,采用时机的成本的临界值

由式 (4)可知,配送企业通过比较成本临界值和t时刻的成本c(t)来选择观望还是采用电动汽车配送。t＝0时,若成本c(0)大于,配送企业将选择继续等待,获得等待的灵活性价值；当c(0)小于或等于时,配送企业才采用电动汽车配送。成本临界值中期权价值参数β反映了成本的风险σ和成本的增长率μ的影响。

成本的临界值是政府补贴的增函数。若政府提高补贴s,成本临界值也随之提高。利用可得,若t＝0为企业采用电动汽车配送的最优时机,政府补贴s应大于或等于s0:

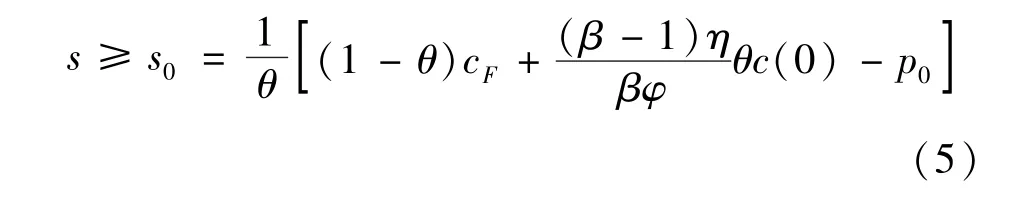
单阶段采用时机决策情形下政府的最低补贴额s0反映了政府对t＝0时采用电动汽车配送所提供的补偿。该补贴s0是燃油汽车配送的单位成本cF和电动汽车配送的单位成本c(0)的增函数,是配送服务价格p0的减函数,是电动汽车使用率θ的分式函数。

（二）单阶段采用时机与价格的联合决策

本节考虑配送企业根据自身利益的最大化来选择采用时机c1和服务定价p1的情形。这一情形下配送企业的价值π1t()为:

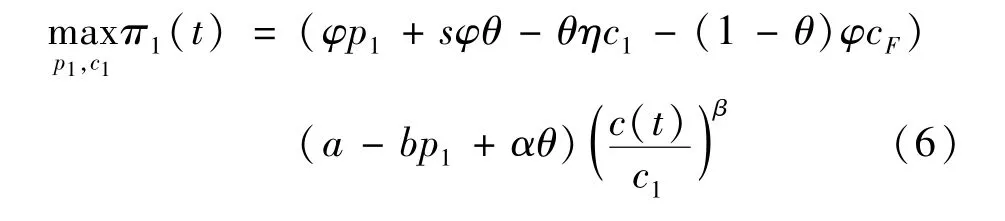
式 (6)中(c(t)/c1)β为折现因子。式 (6)是一个含二维变量的无约束的非线性优化问题。为简化表述令N＝sθ－(1－θ)cF,M＝a＋αθ＞0。 为了使问题有意义,假设对π1(t)求解关于p1和c1的一阶导数可得,单阶段采用时机与价格联合决策情形下最优定价和采用时机的成本临界值为:

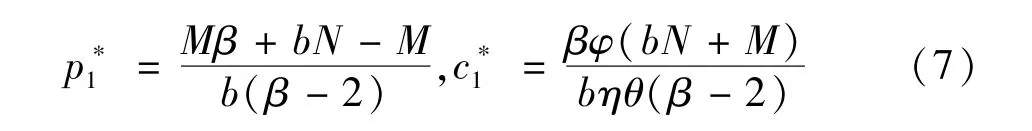
在驻点,故驻点处海塞矩阵为负定,为此问题的最优解。

政府补贴作为促进新能源汽车推广与应用的重要政策工具,近年来被各级政府普遍采用。若政府通过提供补贴使得企业在t＝0时刻采用电动汽车配送,即,可得单阶段采用时机和价格联合决策情形下政府的补贴应满足:

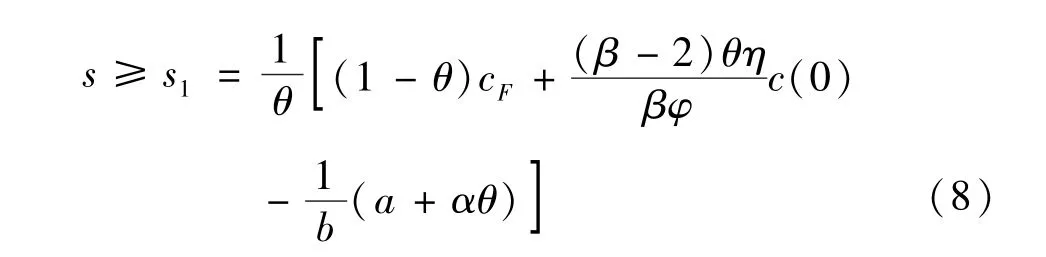
式 (8)中,政府的最低补贴额s1随着电动汽车配送的成本c(0)和燃油汽车配送的成本cF的增加而增加。与s0类似,政府的最低补贴额s1也是电动汽车使用率θ的分式函数。与s0不同,s1反映了客户的需求对配送价格的敏感度b和电动汽车使用率的敏感度α的影响。客户的需求对电动汽车的使用率越敏感,政府的最低补贴额s1越低。

（三）两阶段采用时机选择与价格协商

为反映决策者的定价权威对投资时机和定价结果的影响,可将实物期权和纳什讨价还价博弈相结合展开研究。[14－17]本文将绿色敏感型需求和政府补贴引入实物期权和纳什讨价还价博弈模型中,考虑配送企业先与客户协商配送服务的价格p2,然后再择机实施电动汽车使用率为θ的配送服务。

采用逆向归纳法,第二阶段配送企业通过选择最优的采用时机来最大化其价值π2(t):

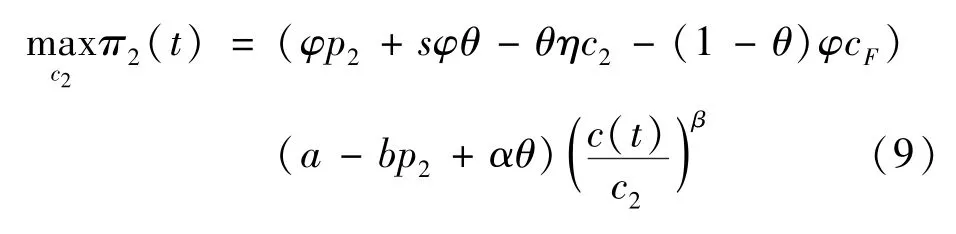
根据一阶最优条件,可得两阶段采用时机选择与价格协商情形下采用时机的成本临界值为:

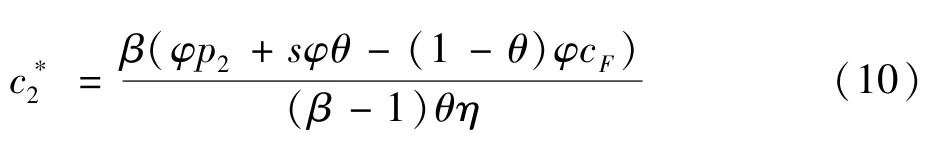
π2(t)反映t时刻配送企业签订服务供应合同的价值。客户与该配送企业签订合同的价值为:式中,R为客户销售配送服务的价格,客户的需求q2＝a－bp2＋αθ。假设配送企业的保留效用为VLSP＝0,客户的保留效用VC＝,X表示客户采用其他供应商配送的单价。假设配送企业和客户在纳什合作博弈的框架下议价,所得的价格能使得双方获得的效用增加值之乘积为最大,这一乘积为(π2(t)－VLSP)γ(UCVC)1－γ。因此,第一阶段,配送企业和客户协商配送服务价格p2如下:

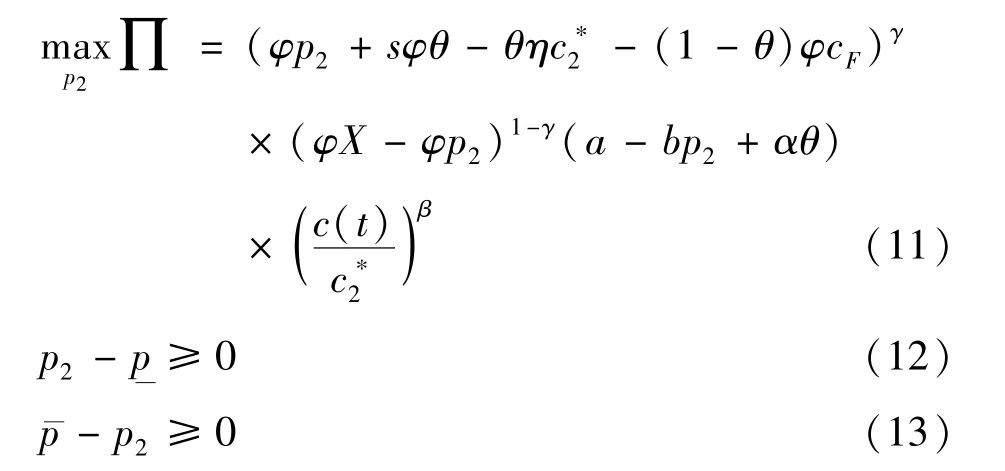
式中,配送企业的定价权威为γ,γ∈(0,1)。用代表配送服务价格的上下限,均小于客户采用其他供应商配送的单价X,保证双方的效用非负。

上述问题是一个含一维变量的有约束的非线性优化问题,利用库恩塔克条件[26],可得两阶段采用时机选择与价格协商模型中配送服务的价格(求解过程见附录):

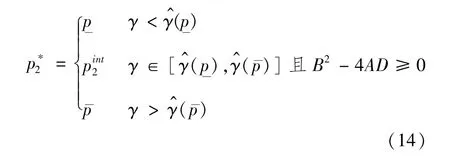
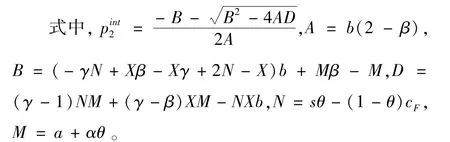
由此可知,若配送企业将选择等待；当时,配送企业将选择采用电动汽车配送。由于与政府补贴s有关,政府可通过调整补贴s使得c(0),以满足t＝0是企业采用电动汽车配送的最优时机。因此,两阶段采用时机选择与价格协商的情形下,政府的最低补贴额s2满足如下方程:

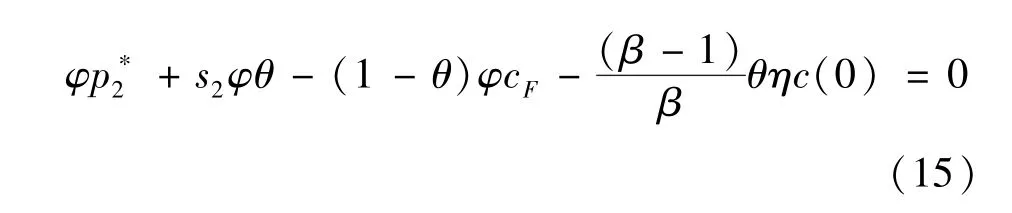
由式 (15)可知,两阶段情形下政府的最低补贴额s2是电动汽车的使用率θ、期权价值参数β和配送企业定价权威γ的非线性函数。

四、电动汽车的使用率和成本的波动率对决策的影响

本节中,命题1至命题6分析了电动汽车的使用率和成本的波动率对单阶段模型的求解结果的影响。然后,本文运用数值分析观察了这两个因素对两阶段采用时机选择与价格协商结果的影响。

根据期权价值参数β＜0、配送价格p0大于燃油汽车配送的成本cF和需求大于0,可知,得到命题1。

命题1：配送企业采用时机的成本临界值和

命题1表明,电动汽车的使用率θ越高,配送企业采用电动汽车配送的成本临界值均随着电动汽车的使用率θ的提高而降低,即越低,采用电动汽车配送的时机越晚。这是因为电动汽车的使用率越高,对配送企业的成本和需求的影响更大,配送企业会更谨慎地选择采用时机,要求采用电动汽车配送的成本更低,才实施基于电动汽车的配送。

命题2：政府的最低补贴额s0和s1是电动汽车的使用率θ的增函数,即

无论配送企业是否调整配送服务的价格,政府的最低补贴额s0和s1均随着电动汽车的使用率的提高而提高,如命题2所述。其原因在于:电动汽车使用率更高的配送企业,其采用时机的成本临界值(或)更低,因而需要政府提供更多补贴,以满足t＝0是配送企业的最优采用时机。

对单阶段时机与价格联合决策的定价结果求解关于电动汽车的使用率θ的导数,可得由此可得命题3。

命题3：当政府补贴s小于时,随着电动汽车使用率θ的提高,单阶段模型中配送服务定价随之增加；当政府补贴大于时,则相反,即当时,, 当时,, 式中

命题3表明,若政府补贴较低,电动汽车的使用率θ越高,配送服务的定价也越高。这说明,当政府补贴较低时,企业因配送服务的绿色度的提升而提价。若政府补贴较高,则相反。存在政府补贴临界值决定着单阶段模型中配送服务的定价与电动汽车使用率θ之间的关系。由期权价值参数可知,政府补贴的阙值由成本的增长率、成本的波动率、燃油汽车配送的成本、需求对价格和电动汽车使用率的敏感程度决定。基于电动汽车配送的成本的增长率和成本的波动率影响着与θ之间的关系。

根据,易证决策变量关于σ的导数,由此可得命题4至命题6。

命题4：配送企业的成本临界值随着成本波动率σ的提高而降低,即

命题4表明,随着成本波动率σ的提高,成本临界值随之降低,配送企业的投资时机呈现出推迟的趋势。与传统的燃油车配送不同,大多数企业缺乏基于电动汽车配送的管理经验。在电池的使用寿命、续航里程、充电设施网络和充电时间等因素的影响下,采用电动汽车配送的成本的风险越大,配送企业越倾向于等待和观望,越重视等待所带来的灵活性价值,直至达到更低的成本临界值才投资。

命题5：政府的最低补贴额s0或s1随着成本波动率σ的提高而提高,即。

采用燃油车配送会造成空气污染和噪音污染等外部成本,难以在市场体系中恰当地反映。若企业未能获得采用电动汽车配送的全部利益,会导致其使用不足。因此,政府补贴是推动环保技术在经济上可行的常见政策工具。命题5揭示了政府的最低补贴额(s0或s1)与成本波动率σ之间的关系。成本波动率越高,政府的最低补贴额 (s0或s1)也越高。这是因为成本波动率σ的提高将导致成本的临界值的下降,此时政府需增加补贴,使配送企业的最优采用时机为t＝0。

命题6：单阶段模型中配送服务的定价随着成本波动率σ的提高而降低,即

由命题6可知,成本波动率σ的增加将导致配送服务的价格的下降。这是因为单阶段模型中配送服务的价格和成本的临界值由联合决策所决定,考虑到成本临界值随着成本波动率σ的提高而降低,配送服务的价格也随之下降。

两阶段采用时机选择与价格协商模型中,配送服务的价格与电动汽车的使用率θ之间存在非单调的关系,如图1.a所示。在其他参数相同的条件下,当μ＝0.05时随θ的增加而提高,当μ＝0.048时随θ的增加而下降,图1.b中均随着θ的增加而下降。这说明,与单阶段分析的结果类似,电动汽车的使用率θ和两阶段模型的定价结果之间的关系也受成本的增长率μ的影响。本文中以下参数的取值相同:r＝0.08,L＝10,a＝100,b＝5,随着θ的增加,企业的成本临界值更低,越倾向于推迟投资,此时政府需提高其最低补贴额s2,以激励企业尽早投资,如图1.c和1.d所示。

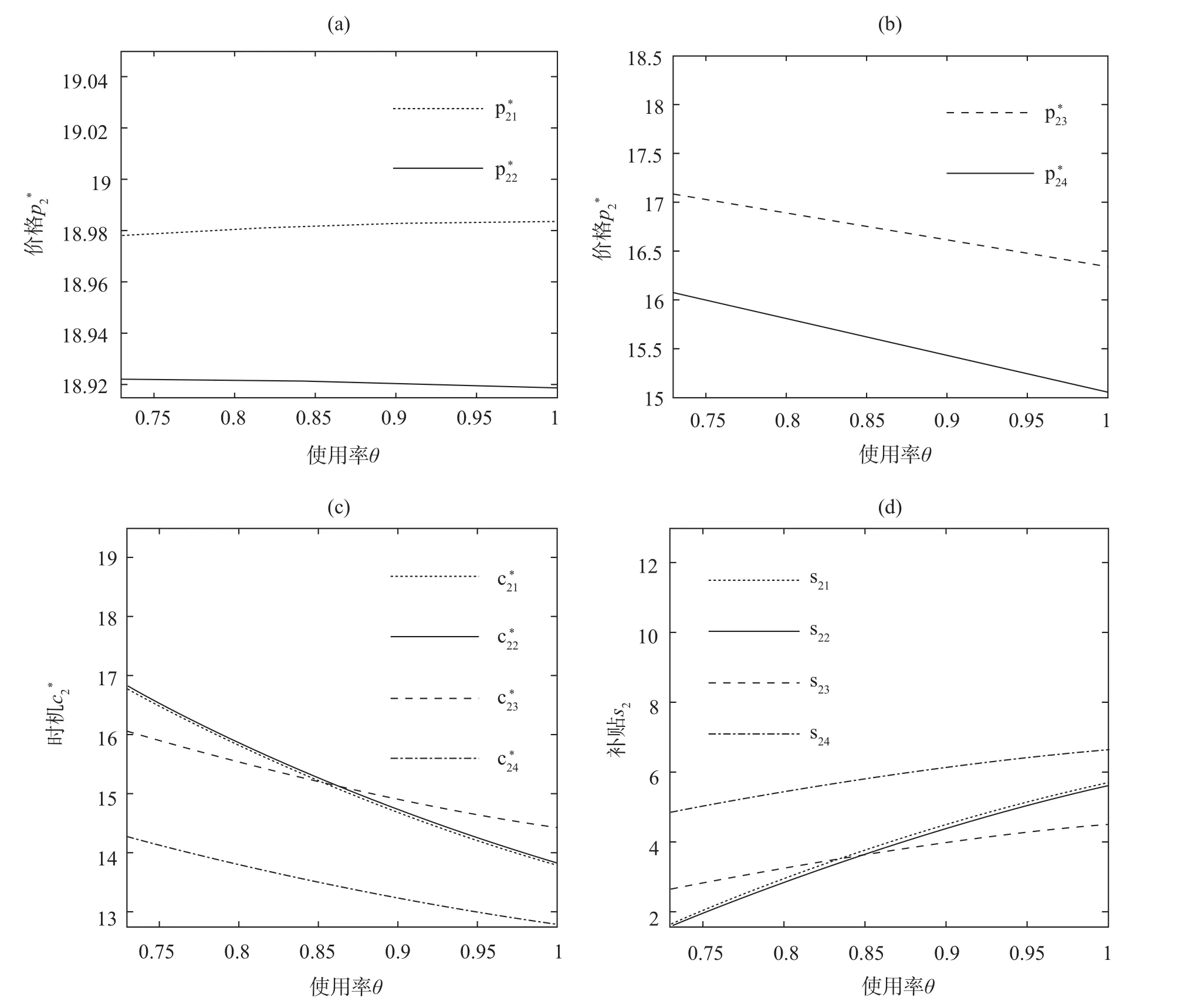
图1 电动汽车的使用率对两阶段模型的决策变量的影响

与单阶段分析中成本波动率的影响类似,两阶段模型中配送服务的价格和配送企业的成本临界值均随成本的波动率σ的增加而降低,如图2.a和2.b所示。这揭示了成本风险的增加使得配送企业更倾向于推迟投资,要求基于电动汽车配送的成本更低,配送服务的价格也因而更低。此时,政府需要加大补贴力度以激励企业尽早投资,如图2.c所示。

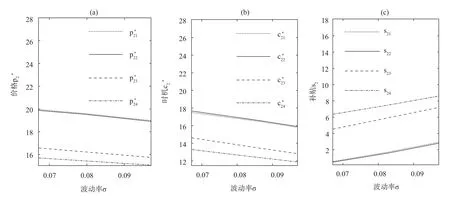
图2 成本波动率对两阶段模型的决策变量的影响

通过上述分析可知,在配送企业不调整价格、调整价格或与客户协商价格三种情形下,不确定性和电动汽车使用率的变化对采用时机和政府的最低补贴额的影响类似,对配送价格的影响不同。具体而言,成本的风险越大或电动汽车使用率的提高均促使企业通过等待获得灵活性的价值,直至采用电动汽车配送的成本更低才投资。政府的最低补贴额也随着成本的风险或电动汽车使用率的增加而提高。成本的增长率影响配送企业如何根据电动汽车的使用率来调整配送服务的价格,但不影响成本波动率和配送服务价格之间的关系。

五、结论

在成本不确定和绿色敏感型需求的环境下,笔者运用实物期权和纳什合作博弈研究了政府补贴背景下企业应何时采用电动汽车配送以及如何调整配送服务价格的问题,建立了采用时机选择、采用时机和价格联合决策、采用时机选择和价格协商三个模型,推导出配送企业的采用时机和服务价格的解析解。此外,本文还提出了针对配送企业采用时机的政府的最低补贴额,以激励企业尽早投资。

本文揭示了成本的风险和电动汽车的使用率对决策的影响,发现这两个因素的变化对采用时机和政府最低补贴额的影响类似,但对配送服务价格的影响不同。具体而言,随着成本风险的增加或电动汽车使用率的提高,配送企业的成本临界值更低,越倾向于推迟投资。这促使政府提高最低补贴额。成本波动率的提高将导致成本临界值的下降,配送企业因而下调配送服务的价格。与这一单调关系不同,配送服务的价格与电动汽车的使用率之间存在非单调的关系,受成本增长率的影响。上述结论不仅补充了经典的风险与投资决策之间的关系的结论,还反映出以电动汽车的使用率为代表的投资特性对配送企业决策的影响,以丰富和拓展已有的研究。

本文的研究结果对加速推广电动汽车在配送领域的应用以及配送企业的决策有一定的启示意义。

首先,降低成本的风险有助于推动企业尽早采用电动汽车配送。现实中,新能源汽车在配送领域的应用尚未成熟。政府可通过增加充电设施数量、建立智能充换电服务网络和组织培训等方式提升企业控制成本风险的能力[27],为电动汽车在物流领域的应用提供便利条件。

其次,为推动企业尽早采用电动汽车配送,有必要建立差别化补贴的动态调整机制,考虑电动汽车的使用率、消费者对配送绿色度的敏感程度和基于电动汽车和燃油汽车配送的成本对补贴的影响。

最后,在城市交通需求管理日益严格和消费者的环保意识日益增强的环境下,基于电动汽车配送为企业未来的发展提供了不容忽视的价值。配送企业在分析电动汽车的使用率对成本的影响的同时,也要重视它对需求的影响,引导和鼓励消费者选择基于电动汽车的配送服务。

尽管几何布朗运动常被用来描述运营成本的不确定性[14－15][17], 但它在电动汽车采用决策问题中的普适性需后续研究进一步验证。本文假设企业基于燃油汽车配送的成本为固定值,得出企业购买电动汽车用于配送的时机和定价的解析解。后续研究可以放松这一假设,在成本和需求多重不确定的环境下分析企业租赁电动汽车用于配送的时机和定价等决策。此外,本文假设决策者是理性的,下一步研究可考虑决策者在不确定环境下的有限理性对投资决策的影响。

附录

令V＝lnΠ,以V为目标函数构造拉格朗日函数L2可得,

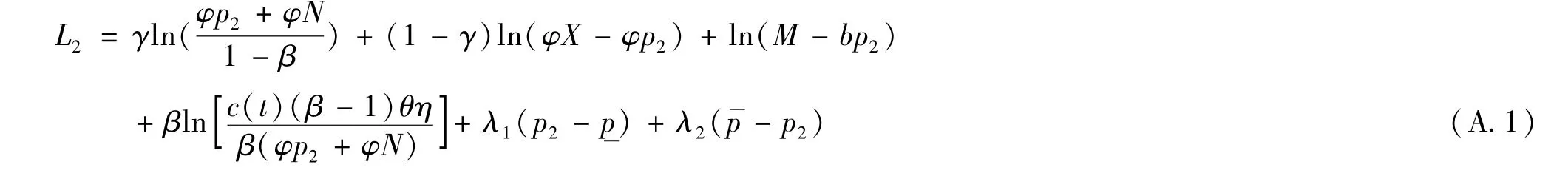
该问题的库恩塔克条件满足[26]:

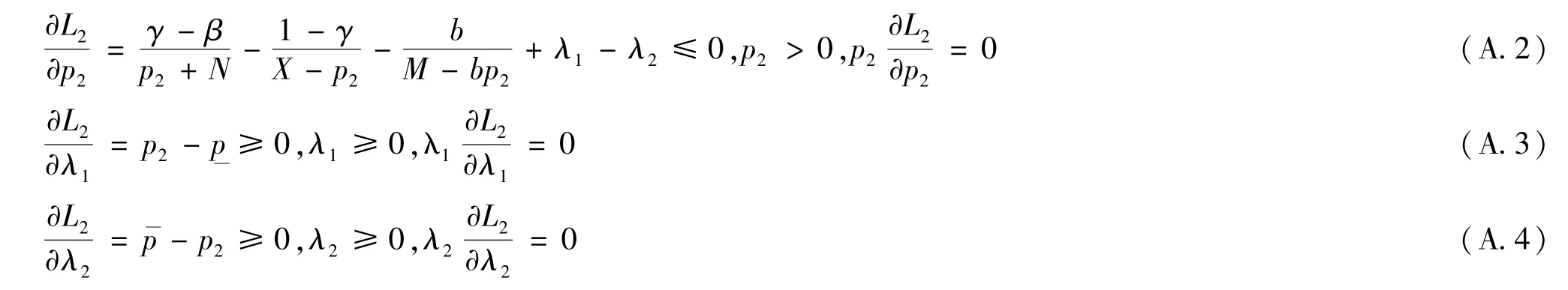
若λ1＞0和λ2＝0可得。令由式 (A.1)得出,λ1＞0等价于。若λ1＝0和λ2＞0可得。代入式 (A.2),λ2＞0等价于。若λ1＞0且λ2＞0,最优解不存在。当λ1＝λ2＝0时,驻点服从,式中A、B、D在文中式 (14)中定义。为保证问题的经济含义,假设客户采用其他供应商配送的单价,其中, 以保证使得大于X,驻点不可行。假设且V在连续。由可得,驻点属于区间时,该点为极大值点。由此可得式 (14)。

[1]国务院办公厅.国务院办公厅关于加快新能源汽车推广应用的指导意见:国办发 〔2014〕35号[A/OL].(2014－07－21)[2016－12－05].http://www.gov.cn/zhengce/content/2014 －07/21/content＿ 8936.htm.

[2]交通运输部.交通运输部关于加快推进新能源汽车在交通运输行业推广应用的实施意见[EB/OL].(2015－03－18)[2016－12－05].http://www.moc.gov.cn/zfxxgk/bnssj/dlyss/201503/t20150318＿1790182.html.

[3]Reeves M,Levin S,Ueda D.The Biology of Corporate Survival[J].Harvard Business Review,2016,January-February:46 －55.

[4]Pelletier S,Jabali O,Laporte G.Goods Distribution with Electric Vehicles:Review and Research Perspectives[J].Transportation Science,2016,50(1):3－22.

[5]吴影.新秀崛起纯电动物流车前景可期[N].中国工业报,2015－04－17.

[6]汪名立.中外运敦豪批量应用纯电动物流车[N].国际商报,2016－01－07.

[7]Agliardi E,Sereno L.The Effects of Environmental Taxes and Quotas on the Optimal Timing of Emission Reductions under Choquet-brownian Uncertainty[J].Economic Modelling,2011,28(6):2793 －2802.

[8]Lukas E,Welling A.Timing and Eco(nomic)Efficiency of Climate-friendly Investments in Supply Chains[J].European Journal of Operational Research,2014,233(2):448－457.

[9]丁志刚,徐琪.碳限额与交易政策下供应链低碳技术投资时机研究[J].北京理工大学学报 (社会科学版),2015,17(5):9－14.

[10]Fouilloux J,Moraux F,Viviani J L.Investing in Finite-life Carbon Emissions Reduction Program under Risk and Idiosyncratic Uncertainty[J].Energy Policy,2014,82:310－320.

[11]罗春林.基于政府补贴的电动汽车供应链策略研究[J].管理评论,2014,26(12):198－205.

[12]Kleindorfer P R,Neboian A,Roset A,et al.Fleet Renewal with Electric Vehicles at La Poste[J].Interfaces,2012,42(5):465 －477.

[13]Neboian A,Spinler S.Fleet Replacement,Technology Choice,and the Option To Breach a Leasing Contract[J].Decision Sciences,2015,46(1):7－35.

[14]Yao T,Jiang B,Young S T,et al.Outsourcing Timing,Contract Selection,and Negotiation [J].International Journal of Production Research,2010,48(2):305－326.

[15]Moon Y M,Yao T,Park S.Price Negotiation under Uncertainty[J].International Journal of Production Economics,2011,134(2):413 －423.

[16]Banerjee S,Güçbilmez U,Pawlina G.Optimal Exercise of Jointly Held Real Options:A Nash Bargaining Approach with Value Diversion [J].European Journal of Operational Research,2014,239(2):565－578.

[17]Zheng S,Negenborn R R.Price Negotiation between Supplier and Buyer under Uncertainty with Fixed Demand and Elastic Demand [J].International Journal of Production Economics,2015,167:35－44.

[18]Ghosh D,Shah J.Supply Chain Analysis under Green Sensitive Consumer Demand and Cost Sharing Contract[J].International Journal of Production Economics,2015,164:319－329.

[19]Nouira I,Hammami R,Frein Y,et al.Design of Forward Supply Chains:Impact of a Carbon Emissions-sensitive Demand [J].International Journal of Production Economics,2016,173:80－98.

[20]朱庆华,窦一杰.基于政府补贴分析的绿色供应链管理博弈模型[J].管理科学学报,2011,14(6):86－95.

[21]Huang J,Leng M,Liang L,Liu J.Promoting Electric Automobiles:Supply Chain Analysis under a Government's Subsidy Incentive Scheme[J].IIE Transactions,2013,45(8):826－844.

[22]Luo C,Leng M,Huang J,Liang L.Supply Chain Analysis under a Price-discount Incentive Scheme for Electric Vehicles[J].European Journal of Operational Research,2014,235(1):329－333.

[23]Cohen M C,Lobel R,Perakis G.The Impact of Demand Uncertainty on Consumer Subsidies for Green Technology Adoption [J].Management Science,2015,62(5):1235－1258.

[24]朱钰,程晋石,孙浩.考虑品牌效应的货运代理供应链博弈模型[J].中央财经大学学报,2016,11:123－128.

[25]Dixit A K,Pindyck R S.Investment under Uncertainty[M].Princeton:Princeton University Press,1994:140－143.

[26]Chiang A C,Wainwright K.Fundamental Methods of Mathematical Economics[M].New York:McGraw Hill,2005:404－405.

[27]Sierzchula W,Bakker S,Maat K,Wee B.The Influence of Financial Incentives and Other Socio-economic Factors on Electric Vehicle Adoption[J].Energy Policy,2014,68:183 －194.