基于联合供电的GEO卫星电推进工作策略*

陈晓杰，李 鉴，朱振华，周徐斌，沈毅力

(上海卫星工程研究所，上海 201100)



基于联合供电的GEO卫星电推进工作策略*

陈晓杰，李 鉴，朱振华，周徐斌，沈毅力

(上海卫星工程研究所，上海 201100)

针对电推进系统高功率需求，以整星能源的高效利用为目标，以电推力器的复杂工程参数和整星能源为约束，提出基于太阳电池阵和蓄电池组联合供电的静止轨道卫星电推进在轨工作策略，定量分析不同电推进类型、太阳翼构型、电源系统配置等对工作策略的影响，得到复杂工程约束条件下的南北位保、东西位保和角动量卸载控制周期的优选方法.仿真算例表明，在留有工程设计余量的情况下，根据该方法优选得到的电推进工作策略可以满足电推进系统的使用要求和整星能源平衡要求，与采用增大太阳帆板面积的方法相比，可避免卫星平台承重能力降低(约60 kg)，并提高整星能源利用率. 关键词： 电推进；联合供电；工作策略；南北位保；东西位保；角动量卸载

0 引 言

卫星平台的承载能力包括质量和功率两方面，利用电推进的高比冲特性，可提高卫星承重能力、延长在轨寿命，国内外开展的大量电推进系统应用研究[1-2]均以此为基础，尤其在通信卫星领域的应用最为广泛[3]，主要用于地球静止轨道卫星的位置保持、轨道转移[4]和姿态控制等方面.

然而，除了高比冲特性，电推进还具有高功率需求(单个电推进工作功率1.5～6 kW)，为卫星平台提升承重能力的同时，也带来了功率方面的负担，在保证卫星主业务的前提下，通常会增大太阳帆板面积以维持电推进的工作.一般通信卫星平台的功率在10 kW左右[5]，甚至更高，千瓦级的电推进功率需求可以被卫星平台所消化，但在一定程度上也造成了卫星能源的浪费，因为推力器工作时间只占卫星整个寿命期的5%～8%.

目前国内高轨遥感卫星功率一般在2～3.2 kW左右，在应用电推进的过程中面临能源短缺的难题.增大太阳电池阵面积可解决电推进能源需求，但同时也存在以下影响：需增加帆板及电池片质量，造成平台承重能力降低；部分能源长时间不能有效利用，整星能源利用率低；存在动力学耦合风险，影响卫星高精度高稳定的性能[6-8].

文献[9]以位置保持效率为指标给出了电推力器的最佳安装位置的确定方法，文献[10]研究了电推进位置保持控制及其与偏心率联合控制的方法，文献[11]研究了电推力器用于角动量卸载的算法，上述研究分别得到了高轨卫星的电推进系统在安装布局、位置保持和角动量卸载方面的应用方法或策略.

本文以整星能源的高效利用为目标，以电推进额定工作时间、额定开关机次数等关键工程参数和整星能源为约束，提出了基于太阳电池阵和蓄电池组联合供电的静止轨道卫星电推进在轨南北位保、东西位保和角动量卸载的控制周期的优选方法，并以某静止轨道遥感型号为基础开展了应用分析.

1 卫星能源与电推力器性能约束下的工作策略

1.1 联合供电时的能源平衡分析

光照期电推进工作时，采用电池阵和锂电池联合供电；地影期，卫星进地影前或者出地影后电推进开始工作，采用锂电池供电.由于电推进的功率需求高，电推力器执行任务时受卫星能源供应的限制.

当Wout-Wsat≥NWep时，Wout为太阳电池阵的输出功率、Wsat为除电推进之外的卫星功耗、N为同时工作的电推力器数量、Wep为单个电推力器工作所需功率，完全由太阳电池阵供电，电推力器的单次工作时长不受能源限制，但这种情况卫星能源利用率低.

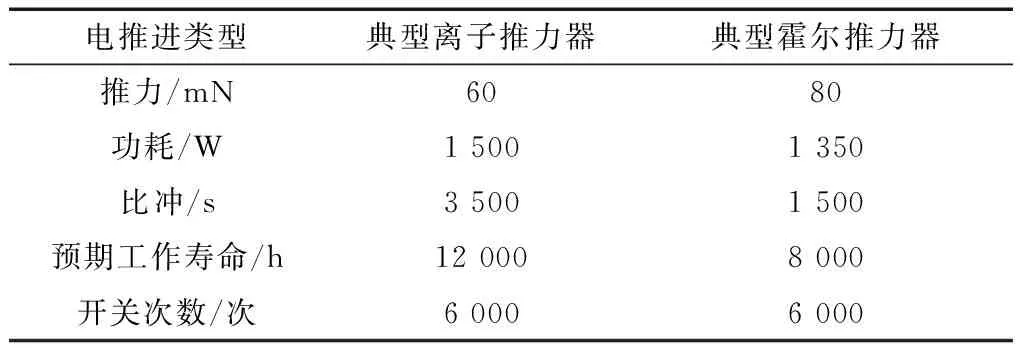
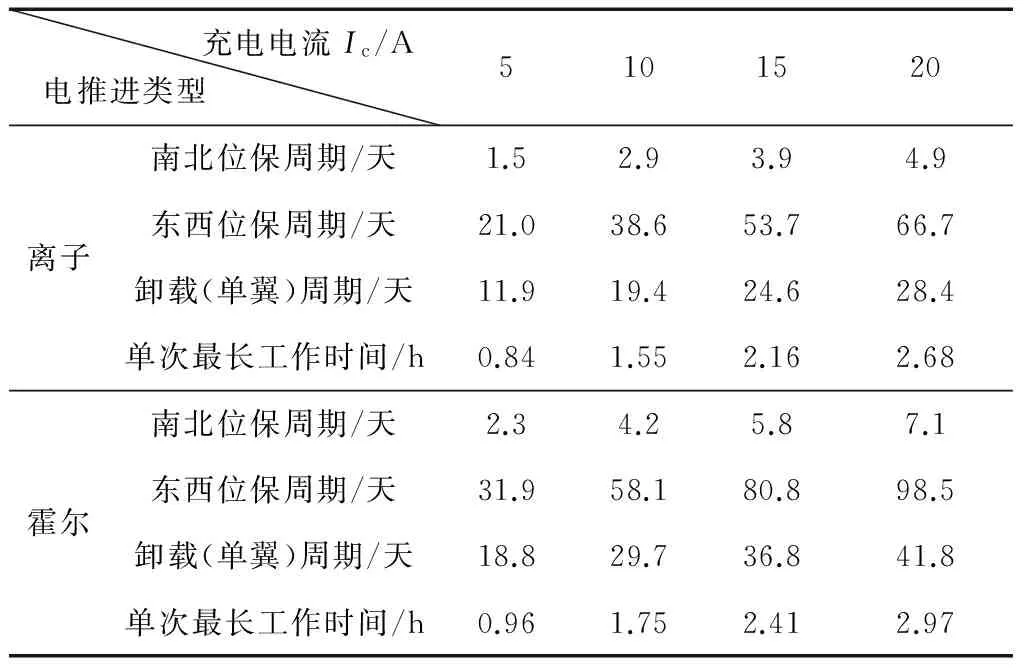
当0

(1)

式中，Dmean为额定最大放电深度.蓄电池组放电后，需要一定的充电时间，应确保卫星能源单圈平衡.采用在升交点和降交点附近[10]进行南北位保、一轨分为相隔180°的两个开机时段进行东西位保[11-12]的典型策略，且考虑存在阴影期的恶劣情况，电推进单次最长工作时间t、蓄电池组充电时间tc和最长阴影时间ts满足(单位：h)：

t+tc+ts≤12

(2)

其中充电时间

(3)

式中：Ic为恒流模式充电电流；C为恒压模式充电时间，通常为1 h左右.

最长阴影ts=72 min，则有

(4)

1.2 电推力器的工作时间分析

电推力器的工作时间分为单次工作时间和总工作时间两项.

电推力器的单次最长工作时间受卫星能源限制.当0

(5)

如图1所示，此时电推进工作所对应的放电深度和工作时长均在直线段OA上，不受蓄电池充电时间限制.

(6)

此时受蓄电池充电时间限制，电推力器工作时间不能再延长.

任何情况下，Dmax必须小于等于电池的额定放电深度Dmean.

图1 电推力器工作时间与蓄电池组放电深度关系Fig.1 Relations between working hours of electric propulsion system and discharge depth of batteries

采用在升交点和降交点附近进行南北位保、一轨分为相隔180°的两个开机时段进行东西位保的典型策略，执行南北位保、东西位保和卸载任务时，则某个电推力器需要的工作时间分别为

(7)

(8)

(9)

式中：ΔtiNSSK为第i次南北位保任务需要的电推进位保工作时间；ΔtiEWSK为第i次东西位保任务需要的电推进位保工作时间；ΔtiMU为第i次角动量卸载任务需要的电推进工作时间；mio和mif是第i次任务的始末质量；ΔviNSSK是第i次南北位保任务所需速度增量；ΔviEWSK是第i次东西位保任务所需速度增量；Δli是第i次任务的角动量增量；ηiNSSK为第i次南北位保任务的推力效率；ηiEWSK为第i次东西位保任务的推力效率；ηiMU为第i次角动量卸载任务的推力效率；di是第i次角动量卸载任务的推力至卫星质心距离.其中，在整个飞行任务期间可认为Fi、ηiNSSK、ηiEWSK、ηiMU和di始终保持不变，分别为F0、η0NSSK、η0EWSK、η0MU和d0.

则整个飞行任务期间，对于某个电推力器，其执行位保和卸载任务的总工作时间需满足：

(10)

式中：ttotal为整个任务需要的电推进工作时间；mo和mf是整个任务的始末质量；ΔvNSSK是一年南北位保任务所需速度增量；ΔvEWSK是一年东西位保任务所需速度增量；Δl是一年角动量卸载任务的角动量增量；tER为电推力器的工作寿命(性能)；R为设计冗余系数.

对于某次卫星飞行任务，mo、mf、Δv和Δl都是确定值；在选用某型电推力器后，F0随之确定.因此，电推力器的总工作时间只和η0NSSK、η0EWSK、η0MU、d0相关.

1.3 蓄电池组的放电深度分析

每次南北位保、东西位保和角动量卸载时对应的放电深度DNSSK、DEWSK、DMU须小于等于允许的最大放电深度，结合式(1)、(7)、(9)可得到：

(11)

(12)

(13)

1.4 电推力器性能约束下的控制周期分析

对于单次工作，将式(11)～(13)转换，可得控制周期与卫星能源的关系

(14)

(15)

(16)

式中：ΔvNSSK是一年内南北位保任务所需速度增量；ΔvEWSK为一年内东西位保任务所需速度增量；Δl0为一天内的角动量增量.可见，南北位保、东西位保和卸载最长周期均受卫星充电功率UIc限制，但与蓄电池组容量无关.

最恶劣情况为连续进行南北位保、东西位保和卸载，则有

DNSSK+DEWSK+DMU≤Dmax

(17)

因此，为确保电推进工作时的卫星能源平衡，除了需要Dmax满足式(11)-(13)的要求，同时还应使图1中点A的值越大越好，由式(6)可知，充电功率UIc越大、工作的电推力器数量N越多电推力器的单次工作时间可越长.

对于整个飞行任务，执行位保和卸载任务时的电推进工作时间之和不大于电推力器的额定工作时间，并留有一定冗余，则

(18)

式中tER为电推力器的额定工作时间.

同时，执行位保和卸载任务时的电推进工作次数之和不大于电推力器的额定工作次数，并留有一定冗余，则

(19)

式中：NNS为电推力器用于南北位保的开关机次数；NEW为电推力器用于东西位保的开关机次数；NMU电推力器用于动量轮卸载的开关机次数；NER为电推力器的额定开关机次数.根据开关机次数和控制周期的关系，可得

(20)

式中：TNS为电推力器用于南北位保时的控制周期(单位为天)；TEW为电推力器用于东西位保时的控制周期(单位为天)；TMU电推力器用于角动量卸载的控制周期(单位为天)；LD为卫星设计寿命(单位为年).

受电推力器性能约束，TNS、TEW和TMU必须同时满足式(18)和(20).对于双太阳翼的卫星，由于结构对称性，引起角动量漂移的法向太阳光压力矩较小，角动量积累较慢，可几周卸载一次；对于单太阳翼的卫星，由于结构不对称，法向太阳光压力矩大，角动量积累快，卸载周期的选取还需考虑姿控系统的配置和能力.

1.5 小结

重点分析卫星能源与电推力器性能约束下的电推进南北位保、东西位保和角动量卸载的控制周期算法，得到结论：同等条件下霍尔电推进对于蓄电池组的放电要求更小；增大蓄电池组容量、母线电压、充电功率、同时工作的电推力器数量可以降低电推力器工作时的蓄电池放电深度；电推力器的单次最长工作时间主要受推力器功率和卫星能源限制；电推力器的南北位保、东西位保和角动量卸载的最长控制周期受额定工作次数、额定工作时间、充电功率等的限制，须同时满足式(18)和(20)，但与蓄电池组容量无关，太阳翼构型不仅影响电推进角动量卸载的控制周期，还影响南北位保、东西位保的控制周期.

2 仿真算例

2.1 仿真分析的约束条件

仿真分析的约束条件包括：卫星干质量约2 500 kg，设计寿命10年；在轨正常模式整星功率2 428 W(不含电推进)；太阳阵寿命末期输出功率3.2 kW；定点经度111°E；每年南北位保所需速度增量为48 m/s；东西位保所需速度增量为2 m/s；每天角动量增量分别为1 N·m·s(双太阳翼)、40 N·m·s(单太阳翼)；锂电池组最大放电深度75%；电推力器性能参数如表1所示.

表1 典型电推力器性能参数Tab.1 Performance parameters of typical electric propulsion thrusters

推力器布局采用方式如下：4组电推力器分别位于卫星南北面，每侧布置2个推力器，每台推力器独立安装，其推力矢量由独立的矢量调节机构控制，位保时推力矢量过卫星质心；卸载工作时，矢量调节机构根据需要调整推力方向偏离质心，产生卸载力矩.

电推进工作的基本策略如下：在升交点和降交点附近进行南北位保、一轨分为相隔180°的2个开机时段进行东西位保的典型策略，如图2所示.

图2 电推进工作位置Fig.2 Work stations of electric thrusters

2.2 电推力器工作时长

将约束条件代入式(6)，得到电推力器单次最长工作时间.

将约束条件代入式(18)，得到电推力器最长工作时间

(21)

式中，Δl0为每天角动量增量，根据约束条件为1 N·m·s(双太阳翼)、40 N·m·s(单太阳翼).得出具体计算结果.

2.3 南北位保、东西位保和角动量卸载的控制周期

将约束条件代入式(14)～(16)，南北位保、东西位保和角动量卸载的控制周期

(22)

(23)

(24)

可见，充电功率UIc越大，南北位保、东西位保和卸载周期可选取的范围越宽，如图3所示.通常母线电压U为确定值(常用42 V和100 V母线电压)，当U=42 V时，可得表2所示结果.可见南北位保控制周期的选取范围最小，当充电电流Ic=5 A时，离子电推进的南北位保周期只能为1天，霍尔电推进的南北位保周期只能为1天或者2天.为了扩大南北位保的选取范围，须适当增大充电电流Ic.

对于双太阳翼的卫星，根据式(20)，取R=1.25、TMU=14 d时

(25)

式(22)、(23)和(25)存在实数解，此时推力器的额定工作时间和额定工作次数均留有25%以上的设计余量，并且满足能源平衡要求.

图3 南北位保周期与充电功率的关系Fig.3 Relations between NSSK periods and charging power

充电电流Ic/A电推进类型 5101520离子南北位保周期/天1.52.93.94.9东西位保周期/天21.038.653.766.7卸载(单翼)周期/天11.919.424.628.4单次最长工作时间/h0.841.552.162.68霍尔南北位保周期/天2.34.25.87.1东西位保周期/天31.958.180.898.5卸载(单翼)周期/天18.829.736.841.8单次最长工作时间/h0.961.752.412.97

对于单太阳翼的卫星，根据式(24)，取R=1.25、TMU=1 d时

(26)

根据表2可知，只有当TNS≥4 d、TEW≥16 d时，才能满足式(26)，此时充电电流需要达到20 A以上.

也可以适当增大帆板面积或者增大电池容量，例如，当TMU=2 d时，得到

(27)

根据表(2)可知，式(27)存在实数解，此时推力器的额定工作时间和额定工作次数均留有25%的设计余量，并且满足能源平衡要求.延长卸载周期可能需要增加姿轨控系统的资源需求，增大帆板面积或者电池容量需要增加帆板或者电池的质量，需结合工程实际进行选取，后续将展开进一步研究.

根据式(17)～(19)，结合选取的位保和卸载周期，计算得到电推力器开关机次数NNS、NEW和NMU.

根据式(10)，计算得到10年寿命期间总工作时间.

2.4 算例

如果采用增大太阳帆板面积满足电推进的功率需求，需增加帆板及电池片质量约60kg，降低了卫星平台承重能力；40%～60%的能源长时间不能有效利用，降低了整星能源利用率；单翼卫星的日角动量积累约增长一倍，在限定的资源下实现角动量卸载具有一定难度.

利用本文提出的方法，根据不同的电推进类型、帆板构型、电源系统性能，针对性的设计南北位保、东西位保和卸载周期，典型策略如下(取Ic=15 A)：

(a)双翼卫星：策略1南北位保周期3天，东西位保周期7天、角动量卸载周期14天、Q=240 A·h；策略2南北位保周期3天，东西位保周期21天、角动量卸载周期14天、Q=240 A·h；

(b)单翼卫星：策略1南北位保周期2天，东西位保周期5天、角动量卸载周期2天、Q=240 A·h；策略2南北位保周期4天，东西位保周期21天、角动量卸载周期1天、Q=360 A·h.

计算结果如表3～5所示，结果表明，留有合理设计余量的情况下，根据该方法优选得到的电推进工作策略可以满足电推力器的性能要求，并满足整星能源平衡要求；双翼卫星可利用卫星原有的电源系统配置，完成电推进系统的工作；单翼卫星对整星能源要求更高，部分情况下需要增大蓄电池组容量以满足能源平衡要求.考虑测量误差、长周期预留项等不确定因素，南北位保3天一个周期的情况下控制精度约为0.03°.

表3 典型电推进工作策略(双翼)Tab.3 Working hours of electric propulsion systems (with two solar panels)

表4 典型电推进工作策略(单翼)Tab.4 Working hours of electric propulsion systems (with single solar panel)

表5 卫星能源平衡情况(EOL)Tab.5 Power balance of satellites(EOL)

3 结 论

本文针对电推进系统的高功率需求，分析卫星能源与电推力器性能约束下的电推进南北位保、东西位保和角动量卸载的控制周期优选算法，提出基于太阳电池阵和蓄电池组联合供电的静止轨道卫星电推进在轨工作策略，得到如下结论：同等条件下霍尔电推进对于蓄电池组的放电要求更小；增大蓄电池组容量、母线电压、充电功率以及同时工作的电推力器数量可以降低蓄电池放电深度；太阳翼构型不仅影响电推进角动量卸载的控制周期，还影响南北位保、东西位保的控制周期；南北位保、东西位保和角动量卸载的控制周期选取与蓄电池组容量无关；电推力器单次最长工作时间受推力器功率和卫星能源限制，增大充电功率可以延长电推力器工作时间.仿真算例表明，在留有工程设计余量的情况下，根据该方法优选得到的电推进工作策略可以满足电推进系统的使用要求和整星能源平衡要求，提出的工作策略具有工程可行性.与采用增大太阳帆板面积的方法相比，可避免卫星平台承重能力降低(约60 kg)和整星能源利用率降低(40%～60%)，可达到高效利用电推力器和整星能源的目的.

[1] 周志成, 高军. 全电推进GEO卫星平台发展研究[J]. 航天器工程, 2015, 24(2):1-6. ZHOU Z C, GAO J. Development approach to all-electric propulsion GEO satellite platform[J]. Spacecraft Engineering, 2015, 24(2):1-67.

[2] 魏延明. 国外卫星推进技术发展现状与未来20年发展趋势[J]. 航天制造技术, 2011(2):11-16. WEI Y M. Current situation and developing direction of foreign satellite propulsion technology in the next 20 years[J]. Aerospace Manufacturing Technology, 2011(2):11-16.

[3] 周志成, 王敏, 李烽等. 我国通信卫星电推进技术的工程应用[J]. 国际太空, 2013(6):40-45.

[4] 马雪, 韩冬, 汤亮. 电推进静止轨道转移与空间环境分析[J]. 空间控制技术与应用, 2015, 41(1): 31-35. MA X, HAN D, TANG L. On the electric-propulsion-based geostationary transfer and space environmental analysis[J]. Aerospace Control and Application, 2015, 41(1): 31-35.

[5] 庞征. 中国通信卫星平台简介[J]. 国际太空, 2012(11):47-52.

[6] 边志强, 蔡陈生, 吕旺,等. 遥感卫星高精度高稳定度控制技术[J]. 上海航天, 2014, 31(3): 24-33. BIAN Z Q, CAI C S, LV W, et al. High accuracy and high stability control technology of remote sensing satellite [J]. Aerospace Shanghai, 2014, 31(3): 24-33.

[7] 董瑶海. 风云四号气象卫星及其应用展望[J]. 上海航天， 2016, 33(2):1-8. DONG Y H. FY-4 Meteorological satellite and its application prospect[J]. Aerospace Shanghai, 2016, 33(2):1-8.

[8] 吕旺，向明江,沈毅力,等. 遥感卫星动力学频谱规划[J]. 空间控制技术与应用, 2015，41(2):12-17. LYU W, XIA M J, SHEN Y L, et al. Dynamic frequency spectrum planning of remote sensing satellite[J]. Aerospace Control and Application, 2015，41(2):12-17.

[9] 李强,周志成,袁俊刚,等. GEO卫星电推力器安装位置优化研究[J]. 航天器工程, 2016, 25(4): 33-39. LI Q, ZHOU Z C, YUAN J G, et al. Optimization analysis of electric thrusters installation location on GEO satellite[J]. Spacecraft Engineering, 2016, 25(4): 33-39.

[10] 李强, 周志成, 袁俊刚, 等. GEO卫星基于电推进系统的倾角与偏心率联合控制方法[J]. 中国空间科学技术, 2015, 36(3):77-84. LI Q, ZHOU Z C, YUAN J G, et al. Inclination and eccentricity combination control method using electric propulsion for GEO satellite stationkeeping[J]. Chinese Space Science and Technology, 2015, 36(3):77-84.

[11] 马雪, 韩冬, 汤亮. 电推进卫星角动量卸载研究[J]. 中国空间科学技术, 2016, 36(1):70-76. MA X, HAN D, TANG L. Study on moment dumpling of electric propulsion satellite[J]. Chinese Space Science and Technology, 2016, 36(1):70-76.

[12] 章仁为. 卫星轨道姿态动力学与控制[M].北京: 北京航空航天大学出版社, 1998: 117-118.

Work Strategies of Electric Propulsion Systems ofGEO Satellites Based on Joint Power Supply

CHEN Xiaojie， LI Jian， ZHU Zhenhua， ZHOU Xubin， SHEN Yili

(ShanghaiInstituteofSatelliteEngineering,Shanghai201100,China)

Electric propulsion systems have huge power demands. To raise the utilization efficiency of satellite resources, work strategies of electric propulsion systems are proposed based on joint power supply from solar cells and batteries with complex engineering constrains. The impact analysis of different kinds of electric propulsions, different configurations of solar panels and power supply systems are introduced to obtain the optimization strategy during the periods of north south station keeping(NSSK), east west station keeping(EWSK) and momentum unloading(MU). Finally, simulation examples validate that reasonable work strategies can be achieved to meet the high power demands of the electric propulsion under complex engineering constrains and suitable design margin.

electric propulsion； joint power supply； work strategies； NSSK； EWSK； momentum unloading

*民用航天技术先研究项目(D010107).

2017-02-01

陈晓杰(1985—)，男，工程师，研究方向为航天器总体设计；李 鉴(1980—)，男，高级工程师，研究方向为航天器控制系统总体设计；朱振华(1978—)，男，高级工程师，研究方向为航天器总体设计；周徐斌(1975—)，男，研究员，研究方向为航天器总体设计；沈毅力(1972—)，男，研究员，研究方向为航天器总体设计.

V19

A

1674-1579(2017)03-0040-07

10.3969/j.issn.1674-1579.2017.03.007