太阳帆航天器编队维持和重构的方法研究*
王 菲,袁建平,袁 静
(西北工业大学航天飞行动力学技术重点实验室,西安 710072)
太阳帆航天器编队维持和重构的方法研究*
王 菲,袁建平,袁 静
(西北工业大学航天飞行动力学技术重点实验室,西安 710072)
针对高面质比航天器可以利用太阳光压进行轨道控制的特点,本文提出一种太阳帆航天器编队构型维持和重构的方法.该方法通过控制主从航天器太阳帆姿态角和反射系数,调整主从航天器之间的光压差,产生抵消编队成员间相对运动受到摄动差或进行轨道机动时所需的连续小推力,从而实现编队构型的维持和重构.仿真结果表明,在主航天器太阳帆的姿态角和反射系数相对固定的条件下,对于太阳同步轨道上的高面质比太阳帆航天器编队,使用滑模控制方法,能够调整编队中从航天器太阳帆的姿态角和反射系数产生推力抵消摄动力影响,达到长期维持太阳帆航天器编队构型的目的;通过开环控制方法,能够调整编队中从航天器太阳帆的姿态角和反射系数产生连续小推力,在较长时间周期内实现编队重构. 关键词: 太阳光压;太阳帆航天器;姿态角;反射系数;编队维持;编队重构
0 引 言
太阳帆航天器依靠自身面积巨大但质量轻薄的太阳帆反射太阳光可以在不消耗自身燃料的前提下获得源源不断的推力,这引起了国内外研究人员的强烈关注,并广泛应用于各类航天任务中[1-2].在利用太阳光压进行单一航天器轨道控制方面,Colombo和McInnes等[3-5]研究了利用太阳光压抵消地球J2项摄动和大气阻力等摄动力对高面质比航天器轨道演化的影响.Lücking和Colombo等[6-7]提出了利用电致变色装置来控制智能尘埃航天器的轨道.
近年来,由若干个航天器利用自然力或者稍加控制在空间形成一定构形的航天器编队,可以星间通信链路实现信息共享,统一规划各航天器的运动状态,协同完成特定的空间任务,在空间操作和自主交会等领域均有重要应用.在利用太阳帆航天器编队完成在轨服务任务方面,Williams等[8]研究了通过调整太阳帆姿态以利用太阳光压来抵消两个相邻轨道上卫星编队受到的地球扁率摄动影响造成的轨迹漂移.Smirnova等[9]讨论了利用太阳光压创建和维持一个四面体构型的卫星编队的可能性,该方法适用于日心轨道和部分高地球轨道.龚胜平等[10]提出了利用太阳帆编队飞行探测地磁尾的方法.通过改变太阳帆表面的反射系数,可以调整太阳帆的特征加速度.沐俊山等[11]在文献[8]的基础上继续研究了调整反射系数实现封闭圆相对运动,以及调整反射系数完成太阳帆的姿轨联合控制[12].侯永刚等[13]研究了利用太阳光压控制大偏心率伴飞卫星轨道,以及地球同步轨道上的四面体卫星编队[14].
近地空间长期运行的编队航天器在实际运行时,会受到各种摄动的影响,其中地球非球形摄动中的J2项摄动影响显著,并且会对相对轨道产生长期影响,严重时可能导致航天器互相碰撞.因此,本文在上述研究的基础上,提出了一种通过电驱动调整太阳帆航天器编队中从航天器太阳帆的姿态角和反射系数,来改变主从航天器受到的太阳光压之差产生连续小推力,用以抵消高阶引力项和J2摄动项对编队中航天器的相对轨迹演化影响,从而达到长期维持太阳帆航天器编队构型的目的.并且在此基础上,利用该方法采用不同的控制律可以产生连续小推力作用于编队中的从航天器,在较长时间周期内实现编队重构,以满足不同在轨服务任务的需求.
本文的第一部分介绍研究任务中所需的坐标系的定义及相互之间的转换关系,并给出了太阳帆航天器的构造设计样式.第二部分给出带有J2摄动影响的相对运动方程,并将其改写为类Lagrange形式.第三部分通过滑模控制方法设计编队维持过程的控制律;给出近圆轨道上航天器编队重构的设计方法和相应的开环控制律.第四部分在主航天器太阳帆的姿态角和反射系数相对固定的条件下,给出了控制过程中从航天器太阳帆姿态角和反射系数应满足的关系.第五部分通过数值方法验证了文中所述方法可以实现太阳帆航天器编队的队形维持和编队重构任务,并且控制过程中太阳帆姿态角和反射系数的变化都在工程允许范围内.第六部分总结本文提出的方法并对未来应用做出展望.
1 太阳帆航天器的构造与参考坐标系的定义
1.1 坐标系定义与转换关系
为了描述太阳帆航天器编队的运动情况,文中主要用到如下几个坐标系:
1)主航天器轨道坐标系osxsyszs,如图1所示:坐标原点os设在主航天器的质心,xs轴沿主航天器背离地心的方向,ys轴在轨道平面内垂直于xs轴指向飞行方向,zs轴垂直于轨道平面,xs-ys-zs构成右手正交坐标系.
2)近焦点坐标系Oxpypzp[15],如图1所示:坐标原点O设在地心,xp轴由地心指向主航天器轨道近地点,zp轴与轨道角动量方向一致,yp轴位于轨道平面内,xp-yp-zp构成右手正交坐标系.那么,轨道坐标系相对于近焦点坐标系的方向余弦矩阵为R1=Rz(θC),其中θC为主航天器的真近点角.
3)太阳光线坐标系Oxlylzl,如图1所示:在近焦点坐标系下,可以用两个方向角来描述太阳光的入射方向L,那么将近焦点坐标系先绕zp轴旋转角度λ(逆时针为正,下同),再绕yp轴旋转角度φ,即可得到太阳光坐标系,其中zl轴与太阳光入射方向L平行.当航天器运行在太阳同步轨道上时,太阳光线在近焦点坐标系中的方向角λ和φ为常值.那么,太阳光线坐标系相对于近焦点坐标系的方向余弦矩阵为R2=Ry(φ)Rz(λ).
1.2 太阳帆航天器的构造
如图2所示,为了描述太阳帆航天器的姿态变化,定义其本体坐标系osxbybzb为:坐标原点os设在航天器质心,zb轴沿太阳帆法线方向,xb轴和yb轴分别沿帆面的两个对称轴方向,xb-yb-zb构成右手正交坐标系.
假设初始时刻,航天器本体轴zb0与太阳光线(即zl轴)平行,xb0轴与yl轴平行,则太阳帆航天器初始姿态相对于太阳光线坐标系的方向余弦矩阵为R3=Rz(π/2).太阳帆航天器能够绕xb轴和yb轴分别进行-90°~90°的旋转,设某一时刻太阳帆绕yb轴转过角度α然后绕xb轴转过角度β,则此时太阳帆航天器本体坐标系相对于初始时刻的方向余弦矩阵为R4=Rx(β)Ry(α).
2 相对运动方程
在主航天器轨道坐标系中从航天器的位置矢量可以表示为:
(1)
式中,ρ=[x y z]T为从航天器在主航天器轨道坐标系中的位置矢量,ωl=[ωxωyωz]T为主航天器轨道角速度矢量,μ为地球引力常数,rC代表主航天器在地心惯性坐标系下的位置矢量,f代表除地球中心引力外的其他所有力的作用,包括摄动力和控制力.展开式(1)并考虑J2项摄动对从航天器相对运动的影响,那么相对运动动力学方程可以写为[16]
(2)
式中,rC为主航天器的地心距,u=[uxuyuz]T为维持编队构型所需的控制,Rf为从航天器的J2项摄动函数.
在实际的编队飞行任务中,由于初始化误差、未建模摄动、导航误差、推力矢量偏差等因素影响,实际轨道往往偏离标称轨道,因此必须对系统进行控制才会确保系统稳定.为了方便控制系统的设计,可以将动力学方程(2)写成类Lagrange形式
u-d
(3)
式中,C(ωz)∈R3×3,定义如下:

3 构型维持和编队重构控制器设计
3.1 构型维持设计
滑模变结构控制是一类特殊的非线性控制,与其它控制的不同之处在于系统的“结构”并不固定,可以在动态过程中根据系统当前的状态有目的地不断变化,迫使系统按照预定“滑动模态”的状态轨迹运动[17].本文借鉴滑模变结构控制对非线性系统和不确定性摄动鲁棒性强的特点,将其用于非线性和摄动条件下航天器编队相对轨道的精确保持.设计如下形式的滑模面:
(4)
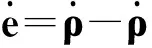
为了分析滑动模态的稳定性,定义Lyapunov函数为
(5)
对其求导,有
(6)
由Lyapunov稳定性理论,滑动模态渐近稳定.
为降低抖振,采用指数趋近律到达滑模面条件,并选取饱和函数替代符号函数来平滑控制量
(7)
式中,ε,k∈R3×3>0,为正定对称常值矩阵.饱和函数sat(·)定义为
(8)
式中,Δ为“边界层”.
综合式(3)、(4)、(7)、(8)可以得到控制律
(9)
为了验证控制律(9)的稳定性,定义Lyapunov函数:
(10)
将控制律(9)代入式(10)并求导,有
-sTks≤0
(11)
根据Lyapunov函数稳定性定理,上述设计的滑模控制器式(11),可以保证滑模控制系统全局渐进稳定.
3.2 编队重构设计
在航天器编队飞行过程中,编队的构型往往需要根据在轨服务任务的需求做出相应的变化,即进行编队重构.近圆轨道上的航天器相对运动方程可以由C-W方程给出,编队中从航天器相对于主航天器的运动可以近似为3个简谐运动的叠加,因此简单航天器编队构形重构问题可以描述为以下相对运动轨道的调整问题,即

(12)

(13)
式中,γ1、γ2、ξ1、ξ2为控制参数.对于相位无约束重构问题,各航天器的控制是一致的,只需求解以下代数方程组:
(14)
式中,TD为重构时间.
4 太阳帆姿态和反射系数的调整
太阳光压产生的摄动加速度为:
(15)
式中,pSR=4.56×10-6N/m2为距太阳1 AU距离上的光压常数,cR(1 利用太阳帆进行轨道控制,就要求主从航天器的太阳光压加速度之差与控制加速度相等,即 aSRP_D-aSRP_C=u, (16) 式中,下标C和D分别代表主从航天器(下同),方向余弦矩阵中的系数分别为r11=cosφcos(θ-λ), r21=-cosφsin(θ-λ),r31=-sinφ,r12=sin(θ-λ),r22=cos(θ-λ),r32=0,r13=sinφcos(θ-λ), r23=-sinφsin(θ-λ),r33=cosφ.本文中假设主航天器太阳帆的姿态角和反射系数相对固定,即aSRP_C=[axCayCazC]T为常矢量,那么欲达到控制目的,由式(16)可得,需要调整从航天器太阳帆姿态角αD和βD以及反射系数cR_D满足以下关系: 1)当u+aSRP_C≠0时, (17) 由于文中α和β的取值范围都为-90°~90°,所以上式可以唯一确定太阳帆姿态角; 2)当u+aSRP_C=0时,αD=±π/2,βD=±π/2,cR_D=1.5(取其他1~2之间的任意值也可). 5.1 队形维持仿真校验 设置主航天器轨道初始参数如表1所示.根据描述主航天器位于任意椭圆轨道上的从航天器的相对运动方程的无长期漂移要求[19-20],设置从航天器在主航天器轨道坐标系下的初始位置和速度分别为: 从航天器的其他初始参数与主航天器相同. 仿真校验过程中滑模控制中的参数可以选取为:α=diag{3,3,3}×10-5,ε=diag{3,3,0.1}×10-7,k=diag{5,2,1}×10-3,Δ=diag{5,5,5}×10-5.仿真时间为30天. 表1 主航天器初始轨道参数Tab.1 Initial orbital parameters of the chief spacecraft 图3~7给出了编队维持过程中相应的仿真结果曲线.由图 3的绕飞轨迹可以看出,当考虑J2摄动和地球引力非线性项时,从航天器的绕飞轨迹会沿其速度方向产生明显的漂移,且严重时会有与主航天器碰撞的危险(见灰色虚线轨迹演化),而控制后从航天器的相对轨迹基本保持在初始轨迹附近(见黑色实线轨迹演化),由此说明文中方法可以实现长期的相对构型维持.由图4可以看出,在整个控制过程中位置误差能够保持在8 m以下,说明控制效果可以达到工程要求. 由图5和图6可以看出,在编队维持过程中从航天器姿态角调整范围在0.5 rad内,由点划线方框内的24小时放大图可以看出,一天之内姿态角变化相对平缓易于操作实现.由图7可以看出,从航天器反射系数变化可以满足工程要求的反射系数范围,即1 5.2 编队重构仿真校验 设置主航天器初始轨道参数如表1所示.设置重构时间为TD=105s,从航天器初始时刻相对轨道和期望重构后的相对轨道分别表示为: 图8~11给出了重构过程中相应的仿真结果曲线.由图8的重构轨迹可以看出,通过调整从航天器太阳帆姿态角和反射系数以利用太阳光压产生连续小推力,可以使从航天器由初始编队构型沿螺旋线转移轨迹在设定的时间内达到预定的目标构型,即运用文中所述方法可以在已设定的时间内实现航天器编队重构的目的. 由图9和图10可以看出,重构过程中姿态角调整范围在0.1 rad内,且变化较为平缓,易于操作实现.由图11可以看出,从航天器反射系数变化可以满足工程要求的反射系数范围,即1 本文针对太阳帆航天器编队的维持和重构问题,设计了具备2个旋转自由度并且表面反射涂层材料的反射系数可以通过电激励方式改变的太阳帆,在主航天器太阳帆的姿态角和反射系数相对固定的条件下,分别采用滑模控制和开环控制方法设计控制律,给出了通过主动控制从航天器太阳帆的姿态角和反射系数达到构型维持目的的方法和编队重构目的的方法.仿真分析表明:在无燃料消耗的情况下,通过太阳光压控制的编队可长期维持相对稳定的构型,也可以在较长时间内实现编队重构,并且在构型维持和编队重构的整个控制过程中从航天器太阳帆的姿态角和反射系数变化都在要求的合理范围内.相比于普通航天器利用星载燃料产生推力实现编队维持和重构,本文方法具有节省燃料、长期维持某种编队构型、执行多次重构任务、延长航天器使用寿命等优点,是未来航天器发展的趋势. [1] MACDONALD M, MCINNES C. Solar sail science mission applications and advancement[J]. Advances in Space Research, 2011, 48(11): 1702-1716. [2] SAILING S T. Dynamics, and mission applications[M]. New York: Springer-Verlag, 1999. [3] COLOMBO C, MCINNES C. Orbital dynamics of “smart-dust” devices with solar radiation pressure and drag[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(6): 1613-1631. [4] COLOMBO C, LÜCKING C, MCINNES C R. Orbital dynamics of high area-to-mass ratio spacecraft with J2 and solar radiation pressure for novel Earth observation and communication services[J]. Acta Astronautica, 2012, 81(1): 137-150. [5] COLOMBO C, MCINNES C R. Orbit design for future SpaceChip swarm missions[C]//The 61stAeronautical Congress. New York: IAC, 2010. [6] LÜCKING C, COLOMBO C, MCINNES C R. Electrochromic orbit control for smart-dust devices[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(5): 1548-1558. [7] COLOMBO C, LÜCKING C, MCINNES C R. Orbit evolution, maintenance and disposal of SpaceChip swarms through electro-chromic control[J]. Acta Astronautica, 2013, 82(1): 25-37. [8] WILLIAMS T, WANG Z S. Uses of solar radiation pressure for satellite formation flight[J]. International Journal of Robust and Nonlinear Control, 2002, 12(2-3): 163-183. [9] SMIRNOV G V, OVCHINNIKOV M, GUERMAN A. Use of solar radiation pressure to maintain a spatial satellite formation[J]. Acta Astronautica, 2007, 61(7): 724-728. [10] GONG S, YUNFENG G, LI J. Solar sail formation flying on an inclined Earth orbit[J]. Acta Astronautica, 2011, 68(1): 226-239. [11] MU J, GONG S, LI J. Reflectivity-controlled solar sail formation flying for magnetosphere mission[J]. Aerospace Science and Technology, 2013, 30(1): 339-348. [12] MU J, GONG S, LI J. Coupled control of reflectivity modulated solar sail for GeoSail formation flying[J]. Journal of Guidance, Control, and Dynamics, 2014, 38(4): 740-751. [13] 侯永刚, 赵长印, 张明江, 等. 利用太阳光压的大偏心率伴飞卫星轨道控制[J]. 天文学报, 2016, 57(1): 52-65. HOU Y G, ZHAO C Y, ZHANG M J, er al. Orbit control of fly-around satellite with highly eccentric orbit by using solar radiation pressure[J]. Acta Astronomica Sinica, 2016, 57(1): 52-65. [14] HOU Y G, ZHANG M J, ZHAO C Y, et al. Control of tetrahedron satellite formation flying in the geosynchronous orbit using solar radiation pressure[J]. Astrophysics and Space Science, 2016, 361(4): 1-11. [15] CURTIS H D. 轨道力学[M]. 周建华, 徐波, 等译. 北京: 科学出版社, 2009. [16] 杏建军. 编队卫星周期性相对运动轨道设计与构形保持研究[D]. 长沙: 国防科学技术大学, 2007. XING J J. Study on formation design and stationkeeping of spacecraft formation flying[D]. Changsha: National University of Defense Technology, 2007. [17] 刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3): 407-418. LIU J K, SUN F C. Research and development on theory and algorithms of sliding mode control[J]. Control Theory & Applications, 2007, 24(3): 407-418. [18] 孟云鹤. 近地轨道航天器编队飞行控制与应用研究[D]. 长沙: 国防科学技术大学, 2006. MENG Y H. Research on control and application of LEO spacecraft formation flying[D]. Changsha: National University of Defense Technology, 2006. [19] INALHAN G, TILLERSON M, HOW J P. Relative dynamics and control of spacecraft formations in eccentric orbits[J]. Journal of guidance, control, and dynamics, 2002, 25(1): 48-59. [20] FENG W, XIBIN C, XUEQIN C. On-orbit-servicing spacecraft flyaround orbit design and LQR keep control in eccentric orbits[C]//The 2ndIEEE Conference on Industrial Electronics and Applications. New York: IEEE, 2007. Formation Keeping and Reconfiguration for Solar Sail Spacecraft WANG Fei, YUAN Jianping, YUAN Jing (NationalKeyLaboratoryofAerospaceFlightDynamics,NorthwesternpolytechnicalUniversity,Xi’an710072,China) In this paper, a new method for maintaining and reconfiguring the solar sail spacecraft formation is proposed, based on the fact that the orbit of the high area-to-mass ratio spacecraft can be controlled via solar radiation pressure. The difference of solar radiation pressure on the formation members can be adjusted by controlling attitude angles and reflection coefficient of the chief and deputy solar sail spacecraft, and the continuous low thrust can be produced for counteracting the perturbation difference in relative motion of formation constellation members or orbital maneuvers, thus achieving the purpose of formation configuration maintenance and formation reconfiguration. Under the condition that attitude angles and the reflection coefficient of the chief solar sail spacecraft are relatively fixed, the simulation results show that the purpose of long-term formation keeping of solar sail spacecraft formations in Sun-synchronous orbit can be achieved by sliding mode control, which is able to counteract the perturbation difference in relative motion of formation constellation members by controlling attitude angles and reflection coefficient of the deputy solar sail spacecraft. And in the same way, formation reconfiguration can be achieved by using open-loop control after long period. solar radiation pressure; solar sail spacecraft; attitude angle; reflection coefficient; formation keeping; formation reconfiguration *国家自然科学基金资助项目(11472213)和国家航天飞行动力学技术重点实验室开放基金资助项目(2015afdl015). 2016-11-12 王 菲(1991—),女,硕士研究生,研究方向为航天飞行动力学与控制;袁建平(1957—),男,教授,研究方向为飞行力学;袁 静(1967—),女,高级工程师,研究方向为计算机软件和计算机仿真. V412.4 A 1674-1579(2017)03-0007-08 10.3969/j.issn.1674-1579.2017.03.002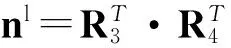
5 仿真校验

6 结 论

