三维充液航天器的位置和姿态联合控制*

王泽国，张洪华,2，胡锦昌，2

(1.北京控制工程研究所，北京 100190； 2.空间智能控制技术国家级重点实验室，北京 100190)



三维充液航天器的位置和姿态联合控制*

王泽国1，张洪华1,2，胡锦昌1，2

(1.北京控制工程研究所，北京 100190； 2.空间智能控制技术国家级重点实验室，北京 100190)

考虑充液月球着陆器悬停避障阶段的控制问题，采用三维球摆作为液体晃动部分的等效模型.针对球摆与刚体耦合的三维动力学模型，给出动力学模型的矢量方程及各矢量在本体系的投影坐标，设计位置和姿态联合控制器.所设计的控制器可以稳定航天器刚体的位置和姿态，且只依赖刚体的位置和姿态，不依赖晃动角或者动力学方程，利于工程应用.利用LaSalle不变原理分析闭环系统的稳定性，给出期望姿态为竖直时系统渐近稳定的控制器参数选择依据.最后数值仿真验证控制方法的有效性. 关键词： 液体晃动；位置和姿态联合控制；三维球摆；充液航天器

0 引 言

航天器一般采用液体作为推进剂，在机动过程中，液体推进剂在贮箱内的运动不免对航天器本体造成影响，甚至引起不稳定[1]，因此液体晃动是航天器控制器设计中需要重点关注的问题.

为了得到液体晃动的解析解需要求解偏微分方程，一般难以求解.控制器设计关心的是航天器机动时液体对航天器本体的力和力矩影响，液体晃动一般等效成质量弹簧或者单摆模型，继而利用牛顿欧拉法或者拟拉格朗日函数法建立动力学模型[2].

经典的液体晃动影响等效为二维模型，在小幅度线性晃动的假设下，等效模型参数可以由贮箱形状通过解析表达式得到[3].针对二维等效模型与航天器刚体耦合模型，文献[4]仅考虑姿态控制的情况，对二维等效模型进行线性化，得到单输入单输出的传递函数模型，然后设计滤波器得到姿态控制器.此方法在线性范围内可以利用根轨迹或者Bode图分析闭环线性系统性能，但是对于大范围机动情况和多入多出情况难以分析.文献[5]利用分层滑模控制方法设计了姿态控制器，并且对闭环非线性系统进行了稳定性分析，但需要精确动力学模型.文献[6]中为了描述液体在贮箱内多个平面的运动以及非线性特性，需要建立三维等效模型.文献[7-8]将液体等效为三维球摆，利用Newton-Euler方法给出了与航天器刚体结合的耦合模型.针对三维等效模型与航天器刚体耦合模型，文献[9]利用欠驱动控制设计方法给出了控制器设计，利用Lyapunov方法分析了三维模型的闭环稳定性.此方法需要精确已知耦合动力学以及参数，然而液体晃动是通过力学模型等效的，并没有传感器测量获得液体晃动的等效状态.文献[10]利用反馈线性化方法设计刚体控制器，并利用自适应神经网络处理未知动力学部分.但此方法缺少对闭环系统的稳定性分析.

本文考虑月球着陆器悬停避障阶段的液体晃动抑制与控制问题[11].考虑液体晃动的三维球摆等效模型，针对液体与航天器刚体的三维耦合模型，设计位置和姿态联合控制器.控制器仅需已知刚体的位置和姿态及其速度和角速度，不需已知晃动角信息.通过LaSalle不变原理分析给出闭环系统是渐近稳定的条件.

1 问题描述

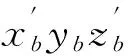
(1)

(2)

(3)

其中：

(ωb+ωp)×[(ωb+ωp)×rp]

为了得到动力学方程的坐标表示，将式(1)～(3)中各个矢量投影到本体坐标系

(4)

下面采用四元数描述航天器本体的姿态.设本体系Obxbybzb相对于惯性系OIxIyIzI的四元数为

(5)

其中，

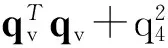
Cbi=

航天器的位置Rb一般是在惯性系下表示为Rbi=[RbixRbiyRbiz]T，而式(1)是在本体系下表示Rb，其转换关系为

Rb=CbiRbi

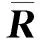
2 控制器设计

(6)

则式(4)中控制器设计为

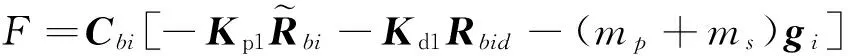
(7)

其中控制器参数Kp1,Kd1,Kp2,Kd2∈R3×3为正定矩阵，gi=[-ge0 0]T.

3 稳定性分析

下面给出针对系统(1～3)和控制器(7)的闭环稳定性分析[13-14].

(8)

需要说明的是，式(8)是为下面证明需要而给出的，本文不需要式(8)的显式形式.

下面考虑函数

将V其对时间求导可得

≤0

由Kd1和Kd2是正定矩阵，ξη1，ξη2>0，可知

即状态的导数和二阶导数为零.代入动力学方程(1～3)中并考虑式(7)可得

可知

(9)

若控制器(7)参数选择为对角矩阵

其中kp2x,kp2y,kp2z>0，则由式(9)可知有

(10)

显然式(10)存在解q=[0 0 0 1]T.并且当控制器参数满足

(11)

4 数值仿真

仿真中参数如下：

Js=diag{8.452,10.767,8.727} kg·m2，ms=300 kg,mp=30 kg,ge=1.622 m/s2，ξ=0.000 2,Lp=0.228 m,rtx=-0.4 m.初始状态为：Rbi=[100 0 0]T,q=[0 sin(π/36)，cos(π/36)]T，α1=α2=0.

考虑月球着陆器悬停避障的任务需求[11]，目标位置和姿态为

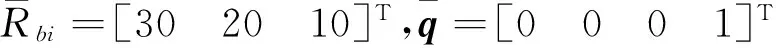
由于仿真中所考虑情况为rtx<0，所以控制器(7)参数满足正定即可，因此设计参数为

Kp1=diag{3.3,3.3,3.3},

Kd1=diag{52.8,52.8,52.8}，

Kp2=diag{10,10,10},Kd2=diag{20,20,20}.

仿真结果如图3～8所示.图3给出了航天器刚体质心的位置，可见航天器可以渐近到达给定的目标位置.航天器的姿态四元数由图4给出，可知姿态同样渐近达到目标姿态，即竖直悬停状态.图5给出了角速度.图6给出了球摆的摆角曲线，在运动初始时有较大幅值的摆动，很快衰减后稳定在零点.最后图7和图8分别给出了控制力和控制力矩曲线.仿真结果显示所设计的控制器可以满足航天器悬停避障的要求.

5 结 论

考虑了充液月球着陆器的悬停避障问题.采用球摆等效液体晃动对刚体的影响，针对三维球摆与刚体的耦合动力学模型，设计了位置和姿态联合控制器，使得航天器可以到达指定的位置和竖直姿态.所设计的控制器仅依赖于刚体的位置与姿态.通过分析给出系统渐近稳定的条件.仿真验证所设计的控制器.

[1] NICHKAWDE C, HARISH P M, ANANTHKRISHNAN N. Stability analysis of a multibody system model for coupled slosh-vehicle dynamics[J]. Journal of Sound and Vibration, 2004, 275(3-5): 1069-1083.

[2] ABRAMSON H N. The dynamic behavior of liquids in moving containers[R].Washington D.C.: NASA, 1966.

[3] IBRAHIM R A. Liquid sloshing dynamics theory and applications[M]. New York: Cambridge University Press, 2005.

[4] WIE B. Thrust vector control design for a liquid upper stage spacecraft[J]. Journal of Guidance, Control, and Dynamics, 1985, 8(5): 566-572.

[5] 杜辉, 张洪华. 一类带液体晃动航天器的姿态控制[J]. 空间控制技术与应用, 2010, 36(2): 25-30. DU H, ZHANG H H. Attitude control for a kind of spacecraft with fuel slosh[J]. Aerospace Control and Application, 2010, 36(2): 25-30.

[6] KANA D D. Validated spherical pendulum model for rotary liquid slosh[J]. Journal of Spacecraft and Rockets, 1989, 26(3): 188-195.

[7] 苗楠, 李俊峰, 王天舒. 横向激励下液体大幅晃动建模分析[J]. 宇航学报, 2016, 37(3): 268-274.

MIAO N, LI JF, WANG T S. Modeling analysis of large-amplitude liquid sloshing under lateral excitation[J]. Journal of Astronautics, 2016, 37(3): 268-274.]

[8] MIAO N, LI J F, WANG T S. Large-amplitude sloshing analysis and equivalent mechanical modeling in spherical tanks of spacecraft[J]. Journal of Spacecraft and Rockets, 2016, 53(3): 500-506.

[9] HERVAS J R, REYHANOGLU. Thrust-vector control of a three-axis stabilized upper-stage rocket with fuel slosh dynamics[J]. Acta Astronautica, 2014, 98: 120-127.

[10] DE WEERDT E, VAN KAMPEN E, VAN GEMERT D,et al. Adaptive nonlinear dynamic inversion for spacecraft attitude control with fuel sloshing[C]//AIAA Guidance, Navigation and Control Conference and Exhibit.Washiongton D.C.: AIAA, 2008.

[11] 张洪华, 梁俊, 黄翔宇, 等. 嫦娥三号自主避障软着陆控制技术[J]. 中国科学: 技术科学, 2014, 44(6): 559-568. ZHANG H H, LIANG J, HUANG X Y, et al. Autonomous hazard avoidance control for Chang’E-3 soft landing[J]. Science China: Technological Sciences, 2014, 44(6): 559-568.

[12] 祝乐梅, 岳宝增. 充液航天器姿态的自适应非线性动态逆控制[J]. 动力学与控制学报, 2011, 9(4): 321-325. ZHU L M, YUE B Z. Adaptive nonlinear dynamic inversion control for spacecraft attitude filled with fuel [J]. Journal of Dynamics and Control, 2011, 9(4): 321-325.

[13] KELKAR A G, JOSHI S M, ALBERTS T E. Passivity-based control of nonlinear flexible multibody systems[J]. IEEE Transactions on Automatic Control, 1995, 40(5): 910-914.

[14] WANG H L, XIE Y C. Passivity based attitude control of rigid bodies[J]. Asian Journal of Control, 2014, 16(3): 802-817.

[15] KHALIL H K. Nonlinear systems[M]. Upper Saddle River, New Jersey: Prentice Hall, 2002.

Passive Control for a Three-Dimensional Liquid-Filled Spacecraft

WANG Zeguo1, ZHANG Honghua1,2, HU Jinchang1,2

(1.BeijingInstituteofControlEngineering，Beijing100190，China；2.ScienceandTechnologyonSpaceIntelligentControlLaboratory,Beijing100190,China)

The hazard-avoidance control for a liquid-filled lunar lander is considered in this paper. A three-dimensional spherical pendulum is used for the mechanical equivalent model of the liquid sloshing. Considering the three-dimensional dynamics combined of spherical pendulum and rigid body of spacecraft, the vector dynamics equations are given as well as the projected coordinates of each vector variables. With these equations, a combined position and attitude controller is designed, which can stabilize the position and attitude of the rigid body. Moreover, this controller only depends on the position and attitude of rigid body, and independent of liquid sloshing angle or sloshing dynamics. It thus leads to the convenience for the practical applications. The stability of closed-loop system is given via LaSalle invariance principle, and the control parameters are suggested for the asymptotical stability of the system when the reference vertical attitude is chosen. Finally the effectiveness of the proposed control is validated via numerical simulations.

liquid sloshing； combined position and attitude control； spherical pendulum； liquid-filled spacecraft

*国家自然科学基金资助项目(61403031,61603038).

2017-02-01

王泽国(1988—)，男，博士研究生，研究方向为航天器制导与控制；张洪华(1963—)，男,研究员,研究方向为月球探测器制导、导航与控制技术等；胡锦昌(1984—)，男，工程师，研究方向为月球着陆器的制导与控制方法等.

V448.22

A

1674-1579(2017)03-0015-06

10.3969/j.issn.1674-1579.2017.03.003