带约束拉杆L形方钢管混凝土组合异形柱的受力研究

吴邦睿，杨秀荣，樊 成

(大连大学 建筑工程学院， 辽宁 大连 116622)

带约束拉杆L形方钢管混凝土组合异形柱的受力研究

吴邦睿，杨秀荣，樊 成

(大连大学 建筑工程学院， 辽宁 大连 116622)

为研究对拉约束拉杆对组合柱性能的影响，针对L形组合异形柱设置不同类型的约束拉杆、不同强度材料等进行数值模拟，对比该类型下的相应试验结果，分析验证了对拉约束拉杆对L形组合异形柱的性能改善作用，得到了对拉约束在柱延性及承载力方面的积极影响效果。最后基于线性回归分析的理论计算方法表现出了和数值结果较高的一致性，建立了具有较高参考价值的带约束拉杆的组合异形柱承载力计算公式。

组合柱；钢管混凝土；有限元分析；延性

钢筋混凝土结构以其良好的力学性能和低廉的造价等优点，自问世以来极大地推动了建筑行业的发展。随着近些年建筑对空间和美观的要求越来越重视，纯粹的钢筋混凝土结构已经无法满足新的建筑标准，一种新型的建筑形式：组合异形柱应运而生[1-2]。近年来，组合异形柱以灵活的截面形式以及较高的承载能力[3]，获得了广泛的市场认可，该结构形式在空间布置、结构承载性能、施工技术应用等方面崭露头角[4-6]。

组合异形柱具有不同的截面形式，具有很多令人称道的优点[7]，但单肢柱中钢管和混凝土的协同工作一直备受诟病[8-9]。其单肢柱中钢管对混凝土的约束作用主要集中在角部，周边较低，因此导致承载能力相应降低[10-11]。

改善这一问题，可促进钢管与混凝土的协同作用进而提高组合柱的性能。根据以往的施工经验，在混凝土结构中，钢筋和混凝土正是因为较好的协同工作性而被广泛使用[12-13]，因此笔者设想在单肢柱中相应的距离，设置采用钢筋制作的对拉约束拉杆，对拉拉杆采用螺栓形式与钢管连接成为整体。本文针对采用对拉约束拉杆后的L形组合异形柱进行分析验证。

1 试件及有限元模型设计

带约束组合异形柱不同于一般的混凝土柱，其单肢柱为内部填充混凝土配合外部钢管，并采用对拉拉杆提高核心混凝土与钢管的协同工作性能，其本构关系亦不相同[14]。蔡健等[15]人采用侧向等效应力概念，提出了轴压作用下带约束混凝土的本构关系。本文根据该本构关系建立了有限元模型。

1.1 试件设计

基于该课题的相关研究成果[16]，结合传统结构形式(见图1)，设置约束拉杆(见图2(c))，建立L形方钢管混凝土组合异形柱。

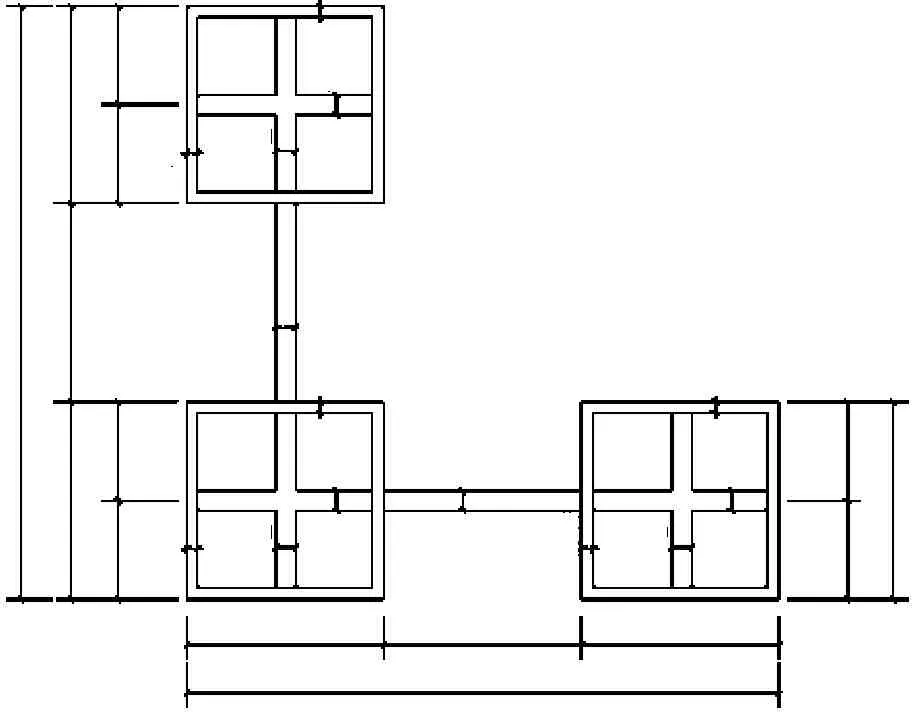
图1 柱截面布置

约束混凝土选用八节点六面体线性减缩积分实体单元(C3D8R)，钢管和缀条采用四节点四边形应变线性减缩积分壳单元(S4R)，约束拉杆采用杆单元(T2)，混凝土与钢管采用的是摩擦硬接触，摩擦系数为0.6，钢管与缀条、约束拉杆之间建立“Tie”关系。

其中，各组成部分和整体三维有限元模型见图2。

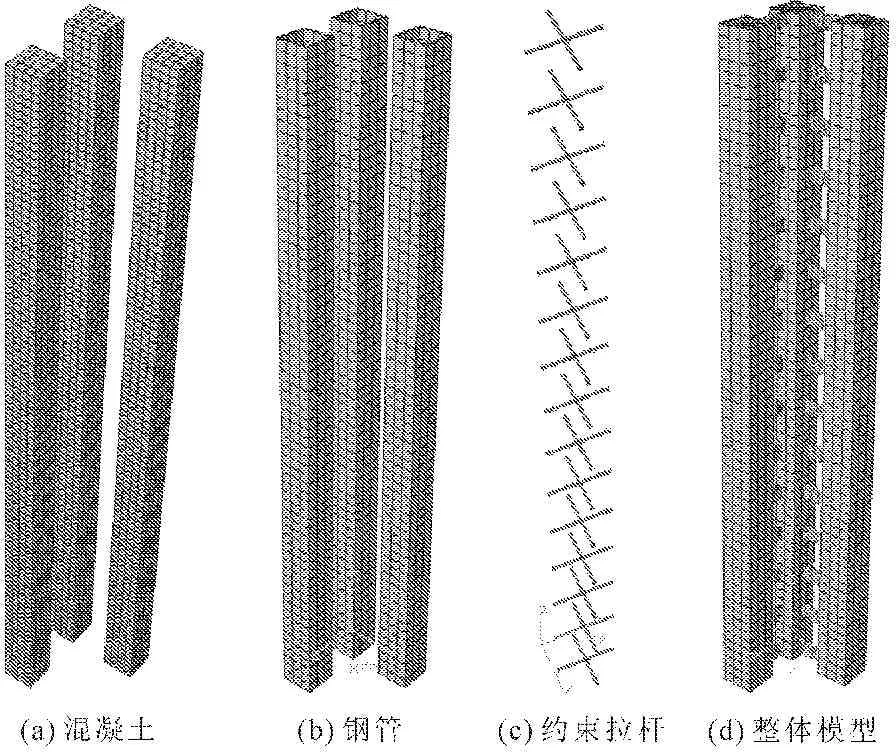
图2 有限元模型

1.2 试件材料参数

本实验中钢管与柱间连接缀条采用Q235B钢材，缀条与钢管采用焊接连接，焊条使用E43系列。柱内约束拉杆采用HRB335钢筋，与钢管使用螺栓进行连接。柱构件在浇筑混凝土后置于20℃±2℃，湿度为95%RH条件下养护28 d。某些材料的相关参数如表1、表2所示。

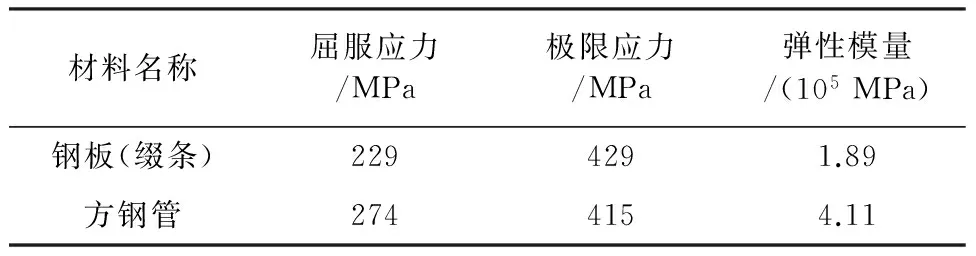
表1 钢材料参数

表2 混凝土力学参数

1.3 边界条件及荷载的施加

带约束拉杆L形方钢管混凝土组合异形柱长柱构件的底面节点三向铰接，顶面节点的两向自由铰接，使柱子处于两端铰接的约束状态，在构件顶部形心处施加负向位移。

2 数值模拟结果验证

通过有限元计算分析，将试验得到的应力-应变曲线与模拟的数值进行对比分析结果见图3，由图3可以看出，试验值前期上升过程起步较快，在早期相同应变对应的应力较大，达到峰值后平缓下降。ABAQUS模拟的数值结果早期相同应力作用下产生的应变大于试验值，后期应变程度反而略小于试验值。总体来说，两者峰值大小基本相同，达到57 MPa左右，试验值和计算值都说明采用对拉约束后承载力得到相应提高；二者曲线的整体走向也十分相似，都有明显的塑形变形阶段，也展现出了较好的延性。

图3 应力-应变曲线试验结果与计算结果对比图

图4为通过增加约束拉杆后L形方钢管混凝土组合异形柱的承载力和延性改善曲线，该荷载-位移曲线显示随着荷载的增加形变相对原试验结构变形较小，承载力极限3 700 kN高于原结构形式，且此时的竖向位移4 mm也小于原试验形变。由此可知增加约束拉杆可以有效改善柱子的力学性能。

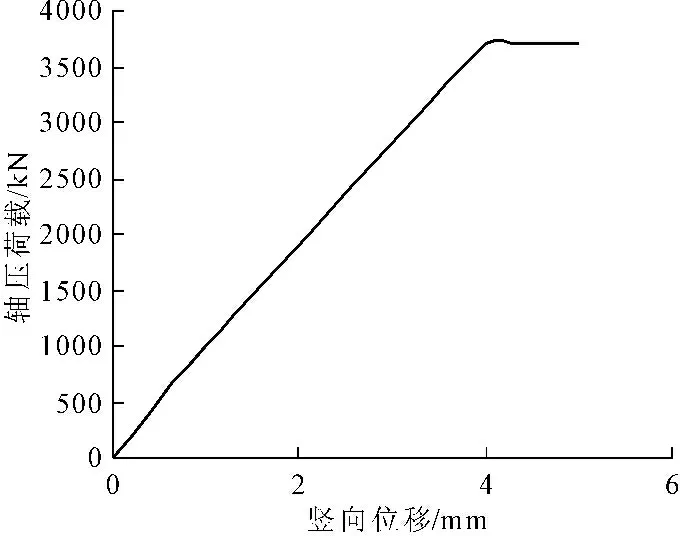
图4 荷载-位移曲线

3 影响异形柱力学性能对比分析

3.1 关于约束拉杆间距的对比分析

分别对不同间距的带约束拉杆的L形方钢管混凝土组合异形柱进行数值分析，可得荷载-应变曲线，如图5所示。

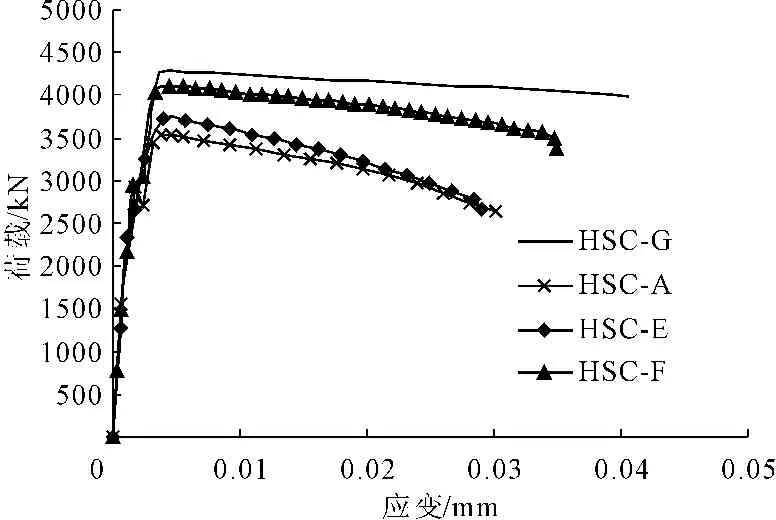
图5 不同约束拉杆间距的荷载-应变关系曲线

图5为不同间距的约束拉杆对荷载和应变的影响曲线，其中HSC-A、HSC-E、HSC-F、HSC-G为不同的拉杆间距，A柱间距较大，G柱间距较小。由图5中曲线可以得知，约束拉杆的间距越小其承载能力越高。同时，对比发现，间距越小的柱子形式，表现出了更好的变形能力，说明在L形组合柱中设置对拉约束可以有效改善柱子变形能力，提高柱子延性。

3.2 关于混凝土抗压强度的对比分析

混凝土的抗压强度是影响柱子性能的一个重要参数，本文对不同的混凝土抗压强度下柱的承载能力进行了数值模拟，得到曲线图见图6。

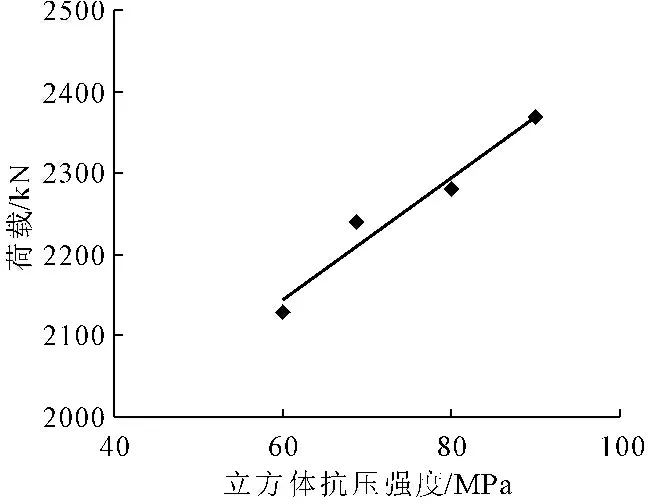
图6 不同混凝土抗压强度的极限承载力曲线

由图6可以看出，随着混凝土强度的提高，承载能力也相应增大，该曲线近似为一条直线，由此可知该结构形式下，随着混凝土强度的提升结构整体表现出较好的统一性。

3.3 关于钢管屈服强度的对比分析

分别对不同钢管屈服强度的带约束拉杆L形方钢管混凝土组合异形柱进行数值分析，如图7所示。

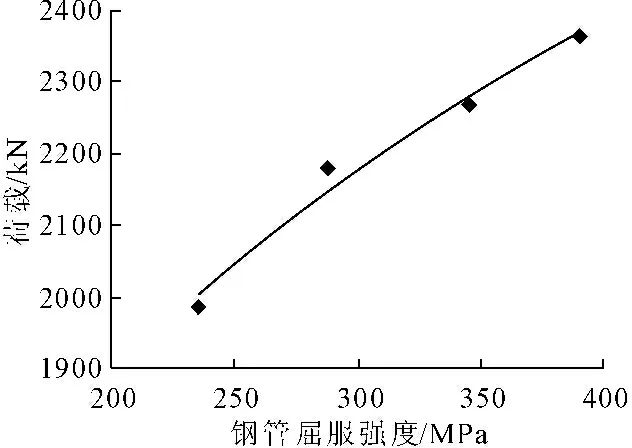
图7 不同钢管屈服强度的极限承载力曲线

由图7可以看出钢管屈服强度和带约束拉杆L形方钢管混凝土组合柱的承载力成正比，其承载能力随钢管屈服强度的增加而增加。该因素对柱子的延性和Ec改变不大。

3.4 不同拉杆间距与极限承载力的关系

拉杆间距与极限承载力分析结果见图8。由图8可知，拉杆间距由50 mm增大为200 mm的过程中，柱子承载能力呈下降趋势，随着约束拉杆间距的增大，柱延性不断减小，由此，设置对拉拉杆的确可以改善柱子延性。

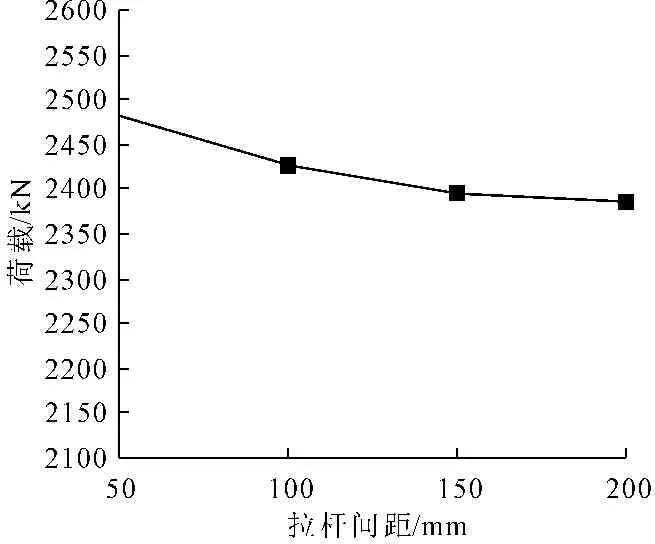
图8 约束拉杆间距的影响

4 带约束拉杆L形组合短柱的承载力计算公式

结合文献[1]，总结带约束拉杆L形方钢管混凝土组合异形柱的承载力公式：

Nu=fayAs+φcfckAc

(1)

式中：φc为核心混凝土抗压强度提高系数；As为钢管截面面积；Ac为核心混凝土截面面积。

考虑到拉杆约束系数ξ，混凝土抗压强度fck，钢管屈服强度fay，钢管壁厚t以及截面尺寸b对混凝土抗压强度均有不同程度的作用[17-18]。结合本文数值分析结果，可得到关于抗压强度的影响因素φc公式：

φc=μcμaμtμb(1+3.168ξ)

(2)

式中：μc为混凝土抗压强度fck修正系数；μa为钢管屈服强度fay修正系数；μt为钢管壁厚t修正系数；μb为截面尺寸b修正系数；as为约束拉杆的横向间距；bs为约束拉杆的纵向间距；ξ为拉杆约束系数。

ξ=fyAs/fckasbs

(3)

(4)

(5)

(6)

(7)

计算结果与试验结果比较如图9所示，数值模拟的结果整体略高于计算结果，二者散点分布交错融合，其各自相应的趋势线角度相差不大，基于以上分析说明计算结果和数值结果能较好吻合，数据表现良好。

图9 约束拉杆间距的影响

5 结 论

(1) 通过对L形组合异形柱设置对拉拉杆约束，柱延性和承载力得到提高，表明对拉约束可以在一定程度上改善柱子的延性和承载能力，设置对拉约束的方式可以向类似的结构构件推广应用。

(2) 试验数据和数值模拟结果表明不同的约束拉杆间距会对柱的延性产生不同的作用效果，在间距相对较小时，提高延性表现较好。

(3) 本文对于对拉约束对延性和承载力的分析仅出于整体趋势方向，笔者认为该间距应为一个有效的范围，基于这方面的研究还需要更深入的试验进行分析研究。

[1] 江见鲸.钢筋混凝土结构[M].北京:中国建筑工业出版社,1998.

[2] Popovics S. A numerical approach to the complete stress-strain curve of concrete[J]. Cement and Concrete Research, 1973,3(5):583-599.

[3] 廖祥盛.带约束拉杆方形钢管混凝土短柱抗震性能研究[D].广州：华南理工大学,2014.

[4] 陈志华,杜颜胜,吴 辽,等.矩形钢管混凝土结构研究综述[J].建筑结构,2015,45(16):40-46，76.

[5] 王文博,王建伟.钢管混凝土研究进展[J].工业建筑,2011(S1):332-334.

[6] 王文达,朱彦鹏.钢管混凝土结构研究及应用的关键技术[J].甘肃工业大学学报,2003,29(3):113-117.

[7] 陈志华,荣 彬.L形方钢管混凝土组合异形柱的轴压稳定性研究[J].建筑结构,2009,39(6):39-42.

[8] 宋 力,杨秀荣.双层高强箍筋约束高强混凝土不同截面柱的受力[J].辽宁工程技术大学学报(自然科学版),2016,35(12):1449-1453.

[9] 陈 叶,刘 忠,李 佩,杨龙刚.L形混凝土偏心受压柱力学性能数值分析[J].水利与建筑工程学报,2016,14(3):167-171，225.

[10] 朱昌宏.带约束拉杆方形和矩形截面钢管混凝土短柱承载力与延性[D].广州：华南理工大学,2010.

[11] 陈兰响,关 萍,刘晴晴.基于ABAQUS分析型钢-圆钢管混凝土的力学性能[J].水利与建筑工程学报,2015,13(2):15-19.

[12] 蔡 健,孙 刚.轴压下带约束拉杆L形钢管混凝土短柱的试验研究[J].土木工程学报,2008,41(9):14-20.

[13] 李华钢,蔡 健.带约束拉杆矩形钢管混凝土短柱承载力计算[J].混凝土与水泥制品,2012(3):49-54.

[14] 陈兰响.钢骨—钢管高强混凝土构件的力学特性研究[D].大连：大连大学,2016.

[15] 蔡 健,何振强.带约束拉杆方形钢管混凝土的本构关系[J].工程力学,2006,23(10):145-150.

[16] 龙跃凌,蔡 健.带约束拉杆L形钢管混凝土短柱轴压性能的试验研究[J]．华南理工大学学报(自然科学版),2006,34(11):87-92.[17] 郑展展.双层箍筋约束混凝土圆形柱轴心受压竖向承载特性研究及有限元模拟[D].赣州:江西理工大学，2012．[18] 王 鑫.异形钢管混凝土组合柱力学性能研究[D].沈阳：沈阳建筑大学,2010.

Mechanical Performance Analysis of L Shaped Concrete-filled Square Steel Tubular Composite Columns with Restraint Bars

WU Bangrui, YANG Xiurong, FAN Cheng

(DepartmentofCivilandArchitectureEngineering,DalianUniversity,Dalian,Liaoning116622,China)

In this paper the influence of the tension constraint on the performance of composite columns is analyzed focusing on the L shaped column composed of binding bars with different types and different strength by numerical simulation, the results were compared with test results. The results show that the effect of the tension constraint on the performance improvement of the L shaped composite column could be derived from this method as well as the positive effect on the column ductility and bearing capacity. Finally the theoretical calculation method based on the linear regression analysis shows high consistency with the numerical results, and the calculation formula of the bearing capacity of the composite special-shaped columns with the constraint of the tie rod was developed.

combination column; concrete filled steel tube; finite element analysis; ductility

10.3969/j.issn.1672-1144.2017.03.032

2017-02-01

2017-03-10

吴邦睿(1988—)，男，山东邹城人，硕士研究生，研究方向为结构工程。 E-mail:wu0872@163.com

樊 成(1976—)，男，河北沧州人，博士，副教授，主要从事岩土及混凝土结构方面的研究工作。 E-mail: fan76cheng@163.com

TU398

A

1672—1144(2017)03—0157—04