中子应力谱仪样品承重台回转支承载荷分析
李 杨 吴运新 龚 海 张 宇1.中南大学机电工程学院,长沙,4100832.中南大学高性能复杂制造国家重点实验室,长沙,4100833.中南大学有色金属先进结构材料与制造协同创新中心,长沙,410083
中子应力谱仪样品承重台回转支承载荷分析
李 杨1,2,3吴运新1,2,3龚 海1,2,3张 宇1,2,3
1.中南大学机电工程学院,长沙,4100832.中南大学高性能复杂制造国家重点实验室,长沙,4100833.中南大学有色金属先进结构材料与制造协同创新中心,长沙,410083
针对中子应力谱仪样品承重台(简称“中子谱仪样品台”)旋转运动机构用三排圆柱滚子回转支承的特殊结构和受载情况,基于Hertz理论,实现了力学分析模型的建立和求解,在此基础上通过有限元法分析了中子谱仪样品台极限工况下滚子与滚道之间的接触特性,然后分析了轴向载荷、径向载荷、滚子数量对回转支承刚度的影响。研究结果表明:在中子谱仪样品台极限工况下,上排滚子与滚道的接触区域等效应力最大,为76.98 MPa,外圈滚道的最大等效应力为14.82 MPa,内圈滚道最大等效应力为11.26 MPa;刚度分别随轴向载荷、径向载荷和滚子数目的增大而增大,且均成非线性关系,当轴向载荷增至1200 kN、径向载荷增至300 kN时,轴向刚度和径向刚度增长趋势明显减慢,当上排与下排滚子数量增至170时,轴向刚度的增大趋势明显加快。研究结果为中子谱仪样品台旋转运动机构的设计提供了参考。
中子谱仪样品台;三排圆柱滚子回转支承;Hertz理论;有限元方法
0 引言
样品承重台(简称“样品台”)是中子应力谱仪(简称“中子谱仪”)的关键部件之一,为了充分发挥中子穿透距离大的优势,必须研究异形大构件各方向的内部应力分布状态,因此,要求样品台能够摆放异形大构件,实现样品的多维度运动并能灵活调整取向,精确定位。样品台旋转系统主要用来支撑整个样品台和实现样品台绕Z轴精确旋转。回转支承是旋转运动机构的重要组成部分之一,作为承载的关键部件,回转支承的精度、刚度和承载能力都直接影响到中子应力谱仪的性能。因此,探究回转支承的承载性能,提高回转支承的刚度,是实现中子应力谱仪样品台平稳运转及高精度测量的基础。

现有的解析法在对回转支承的接触特性和刚度特性分析的过程中,通常将支承的滚圈看成刚体,只考虑滚动体与滚道之间的接触变形,而没有将滚圈自身的变形计算在内,导致解析法的结果存在一定的误差。本文采用一种新的利用超单元法建立回转支承简化模型的有限元法结合解析法,对回转支承的接触特性和刚度特性进行计算分析,以弥补当前计算方法中的不足。
1 中子谱仪样品台回转支承结构
根据中子谱仪样品台旋转运动机构的空间结构和设计要求,选择型号为YRT800的三排圆柱滚子回转支承,支承结构如图1所示,各项参数见表1、表2。

图1 三排圆柱滚子回转支承Fig.1 Structure of three-row roller slewing bearing

表1 YRT800三排圆柱滚子支承外形尺寸

表2 YRT800三排圆柱滚子支承滚子参数
2 回转支承载荷及应力分布计算
2.1 上下排滚子载荷及应力分布计算
当滚子承受的载荷为p、弹性接触变形为δ时,根据“滚动轴承的分析方法”,两者存在如下关系:
p=Kδ1.1
(1)

假设外圈不发生形变,在轴向载荷Fa、径向载荷Fr以及倾覆力矩M的联合作用下,内圈产生轴向位移δa、径向位移δr及倾角位移θ。如图2所示,极轴指向径向载荷Fr方向,极角ψ在坐标中的取值范围为[-π,π]。

图2 回转支承受力变形示意图Fig.2 Slewing bearing deformation diagram
如图3所示,滚子在承受轴向载荷与倾覆力矩作用下的轴向变形为δa,角变形为θ,根据极坐标系中的几何关系,滚子的弹性变形量

(2)
式中,Dpw1为上排滚子节圆直径;Ga为上下排滚子的轴向游隙。

图3 轴向载荷及倾覆力矩作用下滚子的变形量Fig.3 Roller deformation under axial load and overturning moment
上排滚子最大弹性变形量
δumax=δa+θDpw1/2
(3)
将式(3)代入式(1)可得,任意位置角φ处的上排滚子所受的载荷

(4)

其中,εu为上排滚子载荷分布参数;Qumax为上排滚子承受的最大接触载荷。载荷作用的区域范围可由下式计算得到:
φ=arccos(1-2εu)
(5)
根据平衡原理,可得到以下力学平衡方程:
(6)
式中,Zu、Zd分别为上下排滚子的滚子数;Qdmax为下排滚子承受的最大接触载荷;Ja(ε)为轴向载荷分布积分系数;Jm(ε)为力矩载荷分布积分系数;εd为下排滚子载荷分布参数;M为倾覆力矩;Dpw2为下排滚子的节圆直径。
如图4所示,假设受载最大的上排滚子圆周角位于φ=0处,其编号为1,分别将外载荷代入,可求得滚子的变形及载荷。

图4 上排滚子数编号Fig.4 Number of top roller
轴向载荷单独作用时,上排滚子单位弧长所受的负荷线密度
ρu=Fa/(πDpw1)
(7)
在倾覆力矩单独作用下,回转支承在圆周角φ处单位弧长的线密度
(8)
当轴向载荷Fa与倾覆力矩M协同作用时,上排每个滚子所受正应力
(9)
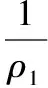
式中,ρ1、ρ2分别为两接触体的半径;ν1、ν2分别为两接触体的泊松比;E1、E2分别为两接触体的弹性模量。
由于下排滚子只承受倾覆力矩,故下排滚子在圆周角φ处单位弧长的线密度
(10)
下排滚子所受的应力
(11)
2.2 中排滚子载荷及应力分布计算
中排滚子主要承受径向载荷,由于支承的外圈固定,内圈在径向载荷的作用下会产生径向位移δrmax。根据平衡原理,可得到以下力学平衡方程:

(12)

式中,Zm为中排滚子数;Kr为径向变形常数;Gr为径向游隙;εj为载荷分布参数;Jr(ε)为径向载荷分布积分系数。
假设φx=0是受载最大滚子所在位置,其最大载荷为Qjmax,则在位置φj处滚动体所承受的载荷

(13)
其中,载荷在沿滚子分布的圆周上的作用区域范围由下式计算:
φj=arccos(1-2εj)
(14)
由回转支承的特殊结构可知,中排滚子只受到径向载荷Fr的作用,故中排滚子承受的正应力
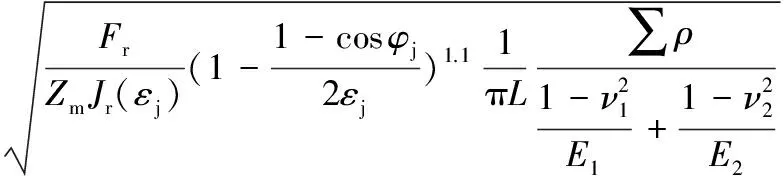
(15)
3 回转支承接触特性有限元分析
由于三排圆柱滚子回转支承的结构尺寸及圆柱滚子的数量较大,且圆柱滚子与内外圈的接触都属于非线性接触问题,故为方便研究并提高效率,本文先对模型进行了合理简化,根据平台极限工况下的外载荷(由本课题组根据动力学仿真分析得到:M=4.0 MN·mm,Fa=27.280 kN,Fr≈0),利用第2节解析法算出三排滚子所受的最大载荷,直接对滚子所受最大载荷进行分析。
3.1 有限元模型的建立
根据三排滚子回转支承整体结构的几何对称性,在上中下三排滚动体中各取一个滚子;选取Solid185与 Plane82单元;根据Hertz接触理论,使用接触半宽计算公式确定网格尺寸;根据厂家资料定义材料属性;根据回转支承实际工况施加约束,将轴向载荷与倾覆力矩共同作用下的轴向载荷均匀施加在内圈的上下表面,径向载荷均匀施加在内圈表面上。有限元模型如图5所示。

图5 有限元模型图Fig.5 Finite element model
3.2 滚子与滚道间的接触特性分析
三排滚子回转支承的上中下排滚子在结构和受载上相似,且上排滚子承受的载荷最大,最容易损坏,因此,以最具代表性的上排滚子为分析对象。上排滚子在最大协同载荷的作用下的von Mises应力、内外圈变形量的分布情况如图6~图11所示。

图6 上排滚子应力云图Fig.6 Stress nephogram of top roller

图7 上排滚子Y方向位移云图Fig.7 Displacement fringe of top roller along Y direction

图8 外圈滚道应力云图Fig.8 Stress nephogram of outer ring raceway

图9 外圈滚道Y方向位移云图Fig.9 Displacement fringe of outer ring raceway along Y direction

图10 内圈滚道应力云图Fig.10 Stress nephogram of inner ring raceway
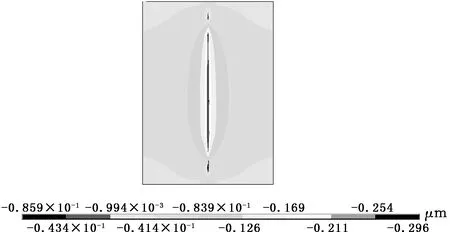
图11 内圈滚道Y方向位移云图Fig.11 Displacement fringe of inner ring raceway along Y direction
由图6~图11可知,上排滚子在轴向载荷和倾覆力矩的共同作用下,在圆柱滚子与滚道的接触区域出现了最大等效应力76.98 MPa。滚子与内圈滚道接触区域相对变形量较小,外圈滚道的最大等效应力为14.82 MPa,内圈滚道的最大等效应力为11.26 MPa。滚子与滚道接触的区域等效应力大,且滚道的应力分布呈椭圆形状,与Hertz理论一致。
由图12可知,滚子与上下滚道之间的接触区域基本相同。图12中,AB为滚子与滚道的接触直线,提取接触线上AB的10个节点,从A到B分别编号1~10,可得到接触线上节点的接触应力、等效应力及变形,如图13~图15所示。提取AO线上的12个节点,从O到A分别编号1~12,得到AO线上的等效应力如图16所示。

图12 滚子滚道接触线Fig.12 Contact line of raceway

图13 滚子接触线AB上节点的接触应力Fig.13 Contact stress of AB node of contact line

图14 滚子接触线AB上节点的Y向位移关系Fig.14 Displacement relationship of AB node of contact line along Y direction

图15 滚子接触线AB上节点的等效应力Fig.15 Equivalent stress of AB node of contact line

图16 滚子接触线AO上节点的等效应力Fig.16 Equivalent stress of AO node of contact line
由图13可知,最大接触应力出现在滚子与滚道接触的边缘位置,其接触应力与其他区域相比变化明显,这是因为滚子受载后,滚子边缘表面与滚道之间产生接触,应力迅速增大到最大值,产生边缘效应。产生边缘效应与两接触部分的弧度以及其各自倒角形状、滚子直径有关,而在建立非线性接触模型时考虑到模型收敛难的问题,上述因素都不会考虑,因此,滚子接触出现边缘效应是可以理解的。由图14可知,在接近滚子中心的区域Y向位移达到最大值,靠近接触线两端的位移较小,总体呈抛物线状。由图15可知,滚子接触线AB上等效应力分布规律与其接触应力的分布规律相似,都出现了应力边缘效应。由图16可知,在径向方向OA上,滚子的中点处等效应力最小,离接触线越近,其等效应力逐渐增大,在A点附近增长速度加快,在A点径向方向上的等效应力达到最大值。
4 回转支承刚度特性研究
4.1 轴向载荷对支承刚度的影响
回转支承上排滚子承受的轴向载荷最大,轴向变形最大,因此,利用解析法算出上排滚子所受的最大轴向载荷,对上排所受最大轴向载荷的单个滚子进行分析。
回转支承在轴向载荷Fa=2000 kN作用下,上排所受最大轴向载荷的单个滚子的应力和位移云图见图17。轴向载荷Fa分别为600 kN、1000 kN、2000 kN时,采用解析法和有限元法得到的滚子的最大应力和最大位移结果见表3。

(a)滚子在轴向载荷作用下的应力云图
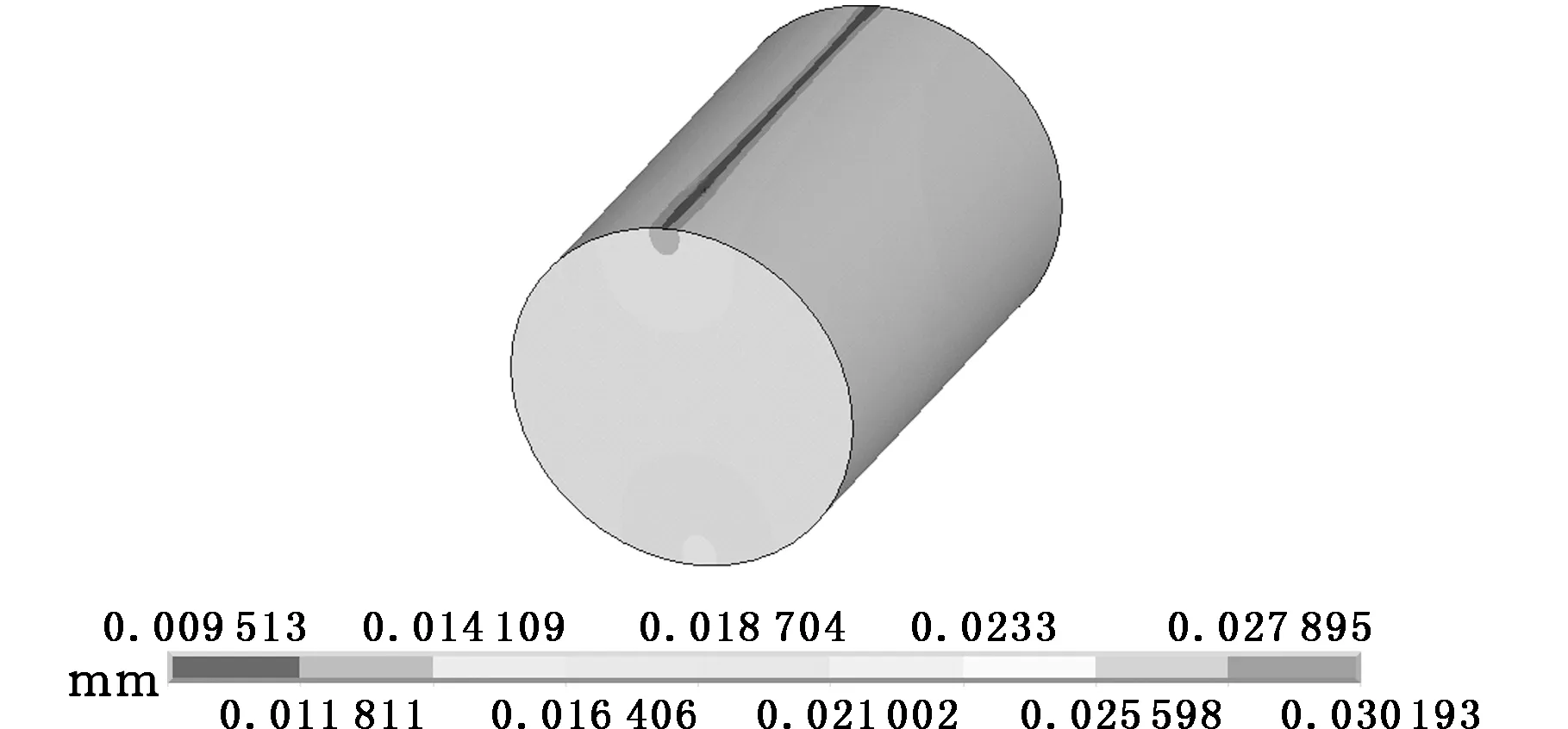
(b)滚子在轴向载荷作用下的Y向位移云图图17 Fa=2000 kN时上排滚子的应力和位移云图Fig.17 Stress nephogram and displacement fringe of top roller when Fa=2000 kN

表3 不同轴向载荷作用下解析法与有限元法结果对比Tab.3 Comparison analysis between analytical method and FEM under different axial loads
由表3可知,解析结果得到的应力值偏大,而变形值偏小,这是因为解析法中假设滚道不发生变形,从而导致解析计算出的变形量偏小。
图18所示为上排滚子在轴向载荷在0~2000 kN范围内的轴向变形和轴向刚度曲线。由图18可知,随着轴向载荷增大,轴向变形与轴向载荷之间基本成线性关系,但轴向刚度与轴向载荷之间成非线性关系,且当载荷增至1200 kN时,刚度增长趋势明显变缓。
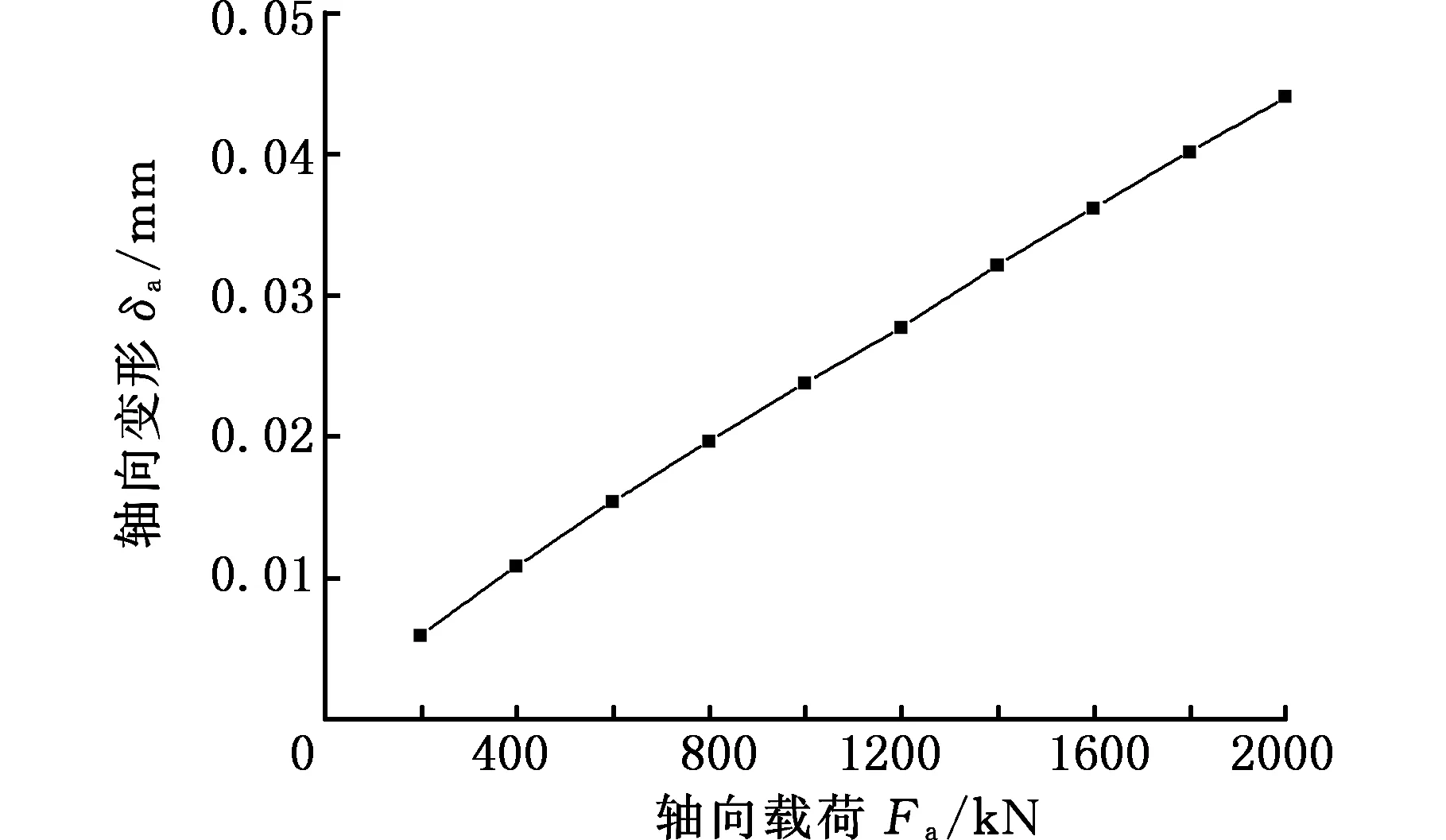
(a)滚子在轴向载荷作用下的轴向变形

(b)滚子在轴向载荷作用下的轴向刚度图18 Fa为0~2000 kN时上排滚子的变形和刚度曲线Fig.18 Deformation and stiffness curve of top roller when Fa=0~2000 kN
4.2 径向载荷对支承刚度的影响
回转支承中排滚子承受的径向载荷最大、径向变形最大,因此,利用解析法算出中排滚子所受的最大径向载荷,对中排所受最大径向载荷的单个滚子进行分析。
回转支承在径向载荷Fa=1000 kN作用下,中排所受最大载荷的单个滚子的应力和位移云图见图19。径向载荷Fr分别为100 kN、700 kN、1000 kN时,分别采用解析法和有限元法所得到的滚子的最大应力和最大位移结果见表4。
图20所示为中排滚子在径向载荷0~1000 kN范围内的径向变形和径向刚度曲线。由图20可知,随着径向载荷的增大,变形与径向载荷之间基本上成线性关系,但径向刚度与径向载荷之间成非线性关系,且当径向载荷增至300 kN时,刚度的增长趋势明显变缓。

(a)滚子在径向载荷作用下的应力云图
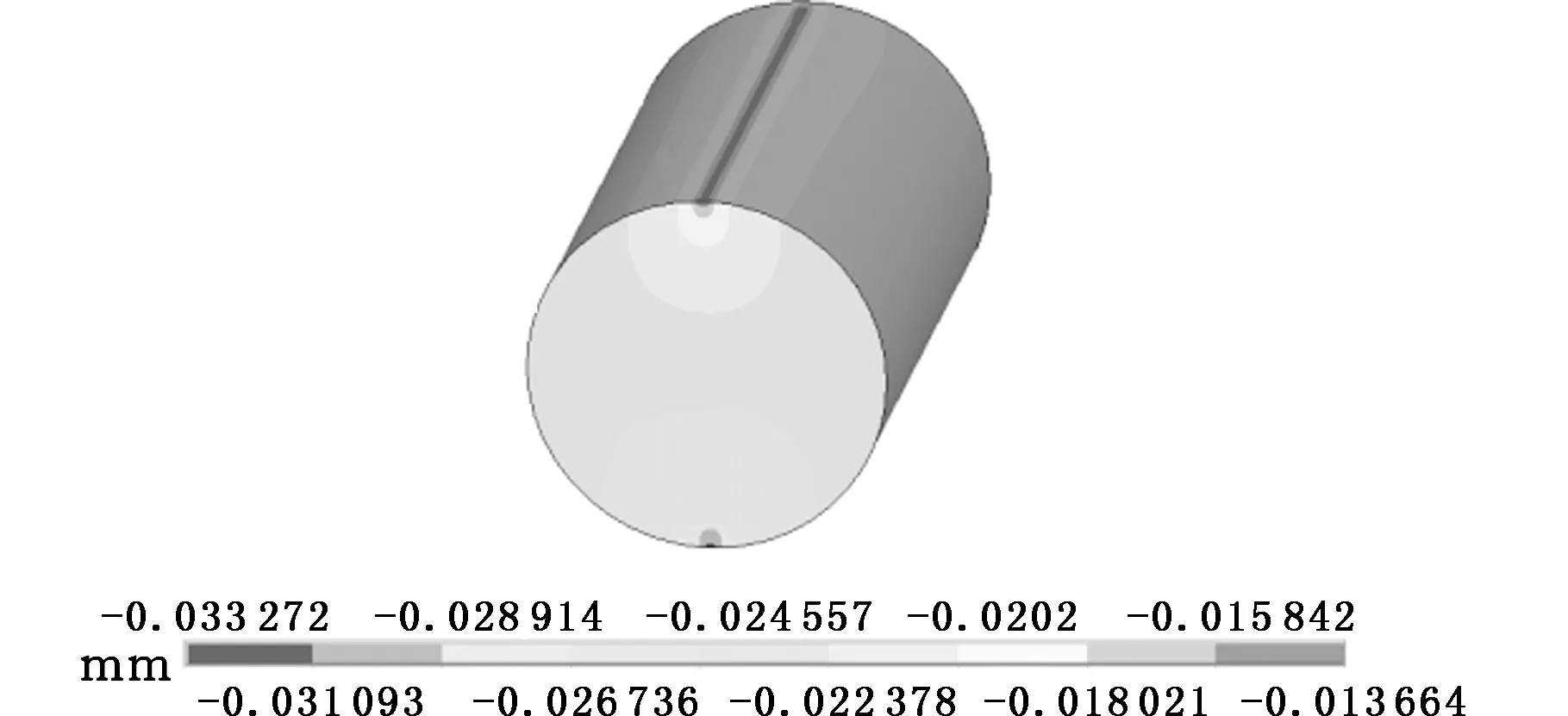
(b)滚子在径向载荷作用下的Y向位移云图图19 Fa=1000 kN时中排滚子的应力和位移云图Fig.19 Stress nephogram and displacement fringe of center roller when Fa=1000 kN
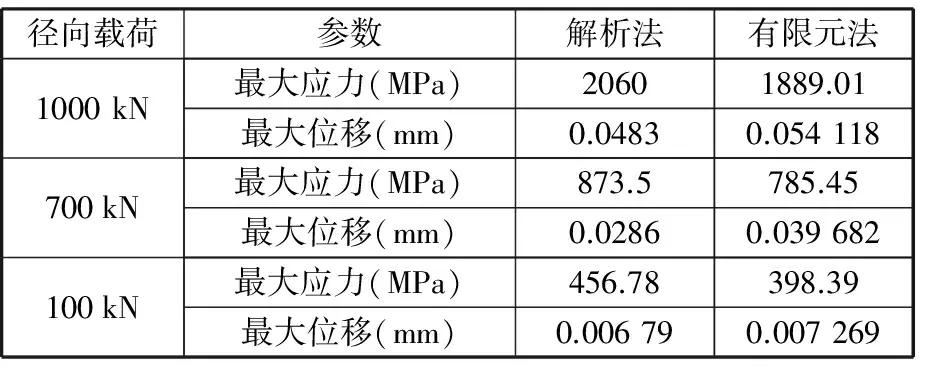
表4 不同径向载荷作用下解析法与有限元法结果对比
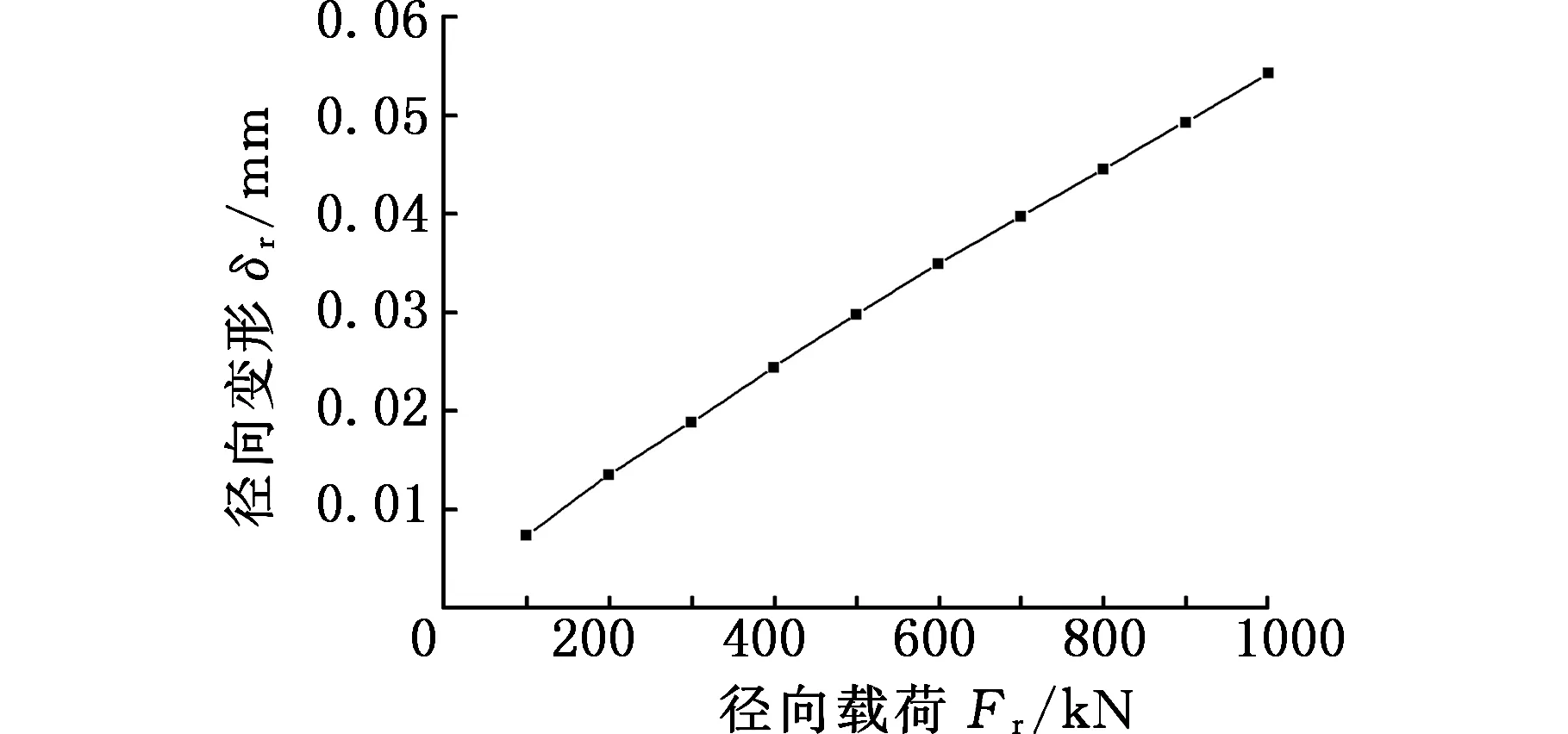
(a)滚子在径向载荷作用下的径向变形
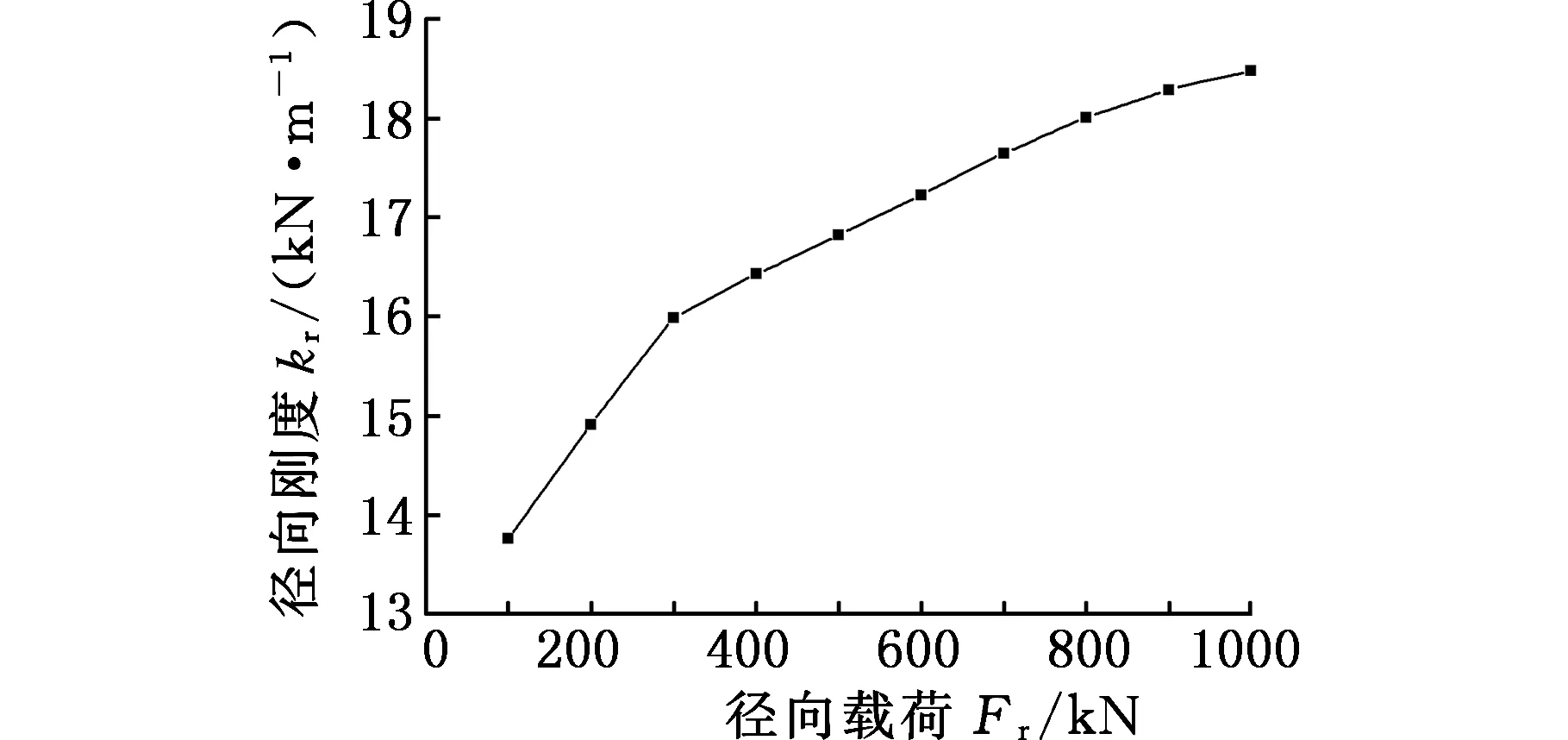
(b)滚子在径向载荷作用下的径向刚度图20 Fr为0~1000 kN时中排滚子的变形和刚度曲线Fig.20 Deformation and stiffness curve of center roller when Fr =0~1000 kN
4.3 滚动体直径与数量对支承刚度的影响
当滚动体的数量改变时,支承的刚度也会受到影响,但在实际装配支承的过程中,滚动体越多装配越困难,而且影响支承启动的灵活性。由于支承在工作中主要承受轴向力,支承对轴向刚度要求高,故本节仅研究滚动体直径与数量对支承轴向刚度的影响。
保持三排滚子支承结构中的其他参数不改变,只改变上排与下排滚子的数量。由三排滚子回转支承的结构特性可知,滚子组节圆直径Dw、滚子直径Dpw及滚子数Z之间存在以下关系:
Z=πDpw/(KzDw)
(16)
其中,Kz取1.1~1.3,上排与下排滚子数分别取150、160、170、180、190,中排滚子数目保持不变,施加1000 kN的轴向载荷,利用解析法算出上排滚子所受的最大轴向载荷,对上排所受最大轴向载荷的单个滚子进行分析,则滚动体的数量对上排所受最大轴向载荷的单个滚子轴向刚度影响曲线如图21所示。由图可知,随着滚子数目的增加,轴向刚度与滚子数目之间成非线性关系,且当滚子数量增至170时,刚度的增长趋势加快。

图21 滚子数量与轴向刚度之间的关系Fig.21 Relationship between the number of roller and axial stiffness
5 结论
(1)中子谱仪样品台极限工况下,上排滚子在轴向载荷和倾覆力矩的共同作用下,滚子与滚道的接触区域等效应力最大,为76.98 MPa。外圈滚道的最大等效应力为14.82 MPa,内圈滚道最大等效应力为11.26 MPa;滚子与内圈滚道接触区域相对变形量比滚子与外圈滚道接触区域相对变形量小。
(2) 中子谱仪样品台极限工况下,上排滚子在轴向载荷和倾覆力矩的共同作用下,最大接触应力出现在滚子与滚道接触的边缘位置;靠近接触线两端的位移较小,接近滚子中心区域位移达到最大值,总体呈抛物线状;滚子接触线上接触应力的分布规律与等效应力分布规律相似,都出现了应力边缘效应;径向方向上,滚子中点处等效应力最小,离接触线越近等效应力越大,在接触线处等效应力达到最大值。
(3) 轴向变形和径向变形分别随着轴向载荷和径向载荷的增大而增大且基本成线性关系,而刚度分别随轴向载荷、径向载荷和滚子数目的增大而增大,且均成非线性关系。当轴向载荷增至1200 kN,径向载荷增至300 kN时,轴向刚度和径向刚度增长趋势明显变慢;当上排与下排滚子数量增至170时,轴向刚度的增长趋势加快。
[1] 汪洪,李颖,田仁. 多排滚子转盘轴承承载能力的计算[J]. 轴承,2012(2):8-11. WANG Hong,LI Ying,TIAN Ren. Calculation of Load Capacity for Multi-row Roller Slewing Bearings[J]. Bearing, 2012(2):8-11.
[2] 黄浩,张鹏顺,温建民. 高速圆柱滚子轴承的刚度研究[J]. 中国机械工程, 2001,12(11):44-46. HUANG Hao,ZHANG Pengshun,WEN Jianmin. Study of Stiffness of High-speed Cylindrical Roller Bearing[J]. China Mechanical Engineering, 2001,12(11):44-46.
[3] 陈家庆,张富辉,周永新. 线接触问题的弹性趋近量与滚子轴承的载荷分布[J]. 机械设计与制造, 2003(3):40-42. CHEN Jiaqing,ZHANG Fuhui,ZHOU Yongxin. The Elastic Approach for Linear Contact Problem and Roller Bearing’s Load Distribution[J]. Machinery Design & Manufacture, 2003(3):40-42.
[4] 姜笑颖,张钢,支汗立,等. 特种推进器用三排圆柱滚子式转盘轴承的负荷分析[J]. 机械制造与自动化, 2015,44(6): 74-78. JIANG Xiaoying,ZHANG Gang,ZHI Hanli,et al. Load Distribution Analysis of Three-row Cylindrical Roller Slewing Bearing for Special Propeller[J]. Machine Building & Automation, 2015,44(6):74-78.
[5] 张建. 基于柔性支撑的转盘轴承性能及结构参数研究[D]. 大连:大连理工大学,2015. ZHANG Jian. Research on Performance and Structural Parameters of Slewing Bearing with Flexible Supporting Structures[D].Dalian :Dalian University of Technology,2015.
[6] 龚国伟.风电机组法兰螺栓连接建模与仿真技术研究[D]. 重庆:重庆大学,2014. GONG Guowei. Modeling and Simulink Research about the Flange Bolts Connection of Wind Turbine[D]. Chongqing :Chongqing University,2014.
[8] KANIA L. Modelling of Rollers in Calculation of Slewing Bearing with the Use of Finite Elements[J].Mechanism and Machine Theory,2006,41(11):1359-1376.
[9] GÖNCZ P, ULBIN M, GLODEŽ S. Computational Assessment of the Allowable Static Contact Loading of a Roller-slewing Bearing’s Case-hardened Raceway[J]. International Journal of Mechanical Sciences,2015,S94-95:174-184.
[10] AGUIRREBEITIA J, ABASOLO M, AVILÉS R, et al. Theoretical Calculation of General Static Load-carrying Capacity for the Design and Selection of Three Row Roller Slewing Bearings[J]. Mechanism and Machine Theory,2012,48(1):52-61.
(编辑 陈 勇)
Load Analysis of Neutron Spectrometer Sample Table Rotary Bearing
LI Yang1,2,3WU Yunxin1,2,3GONG Hai1,2,3ZHANG Yu1,2,3
1.College of Mechanical and Electrical Engineering, Central South University, Changsha,410083 2.State Key Laboratory of High Performance Complex Manufacturing, Central South University,Changsha,410083 3.Nonferrous Metal Oriented Advenced Structural Materials and Manufacturing Cooperative Innovation Center,Central South University,Changsha,410083
According to the three-row roller slewing bearing structure characteristics and load characteristics, the establishment and solution of the mechanics analysis model were achieved by using Hertz contact theory. The contact characteristics of slewing bearing between the roller and the raceway were analyzed by using FEM on the basis of mechanics analysis model, then the effects of axial loads, radial loads and roller numbers on the slewing bearing stiffnesses were analyzed. The results show that under the extreme conditions the equivalent stress of contact area of upside roller and raceway is largest, which is as 76.98 MPa, the maximum equivalent stress of outer ring raceway is as 14.82 MPa, the maximum equivalent stress of inner ring raceway is as 11.26 MPa. Stiffnesses increase with increasing of axial loads, radial loads and roller numbers respectively and the relationship among them are nonlinear, when the axial loads increase to 1200 kN and radial loads increase to 300 kN, axial stiffness and radial stiffness increasing rates slow down significantly, when the roller numbers increase to 170, the axial stiffness increasing rates speed up significantly. The study may provide useful references for neutron spectrometer sample table rotating motion mechanism structure design.
neutron spectrometer sample table; three-row roller slewing bearing; Hertz theory; finite element method(FEM)
2016-06-12
国家自然科学基金资助项目(51327902);高性能复杂制造国家重点实验室自主研究课题(2014bcxjj06)
TH133
10.3969/j.issn.1004-132X.2017.12.008
李 杨,男,1982年生。中南大学机电工程学院博士研究生。研究方向为机械设计及理论。吴运新(通信作者),男,1963年生。中南大学机电工程学院教授、博士研究生导师。E-mail:wuyunxin@csu.edu.cn。龚 海,男,1982年生。中南大学机电工程学院讲师、博士。张 宇,男,1990年生。中南大学机电工程学院硕士研究生。

