Delta机器人综合位置误差研究及其耦合特性分析

郑坤明， 张秋菊

(1.江南大学机械工程学院 无锡，214122) (2.江苏省食品先进制造装备技术重点实验室 无锡，214122)



Delta机器人综合位置误差研究及其耦合特性分析

郑坤明1,2， 张秋菊1,2

(1.江南大学机械工程学院 无锡，214122) (2.江苏省食品先进制造装备技术重点实验室 无锡，214122)

以Delta机器人为分析对象，研究了动平台的位置误差模型，并对误差源的耦合特性进行了分析。首先，利用从动臂的位置特性，依据几何空间矢量法，建立了Delta机器人机构误差模型；其次，以数理统计与空间矢量原理为基础，推导出Delta机器人关节间隙误差模型；然后，基于空间有限元理论，在建立系统弹性动力学模型的基础上建立了其柔性误差模型；综合考虑这3种误差源，建立了Delta机器人综合位置误差模型；最后，利用Adams与Workbench联合仿真、Matlab数值计算和FARO激光跟踪仪的现场试验验证了位置误差模型的正确性，并对误差源的耦合特性进行了分析，阐述了方向位置误差与坐标轴方位之间的关系。结果表明，影响Delta机器人动平台位置误差的各个误差源间并不是简单的叠加，而是具有明显的耦合特性，并且动平台方向位置误差会随着坐标轴方位的变化而变化。

Delta机器人； 机构误差模型； 间隙误差模型； 柔性误差模型； 综合位置误差； 耦合特性

引 言

末端执行器的位置精度是评价并联机器人性能的重要指标，但是目前尚未得到较为完善的解决[1-4]。随着工业水平的提高，并联机器人向着高速、轻量化方向发展，影响其末端执行器位置精度的因素越来越复杂。目前，国内外学者对并联机器人的位置精度与补偿方法[5]进行了大量的研究。Chen等[6]通过建立一种四轴式Delta机器人误差模型，对影响末端执行器位置精度的机构误差源进行了灵敏度分析。文献[7-13]研究了关节间隙对并联机构位置误差的影响。Chen等[14]系统阐述了关节间隙对并联机器人位置误差的不确定性。Frisoli等[15]基于螺旋理论对并联机构进行了误差分析。Jokin等[16]研究了静刚度对6-RUS并联操作器位置精度的影响。Amir等[17]将动平台视为柔性体，研究了系统刚度对3-PSP并联机器人精度的影响。Sébastien等[18-19]对一种3T1R并联机器人进行了精度分析。但是，以上关于并联机器人误差研究还主要集中在各个单独的误差源领域，即假设末端执行器的位置精度仅受到单一误差源的影响，没有全面考虑误差源综合效应，忽略各个误差源在运行过程中的耦合特性。经过前期的研究可知，全面考虑误差源并对其进行耦合特性分析，对改善控制策略及提高并联机器人末端执行器的位置精度具有重要的意义。

基于以上认识，笔者以Delta机器人为研究对象，全面考虑影响动平台位置精度的误差来源，分别建立了Delta机器人机构误差模型、关节间隙误差模型与柔性误差模型。在此基础上，对以上误差源进行了综合研究，通过软件仿真、数值计算与现场试验对其进行了耦合特性分析，所得出的耦合指标为进一步优化控制策略、提高动平台的位置精度提供了新的途径与重要依据。最后说明了各个方向位置误差随系统坐标系坐标轴方位变化的关系。

1 Delta机器人系统描述与坐标系的建立

Delta机器人的结构示意图如图1所示，系统由静平台A1A2A3、动平台C1C2C3、主动臂AiBi、从动臂BiCi(i=1,2,3)组成。主动臂与静平台之间用转动关节连接，主动臂与从动臂、从动臂与动平台之间以虎克铰的形式连接，为了方便加工装配与理论分析，这里虎克铰由两个轴线相互垂直的转动关节代替。在静、动平台的中心处分别建立如图1所示的系统坐标系O-XYZ与局部坐标系p-xyz。设动平台中心p相对于坐标系O-XYZ的坐标为(x,y,z)，主动臂的分布角为θi，αi为主动臂输入角度，la和lb分别为主、从动臂的长度，R和r分别为静、动平台外接圆半径。

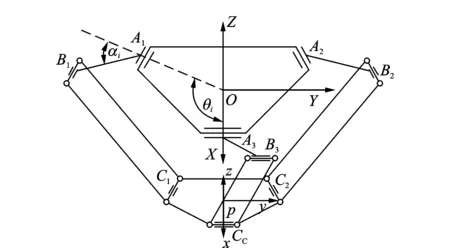
图1 Delta机器人的结构示意图Fig.1 Schematic diagram of Delta robot

2 Delta机器人机构误差模型

机构误差是产生Delta机器人末端执行器——动平台位置误差的重要来源，本部分将利用从动臂连接主动臂输入端与动平台输出端的位置特性，以从动臂为中间媒介，推导其在三维空间中的位置矢量，依据几何空间矢量法，建立Delta机器人机构误差模型。

这里，将Delta机器人的所有杆件视为刚性体，忽略其弹性变形，仅考虑它们的加工装配误差即机构误差。为了便于分析，将3组平行四边形形式的从动臂简化为3根刚性连杆BiCi，如图2所示。

图2 等效从动臂Fig.2 Equivalent driven arm

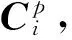
(1)

设ubi为Ci指向Bi的单位矢量，则对于第i条支链的从动臂有lbiubi=Ci-Bi，即

(2)

对式(2)两端求微分得

(3)

(4)

等式(4)左边两项具体表达形式如下，左边第1项为

由机器人的微分关系[20]知：dubi=Δubiubi，其中

左边第2项为

(5)

(6)

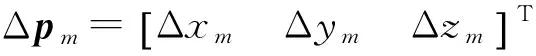
考虑到Delta机器人具有3条支链，将式(6)写成如下形式

(7)

令

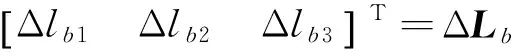
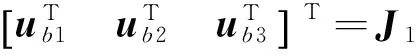
又因为

Δrsinθi+rΔθdicosθi+ΔymΔzm]T

将含有动平台的位置误差项分离出来可得

则

令

将式(7)整理，可进一步表示为

ΔLb=2J1Δpm+J2ΔV

(8)

将式(8)整理为动平台位置误差的显式形式

Δpm=JmΔem

(9)

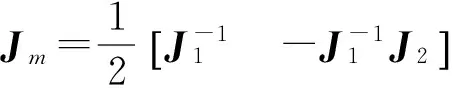
至此，建立了Delta机器人机构误差模型。其中：Jm，Δem分别为机构误差传递矩阵与机构误差输入矩阵。

3 Delta机器人间隙误差模型

Delta机器人由多根杆件通过转动关节相连接，由于加工和装配过程中存在误差，转动关节处会不可避免地出现间隙，关节间隙对动平台的位置精度有着不可忽视的影响。关节间隙随机器人运动状态变化而变化，对动平台位置精度的影响具有不确定性[21]。基于此，本部分将以数理统计与空间矢量原理为基础，研究关节间隙对Delta机器人动平台位置精度的影响。为便于分析，这里挑选Delta机器人的任一支链作为研究对象，即i为1,2,3中的任一常数。

3.1 关节间隙模型

将关节间隙矢量分解在径向与轴向方向上，可得径向间隙矢量Cirj与轴向间隙矢量Ciaj。Cirj与Ciaj随着Delta机器人运动状态的改变在关节径向与轴向随机跳动，其二维投影示意图如图3所示。其中：Ci1j，Ci2j分别表示关节间隙的外圆圆心与内圆圆心；eij为关节间隙外圆柱左端面的圆心点。

图3 关节间隙的投影示意图Fig.3 Schematic diagram of the projection of the joint clearance

为反映关节间隙矢量随机器人运动状态变化的随机性与不确定性，需根据数理统计知识在直角坐标系中建立其概率密度函数。对径向间隙矢量Cirj，设坐标系原点为间隙外圆圆心Ci1j，并假定其分布为正态分布，可得其概率密度firj(xirj,yirj)为

firj(xirj,yirj)=

(10)

对于轴向间隙矢量Ciaj，设其坐标系原点为关节间隙外圆柱左端面的圆心点eij，其概率密度fiaj(xiaj)为

(11)

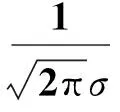
至此，建立了一般转动关节间隙变量模型。

3.2 Delta机器人动平台误差分布函数

取出Delta机器人的一条支链进行分析，忽略除关节间隙之外的误差源，可得支链结构示意图如图4所示。

图4 单支链关节间隙模型Fig.4 The joint clearance model of single chain

由图4所示，关节Ai，Bi，Ci在同一平面上，将其命名为平面1；将关节bi1，bi2，ci1，ci2所在的平面命名为平面2。将Ai，Bi，Ci，bi1，bi2，ci1和ci2依次标为1～7号关节，其径、轴向关节间隙矢量分别为Cirj和Ciaj(j=1，2，…，7)。pic为动平台中心点所在的实际位置，pic0表示动平台中心点的理想位置。这样，在不考虑其他类型误差的情况下，可将Delta机器人支链中的关节分解到两组平面内，进行关节间隙的分析，然后再将分析的结果矢量进行空间合成。依据支链的结构特点，可得如下的矢量关系式[10]

(12)

由式(10)、式(12)可得到由径向间隙引起的动平台位置误差的概率密度函数

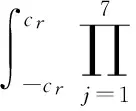
(13)

其中：cr为径向间隙的最大值。

根据式(11)、式(12)可得，由轴向间隙引起的动平台位置误差的概率密度函数为

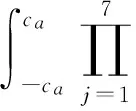
(14)

其中：ca为径向间隙的最大值。

根据式(13)、式(14)可得，由关节间隙引起的动平台位置误差分布函数为

(15)

其中：S为动平台位置误差分布区域(为了计算分析的方便，通常假定S为空间球体区域)

由以上分析可知，当给定关节间隙的具体值时，可求得动平台中心点出现某个位置误差值的概率，即由关节间隙引起的动平台中心点的位置误差是一个不确定的值，具有随机性。

3.3 Delta机器人关节间隙误差模型

利用D-H方法建立Delta机器人关节间隙与动平台位置误差之间的映射关系[12]

Δpc=JcΔec

(16)

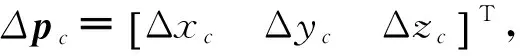
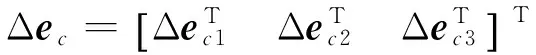
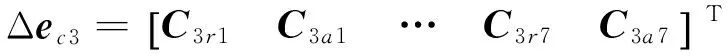
根据3.1与3.2节的分析，并结合式(15)和式(16)，将由关节间隙引起的动平台的位置误差进行综合，可得到动平台位置误差出现某个具体数值的概率。

当给定关节间隙的具体值时，动平台中心点位置误差出现某一数值是一个概率事件，为便于分析，取Δpc作为动平台中心点位置误差。至此，建立了Delta机器人关节间隙的误差模型。

4 Delta机器人柔性误差模型

为提高Delta机器人的运行效率，其杆件越来越轻质化，在高速、重载工况下，这将会引起杆件的弹性变形[22]，降低动平台的位置精度。本部分将在建立Delta机器人弹性动力学模型的基础上，建立其柔性误差模型，分析杆件弹性变形对动平台位置误差的影响。

4.1 支链弹性动力学模型

4.1.1 单元坐标系中支链弹性动力学方程

选择圆形截面、环形截面空间梁单元作为主、从动臂基本梁单元模型。因静、动平台与转动关节的刚度远大于主、从动臂的刚度，将静、动平台与转动关节看做刚性元件，忽略其运动过程中的弹性变形；主、从动臂视为柔性元件，考虑其在运动过程中的弹性变形。

将主动臂视为空间悬臂梁，则节点Ai的弹性位移和转角位移均为零。因为绕转动副轴线方向的曲率为零，则主动臂的广义坐标为10个，从动臂的广义坐标为14个。主、从动臂的空间梁单元有限元模型如图5，6所示。

根据空间梁单元动力学方程得主、从动臂的弹性动力学方程

(17)

(18)

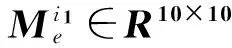
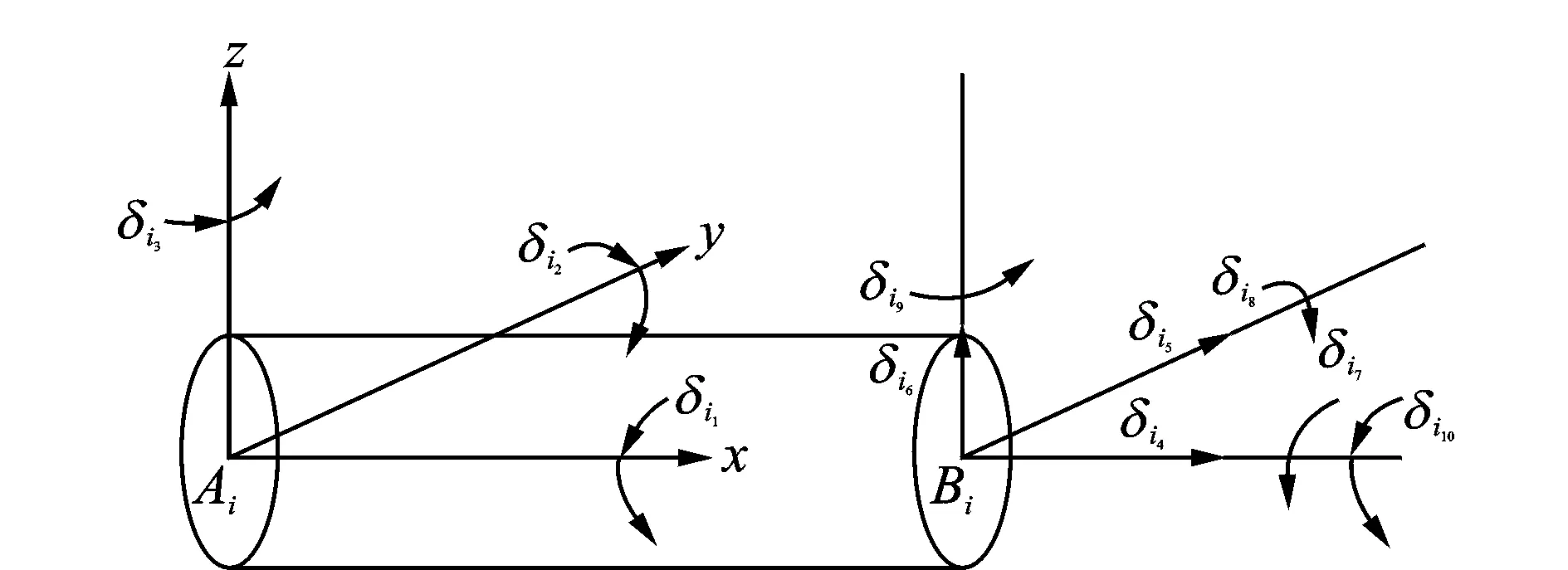
图5 主动臂空间梁单元有限元模型Fig.5 Space finite element model of active arm

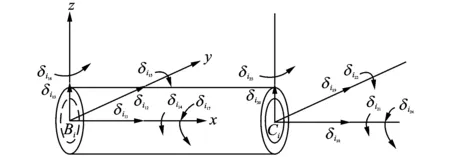
图6 从动臂空间梁单元有限元模型Fig.6 Space finite element model of driven arm

将式(17)、式(18)组合可得支链的动力学方程

(19)

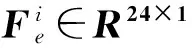
4.1.2 系统坐标系中支链弹性动力学方程

以下分析中以支链3为例，系统坐标系中支链的有限元模型如图7所示。其中：φi为主动臂AiBi与从动臂平面bi1bi2ci1ci2的夹角；BiDi为主动臂的延长线在从动臂平面上的投影；ψi为从动臂横轴bi1bi2与BiCi的夹角；φi为从动臂与BiDi的夹角；φi，ψi和φi都是随Delta机器人的位形变化的角度值。可对Delta机器人进行运动学分析得到它们的变化规律

图7 系统坐标中支链的有限元模型Fig.7 Branched chain’s finite element model in system coordinates

(20)

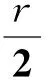
(21)

则系统坐标系O-XYZ到主动臂单元坐标系Ai-xyz的姿态变换矩阵为

(22)

系统坐标系O-XYZ到从动臂单元坐标系Bi-xyz的姿态变换矩阵为

(23)

其中：Ri211=cosφi(sinφisinαi+cosφicosαicosθi+sinφicosαisinθi)；Ri212=sinφicosθi-cosφicosφisinθi；Ri213=sinφisinαisinθi-cosφi(sinφisinαi-cosφicosθisinαi)；Ri221=cosφicosαisinθi-sinφi×(sinφisinαi+cosφicosαicosθi)；Ri222=cosφicosθi+cosφisinφisinθi；Ri223=sinφisinφicosαi-cosφicosθisinαi+cosφisinαisinθi；Ri231=sinφicosαicosθi-cosφisinαi；Ri232=sinφisinθi；Ri233=cosφicosαi+sinφicosθisinαi。

由式(22)、式(23)可得支链i的单元广义坐标与系统广义坐标之间的转换关系为

δi=BiUi

(24)

其中：Bi∈R24×21为支链i的单元广义坐标与系统广义坐标之间的姿态转换矩阵。

将式(24)代入式(19)，得到支链i在系统坐标下的弹性动力学方程为

(25)

4.2 Delta机器人系统弹性动力学模型

4.2.1 系统弹性动力学方程

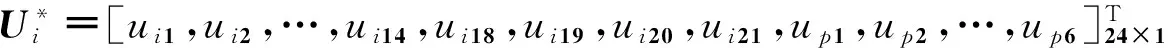
(26)

将式(26)代入式(25)得

(27)

通过运动学约束条件与式(27)可得Delta机器人整机系统的刚柔混合弹性动力学方程

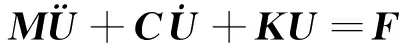
(28)

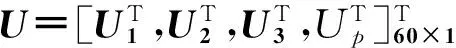
4.2.2 Delta机器人柔性误差模型

对式(36)变形可得

(29)

5 Delta机器人综合位置误差仿真与实验及其耦合特性分析

Delta机器人动平台的综合位置误差是受机构误差、间隙误差与柔性误差共同影响的。由于运行过程中各个支链结构的耦合性，使得动平台的综合位置误差不仅是以上3种类型误差源的简单叠加。本部分将结合机构误差、间隙误差与柔性误差模型，对动平台的综合位置误差进行研究，并通过软件仿真、数值计算与现场试验对其耦合特性进行分析。

5.1 Delta机器人综合位置误差

经分析，得到包含机构误差、间隙误差与柔性误差的综合弹性动力学模型

(30)

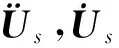
对式(30)变形得

(31)

同样地，利用Newmark法对综合弹性位移进行求解，取出列阵Us第55，56，57行，得包含机构误差、间隙误差与柔性误差在内的动平台的综合位置误差

5.2 Delta机器人综合位置误差仿真与试验

取动平台中心点p=(x,y,z)的运动轨迹为

(32)

已知系统参数如下：主动臂与从动臂的材质均为铝合金，密度为ρ=2 700 kg/m3，拉压弹性模量E=7.0×1010N/m2，剪切弹性模量G=2.65×1010N/m2；la=0.2 m，lb=0.5 m，R=0.15 m，r=0.085 m，圆形截面主动臂半径D1=0.025 m，环形截面的从动臂外径D2=0.016 m，内径d=0.014 m；动平台质量mp=1.087 kg；λ1=2.0×10-3，λ2=3.0×10-4。Delta机器人的机构误差如表1所示，各个关节的最大间隙如表2所示，这里3条支链对应关节的最大间隙相同。

表1 Delta机器人的机构误差

表2 Delta机器人的最大关节间隙

Tab.2 The maximum joint clearance of Delta robot

mm

为了分别验证前述所建机构误差模型、间隙误差模型与柔性误差模型的正确性，首先，根据此前分析，在Matlab中编程运算，得到Delta机器人分别仅具有机构误差、间隙误差与柔性误差时动平台的位置误差的数值计算结果；然后，在creo2.0中建立Delta机器人简化三维模型，将其分别导入Adams与Ansys/ Workbench。在Adams中添加驱动和约束，运用设计变量法在Delta机器人模型上分别加入机构误差与间隙误差，得到当模型仅具有机构误差与间隙误差时动平台位置误差的软件仿真结果。在Workbench中，将Delta机器人的主动臂与从动臂进行柔性化，如图8所示。利用柔性化后的杆件代替Adams中的刚性杆件，得到当Delta机器人模型仅具有柔性误差时动平台的位置误差的软件仿真结果，将数值计算与软件仿真结果相对比。

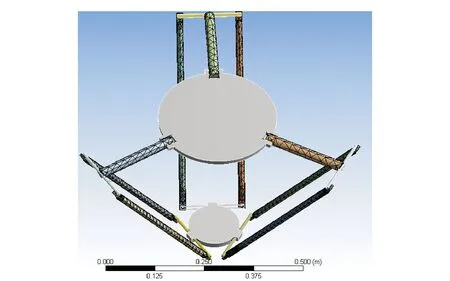
图8 Delta机器人的杆件柔性化Fig.8 Rod flexible of Delta robot

为了证明Delta机器人的机构误差、间隙误差与柔性误差对动平台位置误差的影响并不是简单的叠加作用，而是具有较强的耦合特性，将机构误差、间隙误差与柔性误差一起施加到Adams中的Delta机器人模型上，如图9所示，得到具有全部误差源的动平台软件仿真综合位置误差。

图9 Delta机器人在Adams中的模型Fig.9 Delta robot′s model in Adams

根据5.1节中求得的综合误差方程，利用Newmark法在Matlab中数值求解，得到动平台数值计算综合位置误差。

根据结构参数，加工装配出Delta机器人物理样机。利用FARO Vantage激光跟踪仪作为测量动平台综合位置误差的仪器，如图10所示。对激光跟踪仪测得的动平台的实际位置数据进行导出处理，得到动平台实际综合位置误差。

图10 FARO激光跟踪仪测量物理样机动平台运动轨迹Fig.10 FARO laser tracker measuring moving platform trajectory of the physical prototype

将动平台综合位置误差的软件仿真结果、数值计算结果与试验结果导入到Matlab中，并与直接叠加的动平台位置误差相比较，如图11～图13所示。

图11 x方向位置误差Fig.11 The position error of x axis direction

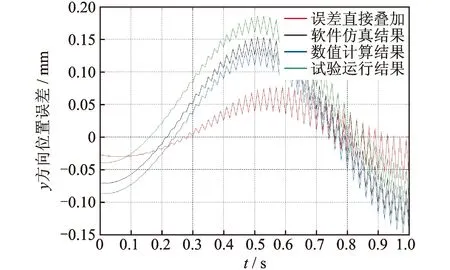
图12 y方向位置误差Fig.12 The position error of y axis direction

图13 z方向位置误差Fig.13 The position error of z axis direction

由图11～图13可以看出，软件仿真、数值计算结果与试验运行结果的曲线虽然大体吻合，但还是具有一定的偏离，分析其原因主要如下：

1) 为了建模与求解的方便，对Delta机器人在Adams中的多体动力学模型部分零部件进行了简化，因此其与实际物理样机的结构形式并不完全一致；

2) 在对系统的弹性动力学方程进行分析时，使用了Newmark法对其进行求解，结果存在一定的数值计算误差；

3) 物理样机搭建在由型材组成的安装框架上，虽然安装框架已由地脚螺栓固定在地面上，但是在运行过程中，型材的轻微抖动会对试验结果产生一定的影响。

5.3 综合位置误差耦合特性分析

由图11～图13可以看出，动平台综合位置误差的软件仿真结果、数值计算结果与试验结果大致吻合，但与直接叠加的位置误差有着明显的区别。在验证了所建综合位置误差模型正确的同时，也说明影响Delta机器人动平台的位置误差的误差源具有较明显的耦合特性。

为定量描述各个误差源对动平台位置误差的耦合作用，这里定义误差耦合指标。根据式(30)、式(31)可知，Delta机器人综合弹性动力学刚度矩阵Ks能唯一表达各个误差源耦合关系。定义λs[8]为各个误差源的耦合指标

(33)

其中：σk为矩阵Ks的奇异值；λs描述了各个误差源对动平台位置误差的耦合量化关系。

图14所示为动平台按照轨迹式(32)运行时λs随时间的变化规律。

图14 耦合指标随时间的变化规律Fig.14 Change regulation of the coupling index with time

耦合指标反映了各个误差源对动平台位置误差的耦合效应。由图14可看出，Delta机器人的耦合指标并不像文献[8]描述的那样具有明显的余弦规律，这是因为本研究的Delta机器人属于并联机器人，运动过程中各个支链之间存在很强的耦合作用，导致耦合指标没有呈现很明显的规律性。

根据工作任务得到耦合指标λs随动平台工作轨迹的变化规律，这对改善系统的控制策略和提高动平台的运动精度具有非常重要的意义。例如，在位置误差较大处可利用各个误差源的耦合效应对其进行控制和消减，也可作为尺度综合的优化目标，同时，可为待加工零件制定合适的公差提供指导。

另外发现，在整个运行过程中， 动平台y方向的位置误差平均值大于x的z方向的位置误差平均值，为了分析其原因，设y轴与OA3的夹角为β，如图15所示。

图15 改变β值Fig.15 Chang value β

令y轴绕z轴旋转，变化β的值，改变原始系统坐标系O-XYZ的y坐标轴方位，令β分别为60°，45°，30°，15°和0°。在Adams中做仿真分析，发现y方向的位置误差平均值随着β角的减小而减小，当β=0°时，y方向位置误差曲线几乎与原始系统坐标系x方向的位置误差曲线重合。究其原因主要为：

1) 动、静平台各有3个中心对称的铰链点Ai，两两铰链点之间相当于组成一个简支梁，而越靠近简支梁的中间点部位，刚度逐渐减小，弹性位移逐渐增加；

2) 在上面所述的简支梁中间点附近的位置误差受两个铰链支反力的共同作用，在动平台运行过程中，简支梁中间点附近会产生位置误差的耦合与叠加，从而导致位置误差的增加。

6 结 论

1) 利用从动臂的位置特性，导出其在三维空间中的位置矢量，建立了Delta机器人机构误差模型。以数理统计与空间矢量原理为基础，研究关节间隙对动平台位置精度影响的随机性，推导出Delta机器人间隙误差模型。利用有限元理论，充分考虑主、从动臂的空间运动特性，在建立Delta机器人弹性动力学模型的基础上，建立了其柔性误差模型。

2) 将柔性误差模型按照刚性、柔性及刚柔耦合部分的原则进行分解，利用由于机构误差与关节间隙的存在导致的刚体广义力变化，将这3个误差源进行综合，推导出Delta机器人综合位置误差模型。

3) 利用软件仿真、数值计算与现场试验验证了位置误差模型的正确性，同时说明了影响Delta机器人动平台位置精度的各种误差源具有较明显的耦合特性。通过定义误差源的耦合指标，为进一步优化控制策略，提高动平台的位置精度提供了新的途径。通过对系统坐标系进行变换，说明各个方向位置误差的变化与系统坐标系的坐标轴方位具有密切的关系。

[1] Tan Dapeng, Ji Shiming, Jin Mingsgeng. Intelligent computer-aided instruction modeling and a method to optimize study strategies for parallel robot instruction[J]. IEEE Transactions Education, 2013,56(3): 268-273.

[2] Kunt E D, Naskali A T, Sabanovic A. Miniaturized modular manipulator design for high precision assembly and manipulation tasks[C]∥ The 12th IEEE International Workshop on Advanced Motion Control. Sarajevo:B & H,2012.

[3] Yu Dayong. Parallel robots pose accuracy compensation using back propagation network[J]. International Journal of the Physical Science, 2011,6(21): 5005-5011.

[4] Brogardh T. Present and future robot control development—an industrial perspective[J]. Annual Reviews in Control, 2006, 31(1): 69-79.

[5] 谢平，杜义浩，田培涛，等.一种并联机器人误差综合补偿方法[J].机械工程学报，2012,48(9):44-49.

Xie Ping, Du Yihao, Tian Peitao, et al. Parallel robot error comprehensive compensation method[J]. Journal of Mechanical Engineering, 2012,48(9):44-49. (in Chinese)

[6] Chen Yuzhen，Xie Fugui，Liu Xinjun, et al. Error modeling and sensitivity analysis of a parallel robot with SCARA (selective compliance assembly robot arm) motions[J]. Chinese Journal of Mechanical Engineering, 2014,27(4): 693-702.

[7] Chebbi A H , Affi Z, Romdhane L. Prediction of the pose errors produced by joints clearance for a 3-UPU parallel robot[J]. Mechanism and Machine Theory, 2009,44:1768-1783.

[8] 陈炜，余跃庆，张绪平，等.欠驱动柔性机器人的动力学建模与耦合特性[J]. 机械工程学报,2006,42(6):17-23.

Chen Wei, Yu Yueqing, Zhang Xuping, et al. Dynamic modeling and coupling of underactuated flexible robot[J]. Chinese Journal of Mechanical Engineering, 2006,42(6):17-23.(in Chinese)

[9] 王庚祥，刘宏昭. 考虑球面副间隙的4-SPS/CU 并联机构动力学分析[J].机械工程学报,2015,51(1):43-50.

Wang Gengxiang Liu Hongzhao. Dynamics analysis of 4-SPS/CU parallel mechanism with spherical joint clearance[J]. Journal of Mechanical Engineering, 2015,51(1):43-50. (in Chinese)

[10]宋月娥,吴林,戴明. 机器人关节间隙误差分析[J]. 机械工程学报,2003,39(4):11-14.

Song Yuee, Wulin, Dai Ming. Error analysis of robot joint clearance[J]. Journal of Mechanical Engineering. 2003,39(4):11-14. (in Chinese)

[11]郭惠昕,岳文辉. 含间隙平面连杆机构运动精度的稳健优化设计[J]. 机械工程学报,2012,48(3):75-81.

Guo Huixin, Yue Wenhui. Design optimization of planar linkage mechanism with joint clearance for improving the robustness of kinematic accuracy[J]. Journal of Mechanical Engineering，2012,48(3):75-81. (in Chinese)

[12]汪劲松,白杰文,高猛,等. Stewart平台铰链间隙的精度分析[J]. 清华大学学报:自然科学版, 2002,42(6):758-761.

Wang Jinsong, Bai Jiewen, Gao Meng, et al. Accuracy analysis of joint-clearances in a Stewart platform[J]. Journal of Tsinghua Univresity: Science and Technology, 2002,42(6):758-761. (in Chinese)

[13]张宪民,刘晗.3-RRR并联机器人含间隙的运动学标定及误差补偿[J]. 华南理工大学学报:自然科学版,2014,42(7):97-102.

Zhang Xianmin, Liu Han. A clearance approach of kinematic calibration and error compensation for 3-RRR parallel robot[J]. Journal of South China University of Technology:Natural Science Edition,2014,42(7):97-102. (in Chinese)

[14]Chen Genliang, Wang Hao, Lin Zhongqin, A unified approach to the accuracy analysis of planar parallel manipulators both with input uncertainties and joint clearance[J]. Mechanism and Machine Theory , 2013,64:1-17.

[15]Frisoli A, Solazzi M, Pellegrinetti D,et al. A new screw theory method for the estimation of position accuracy inspatial parallel manipulators with revolute joint clearances[J]. Mechanism and Machine Theory, 2011,46:1929-1949.

[16]Jokin A , Isidro Z , Oscar A,et al. Improving static stiffness of the 6-RUS parallel manipulator using inverse singularities[J]. Robotics and Computer-Integrated Manufacturing, 2012,28:458-471.

[17]Amir R , Alireza A , Mohammad R,et al. An investigation on stiffness of a 3-PSP spatial parallel mechanism with flexible moving platform using invariant form[J]. Mechanism and Machine Theory , 2012,51:195-216.

[18]Sébastien B, Ilian A B. Accuracy analysis of 3T1R fully-parallel robots[J]. Mechanism and Machine Theory, 2010,45: 695-706.

[19]Sébastien B, Ilian A B. Pantopteron: a new 3T1R decoupled parallel manipulator for pick-and-place applications[J]. Mechanism and Machine Theory , 2010,45: 707-721.

[20]Paul R P. Robot manipulator: mathematics, programming, and control[M].Cambridge Massachusetts and London,England:The MIT Press, 1982:157-163.

[21]谷勇霞，杨天夫，郭峰.考虑多间隙的帆板式展开机构动力学分析[J]. 振动、测试与诊断，2015,35(1)：37-41.

Gu Yongxia, Yang Tianfu, Guo Feng. Dynamic performance of a solar array deployable mechanism with multiple clearances[J]. Journal of Virbration, Measurement & Diagnosis, 2015,35(1)：37-41. (in Chinese)

[22]陈隽，赵冠宇，陈鑫.线性时变动力系统参数识别方法与试验分析[J]. 振动、测试与诊断，2013,33(5)：832-838.

Chen Jun, Zhao Guanyu, Chen Xin. Parameter identification of linear time-varying dynamical system and experimental investigation[J]. Journal of Virbration, Measurement & Diagnosis[J], 2013,33(5)：832-838. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.03.024

教育部中央高校基本科研业务专项基金重点资助项目(JUSRP51316B)

2015-04-07；

2015-05-30

TH113； TH115

郑坤明，男，1989年8月生，硕士。主要研究方向为并联机器人优化和机械动态分析。 E-mail: ZhengKunming_111@163.com