非线性共振声谱法分析非对称边界条件下的一维缺陷

刘晓宙刘杰惠毛一葳何爱军

（1.近代声学教育部重点实验室，南京大学声学研究所 南京 210093）

（2. 南京大学 电子科学与工程学院 南京 210093）

非线性共振声谱法分析非对称边界条件下的一维缺陷

刘晓宙1刘杰惠1毛一葳1何爱军2

（1.近代声学教育部重点实验室，南京大学声学研究所 南京 210093）

（2. 南京大学 电子科学与工程学院 南京 210093）

线性共振声谱法可以用来检测含有线性弹性张量的物体缺陷，根据共振频率偏移、几何形状和密度共同确定在样本中的位置。但是如果是微小缺陷，应力和应变会呈现非线性关系，因此非线性共振声谱法是通过研究振幅和共振频率的关系来确定缺陷的位置和非线性的程度。本文采用非线性共振声谱法分析非对称边界条件下的缺陷，给出非对称边界经典非线性和非经典非线性下的共振频率偏移及高次谐波表达式，并且数值模拟结果表明此方法可以清楚分辨左、右缺陷的位置。

非对称边界 非线性共振声谱法 非经典非线性 经典非线性

超声检测法的优点是穿透能力较大，对平面型缺陷如裂纹、夹层等，探伤灵敏度较高，并可测定缺陷的深度和相对大小，设备轻便，操作安全，易于实现自动化检验。缺点是不易检查形状复杂的工件，要求被检查表面有一定的光洁度，并需有耦合剂充填满探头和被检查表面之间的空隙，以保证充分的声耦合。对于有些粗晶粒的铸件和焊缝，因易产生杂乱反射波而较难应用。此外，超声检测还要求有一定经验的检验人员来进行操作和判断检测结果。

超声无损评价有线性和非线性两种评价方法，其中线性方面的研究在国内外比较多，也取得了一定成果并应用于生产检测中。而非线性检测则是近些年才发展起来的，受到许多科学工作者关注的一种新方法。线性方法是相对较为传统的检测技术，主要有超声导波技术、声发射新技术、新型非接触超声换能方法及超声信息处理与模式识别等方法。导波技术对材料的SH模式导波、兰姆波、棒中导波等的简要分析来进行无损检测。管状结构是超声导波可发挥其特长的对象，用该技术可对各种管道进行长距离一次性检测。声发射技术是一种被动式检测技术，至今仍用于导弹壳体与潜艇的水压试验，以此对构件的安全性能与失效行为进行动态监测与评价。还有一种新型的非接触超声换能方法，主要有电磁声方法、静电耦合方法、空气耦合及激光超声方法，由于传统的方法需要使用耦合剂或采用水浸法来减少超声波在空气中的损失，因此许多物品不能用传统方法检测，这时就需要用非接触超声检测，它具有非接触，非侵入，完全无损的特点，使该技术有很好的应用前景。而在检测中的数字信号处理和数字识别能分离一些复杂的信号，减少许多误差。

长期以来，在研究声学的各种问题时，一直都是在线性声学的理论框架内进行和发展的。然而，在某些情况下，基于线性声学理论下的结果会带来较大误差，出现用线性声学无法解释的非线性现象。因此，在近年来，非线性声学得到科学家的广泛关注并获得快速发展。

非线性声学是一门既古老又年轻的学科，随着非线性声波信息价值的不断被发现，基于非线性声学的材料缺陷检测技术已获得越来越多的应用[1]。疲劳会使材料内部发生微结构的变化即出现不均匀性，并由于裂纹的萌生而存在大量界面，最近的理论和实验研究表明，所有这些都会对声二次谐波的非线性激发作出贡献，因此有理由认为，材料的非线性声学特性将随材料疲劳程度的不同而明显变化，非线性二次谐波激发技术是一种很有前途的无损疲劳检测方法[2]。

在二阶近似的条件下，固体的非线性是用若干个三阶弹性常数来描述的，对于各向同性的弹性体而言，有三个独立的三阶弹性常数。三阶或更高阶弹性常数是表征固体性质的宏观参数，它不但与固体结构有紧密的联系，而且将成为缺陷、疲劳等无损评价的新参数。裂纹的经典非线性效应是对裂纹的应力应变关系按照幂级数展开而得到的[3]。笔者分析弹性滞后效应及其本构方程，定性地讲，弹性之后类似于错位的Granato-Lucke滞后效应[4]。非线性效应不仅可以描述弹性滞后效应，还可以描述非弹性滞后效应。此类非线性效应与经典非线性效应有一个显著的区别在于，由滞后效应所引起的各个高次谐波的大小与基波的幅度成平方关系，而经典非线性效应中，第n次谐波与基波成n次方的关系。由此，可以很容易地判断裂纹所表现出的非线性关系为经典的还是非经典的。其他的裂纹非线性应力应变关系还包括双线性应力应变关系[5]，目前，对此类非线性应力应变关系有很广泛的研究，但是其缺点是其理论预言不会产生奇次谐波，而实验中却发现三次谐波的存在。对固体的非线性现象引起人们极大的兴趣，因为一来可以对这些固体的声非线性的机制进行研究，还有望利用这些非线性方法来进行无损检测。这些方法的可行性是基于声特性与结构的缺陷有很强的依赖性。这些材料对声的非线性响应是对缺陷程度的很好的反映，特别是岩石和混凝土材料表现出的非线性和滞后效应与一般或完好的材料相比有很大的不同[6]。共振声谱法是由Migliori[7]等发展起来的，此技术是基于测量共振峰的频率，它与自由悬挂的固体的密度、弹性模量、形状有关。非线性共振声谱法探讨和分析振幅与共振频率的依赖性，并利用这些信息来表征缺陷的位置和非线性的程度。这方面的例子有单模式的非线性共振谱法[8]，非线性波调制谱法[9]。刘晓宙等采用非线性方法对固体中的裂纹进行了系统地研究[10-15]，Van Den Abeele将非线性共振谱法推广到多模式的共振谱，主要是考虑模式之间的相互作用[16]，然而他所提出的方法无法解决对称问题，即无法判断缺陷是位于左端还是右端。本文笔者扩展此方法来解决这一问题，即采用一端自由，一端固定的边界条件，研究共振频率的偏移和经典、非经典非线性所引起的高频振幅。笔者发现这样拓展的非线性共振声谱法可以区分棒中左、右两端的缺陷。

1 理论

可以假设一均匀介质棒（棒的长度为L, 密度为ρ，声速为c）内存在缺陷(缺陷的长度为d,离声源的距离为xd)(见图1)。

图1 共振棒的几何示意

应力σ和应变ε的关系为:

式中：

ε=∂xu；

Δε —— 应变的幅度；

K —— 线性强度系数；

α —— 滞后非线性的强度；

β、δ —— 三阶和四阶弹性常数的组合代表经典非线性。

对两端自由的棒而言，对于经典非线性，共振频率的偏移与应变的平方成正比。然而笔者发现决定共振频率偏移的系数是关于棒中点对称的，所以此方法无法分辨缺陷是位于左边还是右边。对于非经典非线性而言，共振频率的偏移与应变成正比，而且也是关于棒中点对称。

在有外力作用下F，考虑衰减后的位移u(x,t)的波动方程[16]可以表示为：

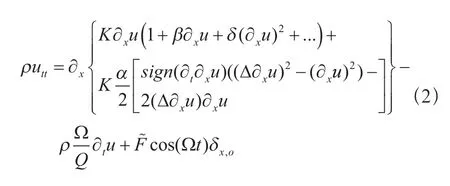
寻求方程(2)的解，将u分解为变量x和时间t的函数的乘积。

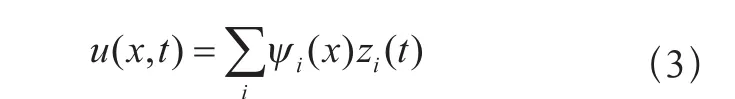
这里 {ψi（x)},i=-∞，...，+∞是一系列的空间函数，{zi(t)},i=-∞，...，+∞为一系列的时间函数。

一端自由和一端固定的边界条件为：

本征值为：

本征函数为：

将式（1）代入式（2）可得如下方程：

这里：

1.1 经典立方非线性的解

m模式振幅所满足的方程为：

这里：

因此，当响应振幅最大时的共振频率可以近似表示为：

因此：

图2(a)～图2(d) 来源于立方非线性缺陷的非线性参数C1,2m+1随缺陷位置的变化。

(a) C1,1—— 基波模式激发(m=0)；

(b) C1,3—— 第二模式激发(m=1);

(c) C1,5—— 第三模式激发(m=2);

(d) C1,7—— 第四模式激发(m=3)。

图2 比例系数C1,2m+1与缺陷位置的关系

由图2可见不同于两自由边界，C1,1在Xd=L处最大，而且C1,2m+1不再以中心为对称。

m模式附近的正弦激发的谐波的振幅：

三次谐波满足如下方程：

设：z3m=A3mcos(3Ωt+φ3m)经计算可得：

这里：

可得到系数C3,2m+1,C5,2m+1:

图3立方非线性引起的非线性参数C3,2m+1和 C5,2m+1随共振棒中的缺陷位置的变化。

(a) C3,1——基波激发（m=0)；

(b) C3,3——第二模式激发 (m=1)；

(c) C5,1——基波激发（m=0)；

(d) C5,3——第二模式激发 (m=1)。

图3 比例系数C3,2m+1和C5,2m+1与缺陷位置的关系

假定非线性为小量，共振频率可以表示为:

这里：

由图3可见C3,2m+1和C5,2m+1不再以棒的中点为对称。

1.2 非经典非线性的解

zm应满足如下方程：

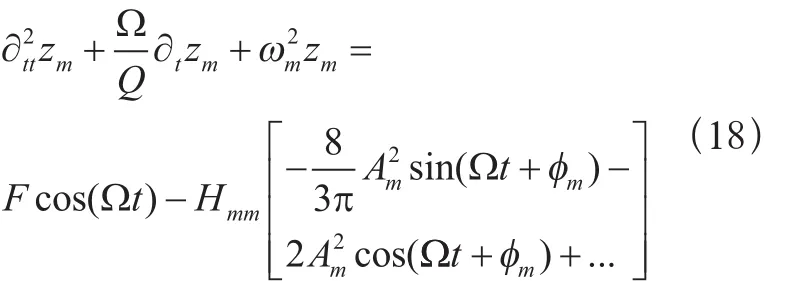
图4 比例系数X3,2m+1和X5,2m+1与缺陷位置的关系

图4来源于滞后非线性的参数X1,2m+1随共振棒中的缺陷的位置变化。

(a) X1,1——基波激发（m=0)；

(b) X1,3——第二模式激发 (m=1)。

从图4可以看到：X1,1与C1,1形状类似，但它们的值比C1,1要小得多。

同样在共振模式 ωm附近的三次和五次应变振幅可表示为：

图5(a)～图5(d)来源于滞后非线性的参数X3,2m+1和X5,2m+1随共振棒中的缺陷的位置变化。

(a) X3,1——基波激发（m=0)；

(b) X3,3——第二模式激发 (m=1);

(c) X5,1——基波激发(m=0)；

(d) X5,3——第二模式激发(m=1)。

由图5可见，X3,2m+1与C3,2m+1很相似，而X5,2m+1与C5,2m+1显著不同。

1.3 整体多模式非线性共振声谱法

对于以上的分析和计算，对任意特别模式的局部缺陷（不管是经典还是非经典），共振频率的偏移与在这一模式下的应变呈线性或平方关系。

因此可以写下如下的表达式：

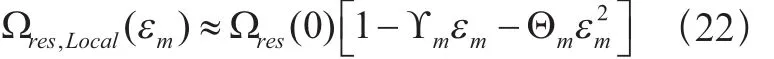
定义灵敏度函数：

这里：

为验证多模式的共振声谱法，假定棒中存在两个缺陷，一个为滞后非线性缺陷（αˆ=2000，d=L/50），位于50mm处，一个为经典的立方非线性缺陷（=-105，d=L/100），位于72mm处。图8说明灵敏度函数沿着棒中位置的空间分布，黑色代表预见的缺陷。图8可见明显的缺陷，位置与预计的一致，值得注意的是共振模式越多，缺陷的位置就越明显和精确。

为证明此方法可以区别左、右两端的缺陷，假定棒中有两个缺陷，一个在左端（αˆ=2000，d=L/50），一个在右端（=-105，d=L/100），位置分别为50mm和220mm, 结果见图9，图中明显可见左、右两个缺陷，因此此方法可以清楚区别左、右两边的缺陷，比两端自由边界条件的方法要好。

图6 灵敏度函数Ym随模数的变化

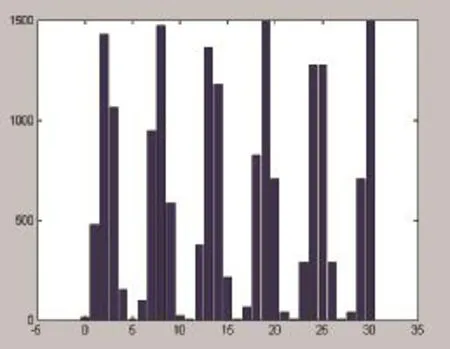
图7 灵敏度函数随模数的变化

图8 多模式的非线性共振声谱法重建含有左边两个局部缺陷的棒：一个滞后非线性和一个经典的立方非线性

图9 多模式的非线性共振声谱法重建含有左、右两个局部缺陷的棒：一个滞后非线性和一个经典的立方非线性(M=100)

2 结论

本文将多模式的非线性共振谱法拓展到非对称边界（一端自由和一端固定）。得到有经典和非经典非线性的缺陷棒中的共振频率偏移和高次谐波的表达式。笔者发现此方法可以识别两端自由边界条件下无法识别的左、右两边的缺陷，此方法还可以将灵敏度函数扩展到高维（二维和三维）。

[1] 刘晓宙，朱金林，尹昌，等．岩石等非线性介观弹性固体材料的谐波特性的超声研究[J]．物理学进展，2006，26(3)：386-389.

[2] Solodov I，Wackerl J，Pfleider K，et al．Nonlinear self-modulation and subharmonic acoustic spectroscopy for damage detection and location[J]．Applied physics letters, 2004，84(26)：5386-5388.

[3] Cleofé Campos-Pozuelo，Christian Vanhille，Juan A. Gallego-Juárez，Nonlinear Elastic Behavior and Ultrasonic Fatigue of Metals[J]．Universality of Nonclassical Nonlinearity，2006，3：443-465.

[4] Nazarov V E，Kolpakov A B，Radostin A V．Amplitude Dependent Internal Friction and Generation of Harmonics in Granite Resonator[J]．Acoustical Physics，2009，55(1)：100-107.

[5] Debaditya Dutta，Hoon Sohn，Kent A．Harries，et al．A Nonlinear Acoustic Technique for Crack Detection in Metallic Structures[J]．Structural Health Monitoring，2009，8(3)：251-262．

[6] Nazarov V E，Ostrovsky L A，Soustova I A，et al．Nonlinear acoustics of microhomogeneous media[J]. Phys. Earth Planet. Inter, 1988, 50: 65-73．

[7] Migliori A，Sarrao J L．Resonant Ultrasound Spectroscopy: Applications to Physics，Materials Measurements and Nondestructive Evaluation[M]．Wiley：New York，1997.

[8] Nazarov V E，Ostrovskii L A，Soustova，I A，et al．Anomalous acoustic nonlinearity in metals[J]．Akust．Zh，1988，34：491-499．[English transl.: Sov．Phys．Acoust．1988，34，284-289].

[9] Antonets V A，Donskoy D M，Sutin A M. Nonlinearvibrodiagnostics of flaws in multilayered structures[J]．Mech．Compos．Mater，1986，15：934-937.

[10] Yulin Feng，Xiaozhou Liu，Jiehui Liu，et al．The nonlinear propagation of acoustic waves in a viscoelastic medium containing cylinder micropores[J]. Chinese Physics B，2009，18(9)：3909-3917.

[11] Dao Zhou，Xiaozhou Liu，Xiufen Gong，et al．Damage diagnostics of concrete by using non-classical nonlinear acoustics means[J]. Chinese Physics B，2009，18(5)：1989-1995.

[12] 朱金林，刘晓宙，周到，等．声波在有裂纹的固体中的非经典非线性声传播[J]．声学学报，2009，34(3)：234-241.

[13] Li Quan，Xiaozhou Liu，Xiufeng Gong．Nonlinear nonclassical acoustic method for detecting the location of cracks[J]．Journal of Applied Physics，2012，112：054906.

[14] Jinlin Zhu, Ying Zhang, Xiaozhou Liu. Simulation of multi-cracks in solids using nonlinear elastic wave spectroscopy with a time-reversal process[J]．Wave Motion，2014, 51：146-156.

[15] Zhang Lue，Zhang Ying，Xiaozhou Liu，et al．Multi-cracks imaging using nonlinear nonclassical acoustic method[J]．Chinese Physics B，2014，23(10)：104301.

[16] Van Den Abeele K．Multi-mode nonlinear resonance ultrasound spectroscopy for defect imaging: An analytical approach for the one-dimensional case[J]. J．Acoust．Soc．Am．，2007，122(1)：73-90.

[国家重点研发计划（批准号：2016YFF20300)]

[国家自然科学基金项目（批准号11274166，11474160）]

[声场声信息国家重点实验室开放课题研究基金（批准号：SKLOA201609）]

Nonlinear Acoustic Resonance Spectroscopy Analysis of One Dimensional Defects under Non-symmetric Boundary

Liu Xiaozhou1Liu Jiehui1Mao Yiwei1He Aijun2
(1. Key Lab of Modern Acoustics, MOE, Institute of Acoustics, Nanjing University Nanjing 210093) (2. School of electronic science and engineering, Nanjing University Nanjing 210093)

Linear acoustic resonance spectroscopy method can be used to determine the position of the defects with linear elasticity tensors, which is dependent on the shift of the resonant frequency, geometric shapes and densities of the sample. But if there is a minor defect, there will be a nonlinear relationship between stress and strain, so the position and the extent of the defects can be determined through the relationship between the amplitude and the resonance frequency by nonlinear acoustic resonance spectroscopy. In this paper, using nonlinear resonance ultrasound spectroscopy to analysis the defects with non-symmetric boundary conditions, the expression of the shift of resonance frequency and the amplitude of the high harmonics are given under classical nonlinearity and non-classical nonlinearity, and the numerical simulation results show that this method can be used to clearly distinguish the left and right locations of the defects.

Non-symmetric boundary Nonlinear acoustic resonance spectroscopy Non-classical nonlinearity Classical nonlinearity

X924

B

1673-257X(2017)05-0019-07

10.3969/j.issn.1673-257X.2017.05.005

刘晓宙(1966～)，男，博士，教授，从事超声研究工作。

刘晓宙，E-mail: xzliu@nju.edu.cn。

2016-12-12）