基于FPGA的数控系统直线插补模块化设计*

沈孟锋，羊荣金，蒋水秀，何俊，胡冬生(杭州科技职业技术学院机电工程学院，杭州311402)

基于FPGA的数控系统直线插补模块化设计*

沈孟锋，羊荣金，蒋水秀，何俊，胡冬生
(杭州科技职业技术学院机电工程学院，杭州311402)

文章针对软插补器速度慢、计算复杂、精度不高等缺陷提出了采用可配置电子齿轮箱的硬件插补方案，建立了直线插补的算法模型。采用VHDL硬件描述语言设计了直线插补电子齿轮箱模块，搭建了运动控制多轴联动插补实验平台，伺服电机编码器反馈的实测数据为:在终点坐标为(5000，5000)的直线插补路径上，伺服电机实际运行最大偏差为1.4个脉冲当量，约为总行程的0.02%;在终点坐标为(3000，4000)的直线插补路径上，伺服电机实际运行最大偏差为4.2个脉冲当量，约为总行程的0.035%，实际偏差由伺服电机机械特性及传动刚性产生。由此表明:采用本插补方案的数控系统响应时间短、运行速度快、可靠性高，且不存在偏差累积误差，插补精确度高。

FPGA;数控系统;直线插补;模块化设计;伺服电机

0 引言

在数控系统中，插补算法的稳定性和精度对系统的性能指标具有重大影响。因此国内外科研人员一直在努力寻找一种精度高、速度快、稳定性好的插补算法，各知名数控系统企业如西门子、Fanuc等更是竭力保密插补运算这一核心技术，从不对用户开放［1-3］。

在数控系统众多插补算法的研究中，主要是针对复杂的曲线或曲面的轨迹加工，而普通的直线插补文献较少［1-2］。直线插补是最基本的插补，任何曲线都可由直线段逼近而成，因此提高直线插补的精度，对整个轨迹的形成具有重要的意义［3-4］。目前直线插补器多为软件插补器，虽然优点众多，但因其串行插补运算导致运行速度较低，不适用于高速、高精度的系统［4-5］。因此，众多学者采用EDA技术充分发挥硬件实时性的优势，设计研究了硬件直线插补器。文献［5］采用VHDL语言设计了包含X、Y向计数器和环形分配器的直线插补器提高了插补速度和可靠性，但该设计只进行微小距离仿真，未考虑电机实际运行的加减速情况。文献［6］基于FPGA实现数字积分法直线插补器简化了速度控制，但无法动态改变运动参数，运用范围有限。文献［7］给出了基于NiosII软核处理器的SOPC技术硬件直线插补控制器，其具有可编程、高数据处理速度、高扫描频率、高可靠性等优点，但其所占容量大，需外接SDRAM，同时也未考虑电机加减速控制情况。

本文提出了基于可配置电子齿轮箱的直线插补算法，其基本方法为:给出加工直线的运动轨迹，再计算出直线在各轴上的分量，然后计算各分量的最小公倍数，以此最小公倍数的量为虚拟轴，将虚拟轴产生的脉冲按各轴进行不同分频系数的分频，从而产生各个轴的分量脉冲(其中分频系数即传动比)。该方法的创新点在于:①各插补轴由硬件驱动并行运行，响应时间短，提高了系统运行速度和可靠性;②采取整数运算，且完成一次插补只需进行一次初始运算，不存在偏差积累误差，显著提高了系统精度;③可通过调节各轴分量来合成不同轨迹直线，灵活性高、易更新。

1 直线插补算法模型

基于可配置电子齿轮箱的直线插补法的各个跟随虚拟轴运动的实轴之间存在各自规划的协调运动关系。即X轴、Y轴乃至更多电机同时运动，它们的运动速度合成方向为二维直线AB方向或三维直线MN方向如图1所示。

图1 二维及三维直线加工

现作第一象限的二维直线AB:可设起点A坐标为(x1，y1)，终点B坐标为(x2，y2)。

则直线OA的水平分量脉冲数:

直线OA的垂直分量脉冲数:

采用DSP计算X轴、Y轴分量脉冲数的最小公倍数LCM:

以此最小公倍数LCM的值作为一虚拟轴的定长脉冲数，同时计算出各轴相对于虚拟轴脉冲的分频系数:

其中DX、DY分别为X轴、Y轴对虚拟轴脉冲的分频系数。X轴、Y轴跟随虚拟轴运行，直至虚拟轴结束，进而完成插补。在跟随的过程中，虚拟轴按照一定规律进行加减速运动，则各实轴也是成一定比例进行加减速运动，协调完成直线轨迹。

2 直线插补逻辑模块实现

实现二维直线插补需要完成的步骤有:①计算各轴分量、各分量的最小公倍数LCM、各轴对虚拟轴的分频系数，计算由DSP完成;②数据的输入输出，即FPGA与DSP的串口通信功能［8］;③产生虚拟轴脉冲功能，由加减速计算模块实现;④各轴驱动脉冲的产生，采用硬件描述语言(VHDL)实现变分频器的直线插补功能［9］。其逻辑结构框图如图2。

图2 直线插补模块逻辑结构框图

图中可知:先将所给直线的起始点坐标(x1，y1)和终点坐标(x2，y2)发送给DSP，DSP首先计算X轴、Y轴的分量脉冲数ΔX和ΔY，进而计算分量脉冲数的最小公倍数LCM，最后计算X轴、Y轴对虚拟轴脉冲的分频系数DX和DY;通过串口将计算结果发送给FPGA的串口通信模块。串口通信模块将最小公倍数LCM发送给加减速计算模块作为初始设定的定长脉冲数P;将分频系数DX和DY发送给直线插补器。加减速计算模块通过速度控制、计数比较产生虚拟轴驱动脉冲fa并将其发送给直线插补器。直线插补器内置多路分频器，能将虚拟轴驱动脉冲fa进行DX分频和DY分频，进而输出X轴驱动脉冲fx和Y轴驱动脉冲fy。驱动脉冲fx和fy与fa的总驱动时间一致，加减速驱动时间一致，它们的传动比为整数常量，脉冲频率变化相似，能够协调驱动各轴。各轴并行运行，无偏差运算，无累积误差，因此运行速度快、精确度高、灵活性好。

DSP求解最小公倍数LCM主要用到的方法是辗转相除法［10］，图3a为用C语言求两个数最小公倍数的程序框图，图3b为用C语言求三个数最小公倍数的程序框图。

图3 辗转相除法求最小公倍数的程序框图

本直线插补器内置的多路分频器采用奇偶等占空比的整数分频器［11］，一般整数的分频采用模N计数器便可轻松实现，可以理解为脉冲跟随系统时钟N次上升沿后才发出一个，随即清零或置位，再开始新一轮的循环的计数。采用上诉方法获得的输出脉冲脉宽与系统时钟是一致的，所以不会影响到上升沿触发的时序逻辑。本场合所生产的脉冲是用于驱动伺服电机，因此其占空比为50%就非常必要。该多路分频器就涉及到分频系数的奇偶性及占空比的相同性两种逻辑问题。

偶数分频较为简单，只要通过计数器即可完成此功能。本直线插补器需要的是占空比为50%的偶数N倍分频，具体实现过程为:首先设计一个计数器，对系统时钟进行上升沿触发计数，该系统时钟即为被分频的主时钟。接着等到计数器的值变为N/2－1时，翻转输出脉冲的高低电平，同时发送复位信号给上述计数器，让其进行下一个周期计数，此方法的高低电平反复翻转，便可得到任意占空比为50%的偶数分频。

为获得占空比为50%的N倍奇数分频，其实现过程较复杂一些，可以归纳为三步骤:第一步同样以模N (N为奇数)计数的方式对系统时钟上升沿触发，事先设定当计数器计到N时，对输出脉冲进行高低电平翻转，然后在计数到(N－1)/2也进行高低电平翻转，此时输出脉冲的占空比不是50%，但是经过了N分频。第二步与第一步同时进行，但是对系统时钟的下降沿触发，其它都与第一步相同，也可获得输出脉冲的占空比不是50%的N分频脉冲。第三步也是最关键的一步，就是将上诉两步产生的输出脉冲进行相或运算，便可得到占空比为50%的奇数N分频的输出脉冲。具体的原理见图4。

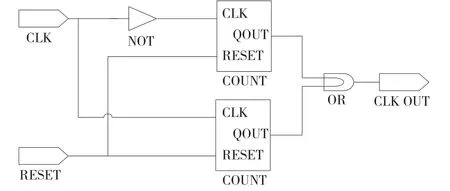
图4 奇数等占空比分频器原理图

3 直线插补实验验证

实验平台选用2台Panasonic公司Minas A4系列MCDDT3520伺服驱动器和2台适配MHMD082P1U伺服电机来实现二维直线插补这一功能，空间直线插补只需再增加一轴即可实现。本文采用硬件描述语言VHDL来描述直线插补器的逻辑关系，限于篇幅，本文不再给出相关源程序和详细原理图。对基于可配置电子齿轮箱的直线插补模块进行实验检测。

图5 实验平台实物图

实验过程中，系统时钟为50MHz，设置PLL倍频系数k为8。实验一:通过人机界面设置起始点坐标为(0，0)，终点坐标为(5000，5000)，由此X轴坐标分量与Y轴坐标分量相同，且它们的最小公倍数LCM也为5000，此时X、Y均为1分频。设置X轴编码器数据存于DSP的0X0090C0地址位，Y轴编码器数据存于0X00B800地址位。

图6 X、Y轴的位置曲线(实验一)

图6 为X、Y轴的位置曲线图，可知，X、Y轴的运行位置与设定的终点位置一致，所走过的脉冲数均为5000，所用时间均为591ms，且加减速运行过程也一致，均为7段S曲线加减速。图7为实验一设定下的X、Y轴的直线插补示意图，由此可知插补直线平滑，两轴同步完成插补。

图7 X、Y轴的直线插补(实验一)

图8 ΔD误差分析(实验一)

对该插补直线进行误差分析:计算由X、Y轴插补路径上的各个点与标准直线的垂直距离ΔD即为偏差值，首先通过起始点和终点坐标计算标准直线方程:

由此可计算路径上的任意点(Xt，Yt)与标准直线的距离ΔD:

误差百分比E即为偏差值ΔD与标准直线长度的比值:

图8即终点坐标为(5000，5000)时所作的误差分析图，代入公式可得所有加工路径上点的垂直距离ΔD的最大值为1.414214脉冲当量;算得误差百分比E为0.02%。

实验二:通过人机界面设置起始点坐标为(0，0)，终点坐标为(4000，3000)，由此X轴坐标分量与Y轴坐标分量不相同，此时DSP将计算出它们的最小公倍数LCM为12000，此时X轴为3分频，Y轴为4分频。同样设置X轴编码器数据存于DSP的0X0090C0地址位，Y轴编码器数据存于0X00B800地址位。

图9为实验二时的X、Y轴的位置曲线图，可知，X轴所走过的脉冲数为4000，所用时间为931ms。Y轴所走过的脉冲数为3000，所用的时间也为931ms。可见两轴的运行位置与设定的终点位置一致，且加减速运行过程也一致，均为7段S曲线加减速。图10为实验二设定下的X、Y轴的直线插补，两轴同时完成运行，插补直线平滑。

图9 X、Y轴的位置曲线(实验二)

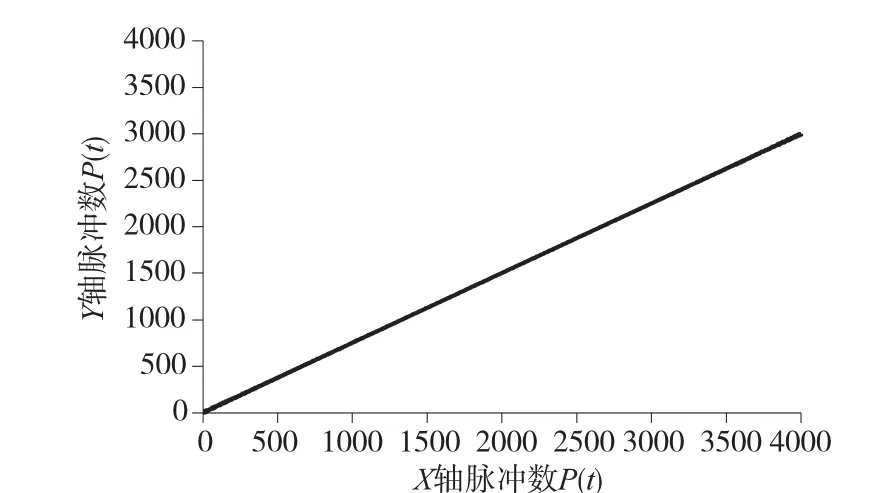
图10 X、Y轴的直线插补(实验二)

对该插补直线进行误差分析:其中图11即终点坐标为(4000，3000)时所作的误差分析图，代入公式(7)、公式(8)可得所有加工路径上点的垂直距离ΔD的最大值为4.2脉冲当量;算得误差百分比E为0.035%。

图11 ΔD误差分析(实验二)

4 总结

本文提出的基于可配置电子齿轮箱的直线插补算法思路清晰、设计简单，采用DSP将轨迹各轴分量算出，并求出各分量的最小公倍数设为虚拟轴，进而通过FPGA将虚拟轴产生的脉冲按各轴进行不同分频系数的分频，从而产生各个轴的分量脉冲。该方法逻辑关系、概念清晰易懂，执行速度快，占用资源少，运算简单，显著提高了各轴的运行速度和插补精度。基于本文，将进一步给出圆弧插补的模块化设计。

［1］左健民，朱兴华，汪木兰，等.基于FPGA的数控系统位置控制模块实现技术［J］.组合机床与自动化加工技术，2011(11):55－58.

［2］赵伟，黄莹，唐厚君.基于FPGA的多轴联动插补控制器的设计［J］.电气自动化，2013，35(2):68－77.

［3］岳云平.基于FPGA的高性能硬件NURBS曲线插补算法的研究和实现［D］.合肥:合肥工业大学，2015.

［4］熊睿，马国红，聂军.基于dsPIC的DDA插补算法设计与研究［J］.组合机床与自动化加工技术，2014(10):57－62.

［5］于海东.基于CPLD的直线插补控制器的设计与实现［J］.制造技术与机床，2009(1):66－69.

［6］陆悦，张峰，贺超.基于FPGA的直线插补器的研究与设计［J］.电气自动化，2010，32(1):27－43.

［7］崔桂梅，崔巍，庞海静，等.基于SOPC的硬件直线插补控制器设计［J］.微特电机，2011(5):56－61.

［8］李剑伟，周晨钟，皮佑国.基于FPGA的机床数控系统主从控制器通信研究［J］.组合机床与自动化加工技术，2014(12):109－112.

［9］吴红军，皮佑国.基于DSP和FPGA的运动控制器的设计与实现［J］.组合机床与自动化加工技术，2011(2): 75－82.

［10］王汝军.基于Matlab的辗转相除法［J］.电子设计工程，2015，21(9):21－23.

［11］周殿凤，康素成，王俊华.基于FPGA的任意数值分频器的设计［J］.信息化研究，2010，36(2):59－61.

(编辑李秀敏)

Modular Design of Linear Interpolation Control on CNC System Based on FPGA

SHEN Meng-feng，YANG Rong-jin，JIANG Shui-xiu，HE Jun，HU Dong-sheng
(School of Mechanical and Electrical Engineering，Hangzhou Polytechnic，Hangzhou 311402，China)

Regarding the softw are interpolation has the disadvantages of slow speed，complex calculation and low precision，studied for linear interpolation operation.Thereby，interpolation schemes employing reconfigurable electronic gear boxes are developed and the corresponding application algorithms are carried out.Similarly，by using the VHDL language，interpolation modules for linear interpolation is designed and realized.Hence experiment platform for multi-axis linage control is set up.The experimental data shows that within a terminal point coordinate(5000，5000)，the maximum deviation of linear interpolation is below 2 pulses for the executed result of physical mechanism，w hich is approximately 0.02%of the full track.And within a terminal point coordinate(3000，4000)，the maximum deviation is below 5 pulses，which is about0.035% of the radius.The actualdeviation is caused by the mechanicalcharacteristics and the transmission rigidity of the servo motor.Therefore，The numerical control system with the interpolation scheme has the advantages of short response time，fast running speed，high reliability，no error accumulation error and high interpolation precision.

FPGA;CNC system;linear interpolation;modular design;servo motor

TH166;TG659

A

1001－2265(2017)04－0118－04

10.13462/j.cnki.mmtamt.2017.04.030

2016－12－02;

2017－01－04

杭州科技职业技术学院2016年度科研课题(HKZYYB－2016－13)

沈孟锋(1990—)，男，杭州人，杭州科技职业技术学院助教，硕士，研究方向为数字运动控制技术，(E－mail)shenmengfeng@163.com;

羊荣金(1978—)，男，杭州人，杭州科技职业技术学院高级工程师，硕士，研究方向为电气与自动化技术。