均匀网络上SIS传染病模型几种对逼近方法的比较

李 星，罗晓峰

(山西大学 a.复杂系统研究所； b.数学科学学院；c.计算机与信息技术学院，太原 030006)



均匀网络上SIS传染病模型几种对逼近方法的比较

李 星a,b，罗晓峰a,c

(山西大学 a.复杂系统研究所； b.数学科学学院；c.计算机与信息技术学院，太原 030006)

网络传染病模型的精度是评价模型优劣的标准，其中网络对逼近传染病模型的优劣取决于所选逼近方法的精度。借助SIS传染病模型比较均匀网络上染病邻居数服从泊松分布、多项分布以及基于平均场思想的3种逼近方法的精度，发现在泊松分布下模型的误差最小，即泊松分布下的逼近方法精度最高。

均匀网络；对逼近；传染病；基本再生数；随机模拟

传染性疾病一直影响着人类的生活，有的甚至威胁着人们的生命，如非典(SARS)、艾滋病(HIV)、埃博拉等，因此对传染病传播的研究显得尤为重要[1]。由于在人群中进行疾病实验具有不可行性，因此数学模型可作为强大的工具来模拟实际疾病在人群中的传播机理，进而预测疾病的发展趋势，做出预防和控制策略。所以，传染病数学模型的精度成了能否精准预测疾病发展趋势的关键[2-4]。另外，由于疾病在人群中传播，人与人之间的接触关系(人群结构)对疾病的传播也起着至关重要的作用。随着网络科学的发展，研究者把人群映射到网络上，通过网络拓扑结构体现人群内部的结构，进而建立基于网络的传染病模型来研究疾病在人群中的传播[5-8]。在网络中，节点代表人群中的个体，节点之间的连边代表人与人之间的接触关系。网络对逼近模型是网络传染病模型的一种，它以节点和边作为变量建立传染病动力学模型，进而研究疾病的传播机理[9-10]。这类模型的精度取决于所选逼近方法的精度，因此本文主要借助均匀网络(个体之间接触关系的差异性不大)上的SIS传染病模型比较了3种逼近方法(即染病个体数服从泊松分布、多项分布以及基于平均场理论)的精度。

1 均匀网络模型

对于SIS对逼近传染病模型,设个体总数为N且保持不变，即网络节点总数不变，个体按状态分为易感者S和染病者I，染病者恢复后变为易感者，一个染病者和一个易感者每次接触传染的概率为τ，染病者的恢复率为γ。对于[S]、[I]、[SI]、[SS]、[II]，利用主方程可得

式中：[A]表示状态为A的总节点数；[AB]表示状态为A和状态为B的节点构成的所有二元组(对)数量；[ABC]表示状态为A、状态为B和状态为C的节点构成的所有三元组数量。假设网络的平均度为n1，显然有如下保持量：

(1)

接下来通过不同的逼近方法封闭模型进行研究。

1.1 泊松分布下的SIS对逼近模型(P-PW)

(2)

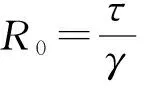
1.2 多项分布下的SIS对逼近模型(B-PW)

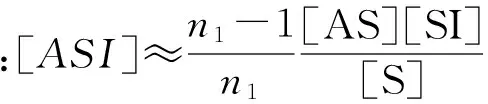
(3)

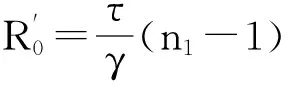
1.3 平均场SIS对逼近模型(MF-PW)

Kiss等在文献[11]中应用平均场的想法给出三元组的逼近公式：

可得到相应的平均场SIS对逼近传染病模型(MF-PW)：

(4)

接下来利用无病平衡点的稳定性计算该模型的基本再生数。

令系统(4)的右边3式为0，得到系统的无病平衡点Q0(N,0,n1N)。该系统在无病平衡点Q0处的Jacobian矩阵为

(5)

因此， Jacobian矩阵(5)的特征方程为|λE-J0|=0， 即

(6)

显然，特征方程(6)有一个负实根-γ，当且仅当

的所有特征根有负实部时，无病平衡点Q0是局部渐近稳定的。由于h(λ)的判别式为

因此，不妨设h(λ)的特征根分别为λ1、λ2。由圆盘定理可知，两特征根必须有负实部满足以下条件：

(7)

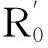
下面将针对各模型及其基本再生数进行随机和数值模拟对比，并进行误差分析，进而比较3种逼近方法的精度。

2 模拟与误差分析

这部分在ER随机网络(均匀网络)[12]上通过3种模型(式(2)(3)和(4))进行数值与随机模拟(100次求平均)比较3个模型的准确性。误差分析结果表明模型(2)误差最小，即染病邻居服从泊松分布的逼近方法更合理。

首先，构造一个总节点数为N=5 000的度分布服从泊松分布pk=P(λ)的配置网络，其中,λ=20。该网络的总边数为n1N=1.000 0×105，平均度n1=20.0。

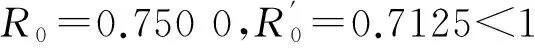
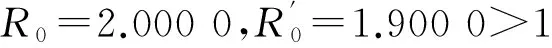
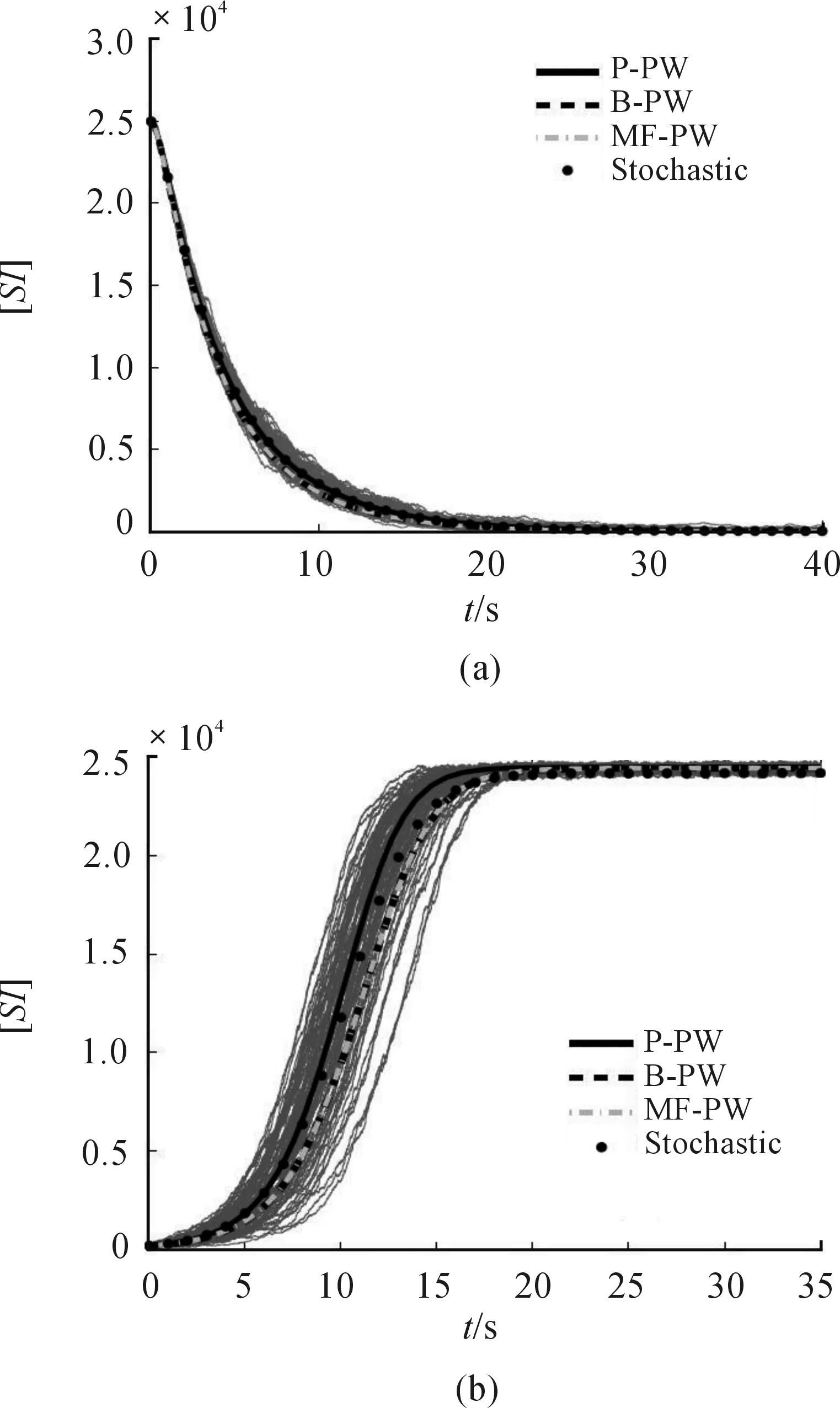
图1 在平均度为20、总节点数为5 000的ER随机网络下[SI]的时间序列

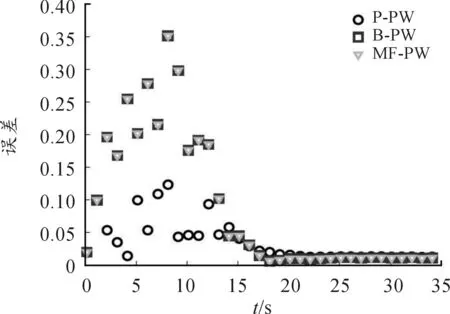
图2 ER随机网络时误差随时间的变化情况

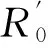
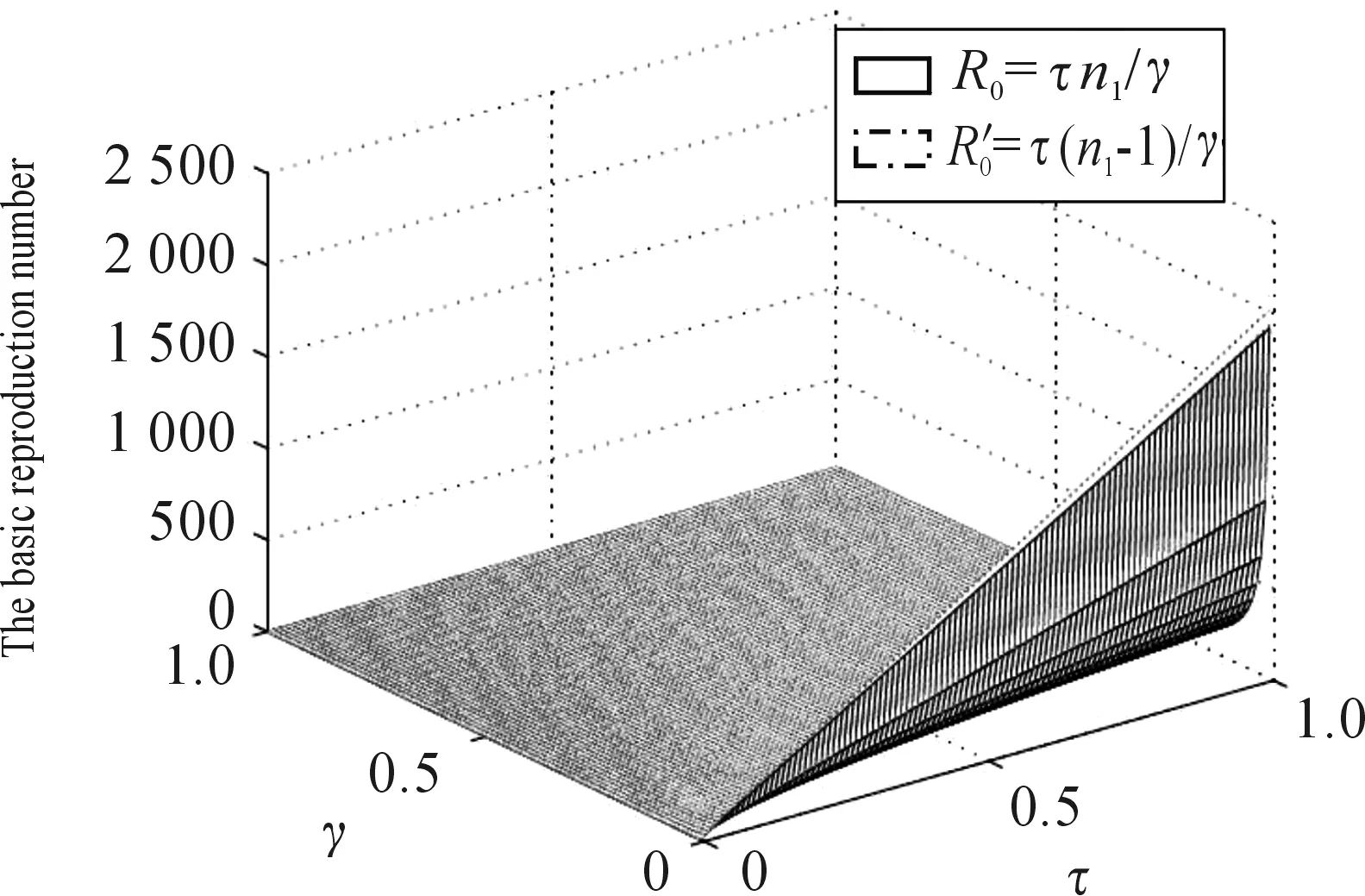
图3 ER随机网络R0和随τ，γ的变化情况

3 结束语

疾病在人群中的传播不仅与疾病本身的传播机理有关，且取决于人群个体的分布。网络传染病模型就是基于此，把人群的分布映射到网络上，然后让疾病在网络上传播。模型的高准确性是建模者所追求的，既有利于数学分析又能应用到实际疾病研究中。本文研究了均匀网络考虑染病邻居数服从泊松分布、多项分布以及基于平均场思想3种不同逼近方法的SIS模型，对模型求解，发现染病邻居数服从泊松分布的逼近方法得到的疾病阈值略大于其他两种。通过模拟与误差分析，得到染病邻居数服从泊松分布的逼近方法误差最小。

[1] 靳祯，孙桂全，刘茂省.网络传染病动力学建模与分析[M].北京：科学出版社，2014.

[2] ANDERSON R M,MAY R M,ANDERSON B.Infectious diseases of humans:dynamics and control[M].Oxford:Oxford university press,1992.

[3] HETHCOTE H W.The mathematics of infectious diseases[J].SIAM review,2000,42(4):599-653.

[4] KEELING M J,ROHANI P.Modeling infectious diseases in humans and animals[M].Princeton ：Princeton University Press,2008.

[5] KEELING M J,EAMES K T D.Networks and epidemic models[J].Journal of the Royal Society Interface,2005,2(4):295-307.

[6] MOTTER A E,MATíAS M A,KURTHS J,et al.Dynamics on complex networks and applications[J].Physica D:Nonlinear Phenomena,2006,224(1):vii-viii.

[7] FU X,SMALL M,WALKER D M,et al.Epidemic dynamics on scale-free networks with piecewise linear infectivity and immunization[J].Physical Review E,2008,77(3):036113.

[8] PASTOR-SATORRAS R,CASTELLANO C,VAN MIEGHEM P,et al.Epidemic processes in complex networks[J].Reviews of modern physics,2015,87(3):925.

[9] LUO X F,ZHANG X,SUN G Q,et al.Epidemical dynamics of SIS pair approximation models on regular and random networks[J].Physica A:Statistical Mechanics and its Applications,2014,410:144-153.

[10]MORRIS A J.Representing spatial interactions in simple ecological models[D].Warwick ：University of Warwick,1997.

[12]ERDDS P,WI A R.On random graphs I[J].Publ Math Debrecen,1959(6):290-297.

(责任编辑 陈 艳)

Comparison of Several Pair-Approximation Methods for SIS Epidemic Models in the Homogeneous Networks

LI Xinga,b, LUO Xiao-fenga,c

(a.Complex System Research Center; b.School of Mathematical Sciences; c.School of Computer & Information Technology, Shanxi University, Taiyuan 030006, China)

The accuracy of network-based epidemic models is a criterion of judging these models. Interestingly, judging the pair-approximation models in networks depends on the accuracy of approximation methods. Via SIS models, we compared the accuracy of three approximation methods in the homogeneous networks. The first is based on the number of infected neighborhoods of individuals following Poisson. The second is based the number of infected neighborhoods of individuals following multinomial distribution. The last one is based on the mean-field theory. Then we find the model under Poisson distribution with smallest errors, i.e. the accuracy of approximation methods under Poisson distribution is highest.

homogeneous network; pair-approximation; epidemic; basic reproduction number; stochastic simulation

2016-12-08 基金项目：国家自然科学基金青年科学基金资助项目(11501340)；山西省回国留学人员重点科研资助项目(2013-重点3)

李星(1990— )，女，硕士研究生，主要从事复杂网络及其传播，E-mail:lixing20469@gmail.com；罗晓峰(1987—)，男，博士研究生，主要从事网络传播动力学研究，E-mail:luo_xf1988@163.com。

李星,罗晓峰.均匀网络上SIS传染病模型几种对逼近方法的比较[J].重庆理工大学学报(自然科学)，2017(5):169-173.

format：LI Xing, LUO Xiao-feng.Comparison of Several Pair-Approximation Methods for SIS Epidemic Models in the Homogeneous Networks[J].Journal of Chongqing University of Technology(Natural Science)，2017(5):169-173.

10.3969/j.issn.1674-8425(z).2017.05.028

O175

A

1674-8425(2017)05-0169-05