基于SV-POT模型的黄金市场的动态VaR预测
苏理云,王 杰
(重庆理工大学 理学院,重庆 400054)
基于SV-POT模型的黄金市场的动态VaR预测
苏理云,王 杰
(重庆理工大学 理学院,重庆 400054)
针对黄金市场呈现的“尖峰厚尾”和波动持续性等特征,选用SV(stochastic volatility)模型来刻画。将SV模型与基于POT(peak over threshold)模型的极值理论相结合,建立SV-POT的组合模型,预测该金融市场的动态VaR(value at risk)。最后,与GARCH-POT模型相比得出:基于随机波动模型的SV-POT模型在一定程度上能更精确地预测动态VaR。
SV模型;极值理论;POT模型;VaR
2002年10月上海黄金交易所的成立使我国黄金市场逐步市场化,给更多的个人和机构投资者提供了一个良好的平台。正常情况下,黄金是规避风险增加利益的较好选择。而现实中,黄金也像其他金融投资品一样面临着亏损等风险。
黄金价格受多方面的因素影响,包括原油价格、利率水平等。除此之外,黄金价格还受到中央银行增减黄金储备、金融危机以及南非局势等突发事件的影响[1]。因此,黄金市场的风险预测尤为重要。Jorion详细介绍了VaR的概念和各种计算模型,将VaR定义为“在一定置信水平下,金融资产或投资组合在特定时间段内可能遭受的最大损失”,很好地将预期损失量与发生的可能性结合起来。但传统的计量模型都将金融序列假设为正态分布,与实际金融市场的波动情况不符。因此,金融序列波动率的预测在风险测量中始终占据至关重要的地位。经典的GARCH类模型有较多的扩展类研究,被证明可以拟合金融市场的收益率[2-3];而Taylor[4]提出的随机波动(stochastic volatility,SV)模型将隐含波动率引入自回归方程中,更灵活有效地刻画了金融市场的波动性,且被证明更有助于刻画金融市场的本质特征[5-8]。但由于SV模型精确似然函数较难得到,所以参数估计一直是个难题。近年来,随着计算机技术的发展,Jacquier等[9]首次应用马尔科夫链蒙特卡洛(markov chain monte carlo, MCMC)方法估计SV模型的参数。国内SV的学者如朱慧明[10]、苏理云[11]进一步研究了基于Gibbs抽样的MCMC方法,可以得到最佳的模型的参数估计结果。Francois[12]针对金融市场中的极端情况研究了极值理论,提出了压力测试下的风险度量方法。随着研究发现,我国的金融市场收益大多不服从独立同方差假设,且往往是非正态分布。所以,考虑用条件异方差模型刻画收益的动态变化,在此基础上计算动态VaR值。国内研究最多的是用GARCH族模型和SV模型对VaR的度量[13],却很少将波动率模型与极值理论的组合模型相比较,关于SV模型与极值理论的组合模型的研究也较少。所以,本文将SV模型与极值理论相结合,建立SV-POT模型预测黄金市场的尾部风险,并与GARCH-POT模型做对比,为黄金市场的风险管理寻找较优的预测模型。
1 波动率模型的提出
1.1 SV-N模型
SV模型不仅含有随机波动的因素,而且还考虑了方差的噪声过程,并认为方差和噪声都是不可观测的随机变量。SV-N模型的具体表达式如式(1)所示:
(1)
其中:at表示去均值后的第t期的对数收益率;ht表示at潜在的对数波动率;α和φ为常数,其中φ为持续性参数且|φ|<1,反映了当前波动对未来波动的影响;ηt代表了波动过程中其他外在扰动,独立同分布于正态分布。εt和ηt互不相关,模型中待估参数有α,φ和ση。
1.2SV-T模型
当εt服从正态分布时,随机变量仍会出现比正态分布较厚的尾部。针对这一现象,很多学者开始考虑拓展变量误差项εt的分布,Liesenfeld和Jung提出了SV-t模型,能较准确地刻画实际收益序列的波动性。
SV-t模型的具体形式如下所示:
(2)
式(2)中,εt服从标准化学生t分布,自由度为v,其分布的概率密度函数为
(3)
当自由度v<4时,其峰度不存在;当自由度v>4时,其峰度大于3;当自由度v趋于无穷大时,该分布退化为标准正态分布。待估参数有α,φ,ση和v。
对于SV模型的参数估计,本文选择运用MCMC 方法。该方法的本质是加入待估参数的先验信息,利用Gibbs抽样方法得到收敛平稳的马尔可夫链,密度函数记为π(x),该分布即可看成参数的后验分布。该方法的缺点是计算较为复杂,优点是问题维数的增加不会降低其收敛速度或者使其更复杂。
1.3 GARCH模型
经典的GARCH(p,q)模型具体表达式如下所示:
(4)
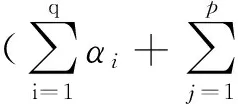
对于相对复杂的SV模型得到的分布函数来讲,通过样本分布函数的有限阶矩可知晓其中数据含有的特征和基本信息。而在统计的研究分析中,认为样本量的期望均值为一阶矩,变量的方差为二阶矩。由波动方程ht=α+φ(ht-1-α)+ηt可知:
(5)
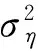
(6)

2 基于SV-POT的动态VaR模型

(7)
分布中有2个未知参数,分别是形状参数ξ和位置参数β,其中β>0,且当ξ>0时,x≥0;当ξ<0时,0≤x≤β/ξ。又因为F(u)=(N-Nu)/N,Nu表示样本中超过阈值u的个数,N为样本总数。估计形状参数和位置参数的前提是确定阈值的大小。由于阈值的确定不是本文的重点,所以本文选用超额均值函数图法。确定阈值后,用极大似然估计法可得形状参数ξ和位置参数β的估计。根据VaR理论,在置信水平为p时,可推导出对数收益率的风险值为:
(8)
最后将SV模型与VaR方法结合,得到的SV-POT-VaR模型为:
3 黄金市场的实证研究
本文以上海黄金交易所AU99.99每日收盘价数据为样本,选取2002年11月1日至2016年10月18日的共3 399个数据进行分析。数据来源于RESSET数据库。令yt=100(lnpt-lnpt-1),得到对数收益序列,其中pt为t时刻的价格指数。
由图1可以看出:黄金价格基本呈现直线上升趋势。因为随着金融市场的开放和不稳定性,越来越多的人认识到黄金具有增值保值的功能,为了规避资产贬值等风险而选择购买黄金,使黄金的价格持续走高。从2012年以后,由于美国经济的恢复等因素,规避风险的资金流出较多,给黄金市场形成一定的压力,价格涨跌起伏。

图1 黄金价格波动
由于黄金价格的对数收益率可以很好地反映其波动情况,从图2可看出黄金价格对数收益率呈现的异方差现象。在2013年4月,黄金价格突然暴跌,在金融界引起一场大的风波。类似于这种极端情况近年来比比皆是,因此黄金市场的风险度量备受关注。

图2 对数收益序列{at}的时序
图3是黄金对数收益序列的正态性检验,直线代表正态分布的分位数,散点代表黄金对数收益序列的分位数。散点相对于直线的偏离程度较大,所以黄金对数收益序列并不服从正态分布。

图3 对数收益序列的Q-Q图
表1是黄金对数收益序列的基本统计描述,其中偏度值为负,峰度值远远大于3,说明该序列具有“尖峰厚尾”特性,J-B统计量对应的P值为0,ADF检验在在5%水平下显著,应拒绝原假设,即该序列为平稳的非正态分布。综上描述,建立异方差模型,
运用极大参数估计方法,得到模型的参数估计,结果如表2所示。

表1 黄金对数收益率的统计特征
注:其中*表示在5%水平下显著。

表2 基于不同分布的GARCH(1,1)模型的参数估计
由表3可知:F检验统计量和LM统计量的P值均大于0.05,因此可认为建立GARCH模型后的异方差已消除。GARCH模型能较好地刻画该序列的波动性。得出GARCH模型的波动方程为:
GARCH-N模型:
GARCH-T模型:
由表2可以看出:基于学生t分布的AIC值比基于正态分布的AIC值小。因此,基于学生t分布的GARCH模型能较好地拟合该序列。
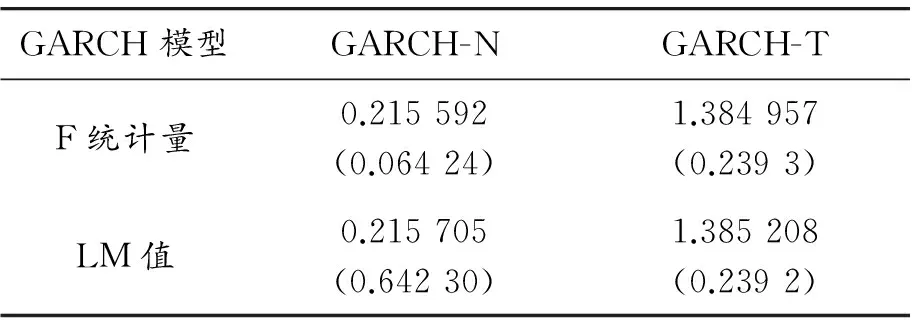
表3 标准化残差后的ARCH-LM检验
SV模型的参数估计借助Winbugs软件实现,Gibbs抽样为30 000次,并舍弃前15 000个“燃烧期”。 因为在Markov链收敛前,各状态的边际分布还不能认为是平稳的,所以用后15 000个抽样值为各参数估计的稳定分布抽样。参数估计结果如表4所示。
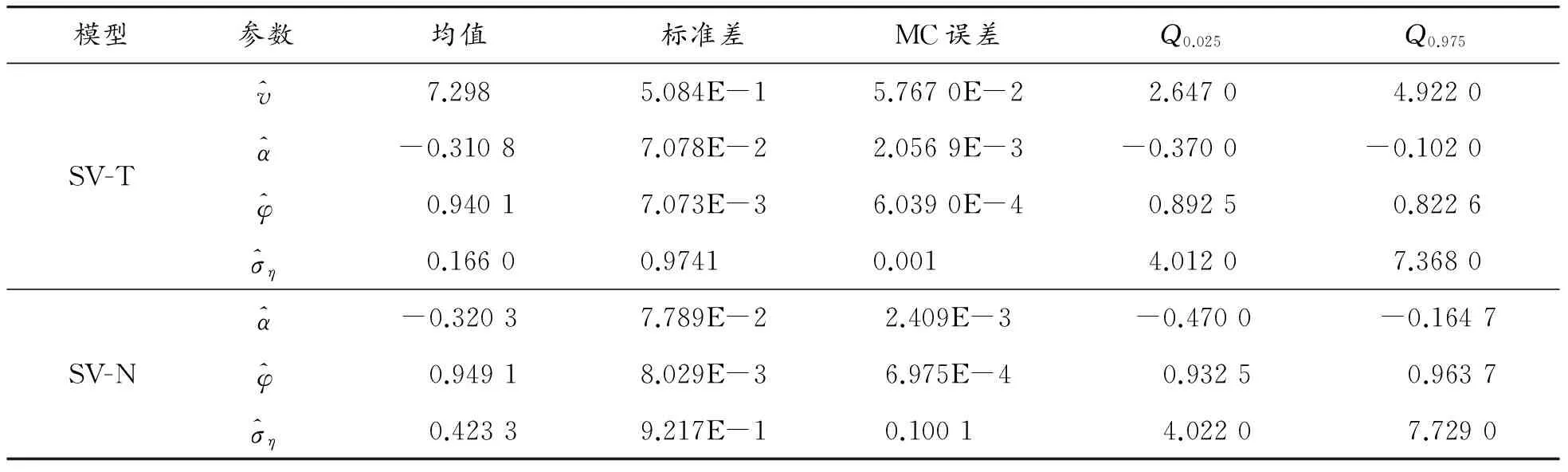
表4 SV模型参数估计结果及统计检验
注:表中MC误差为蒙特卡罗(Monte Carlo)误差,与标准差相比越小,则参数估计越精确,其中mEn表示m×10n。
得到SV-N模型的波动方程:
ηt~i.i.dN(0,0.423 32)
SV-T模型的波动方程:
ηt~i.i.dN(0,0.166 02)
其中自由度为7.298。
得到黄金对数收益的波动模型后,将数据标准化可以得到独立同分布的标准残差序列,结合极值理论的POT模型预测VaR。通过超额函数法和极大似然估计法,分别得到阈值u和形状参数和位置参数的估计值,结果如表5所示。

表5 基于SV-T模型的POT模型参数估计
基于各类波动模型的POT模型中,由于参数估计方法完全一样,所以这里仅用SV-T模型为例分析。
图4给出了标准残差序列拟合GPD的诊断检验图,分别为超出量分布图(左上)、残差散点图(左下)、尾部分布图(右上)以及残差QQ图(右下)。其左上图表示超出量分布的GPD分布拟合状况,左下图表示对尾部分布的估计,两图中的实线均为参照线;对于右上图而言,拟合曲线穿过散点密集区,而在右下图中散点紧密围绕直线分布,均反映出良好的拟合状态。在得到波动方程和POT模型分布后,就可以得到动态VaR的预测模型。但预测结果难免会出现一些误差,因此需要进行正确率检验。本文用2002年11月1日至2014年12月31日(共2 964个观测值),作样本来估计模型的参数;用剩下的435个观测值,用来对模型的评估检验。这里用Kupiec[18]提出的失败率检验法。似然比统计量(LR)表示为:
(10)
其中:N表示失败次数;T代表观察总数;p=N/T表示失败率,期望失败率为p′。即将模型好坏的评估转化为失败率p是否显著不同于期望失败率p′。在原假设条件下,LR服从自由度为1的卡方分布。
从表6检验结果可以看出:GARCH-POT模型预测VaR的失败次数较低,虽然远远低于可接受的失败次数,但比较保守的风险预防会令投资者失去很多投资机会,因此并不合适。SV-T-POT模型与SV-N-POT模型相比,失败次数均在接受区间内,因此效果更优。
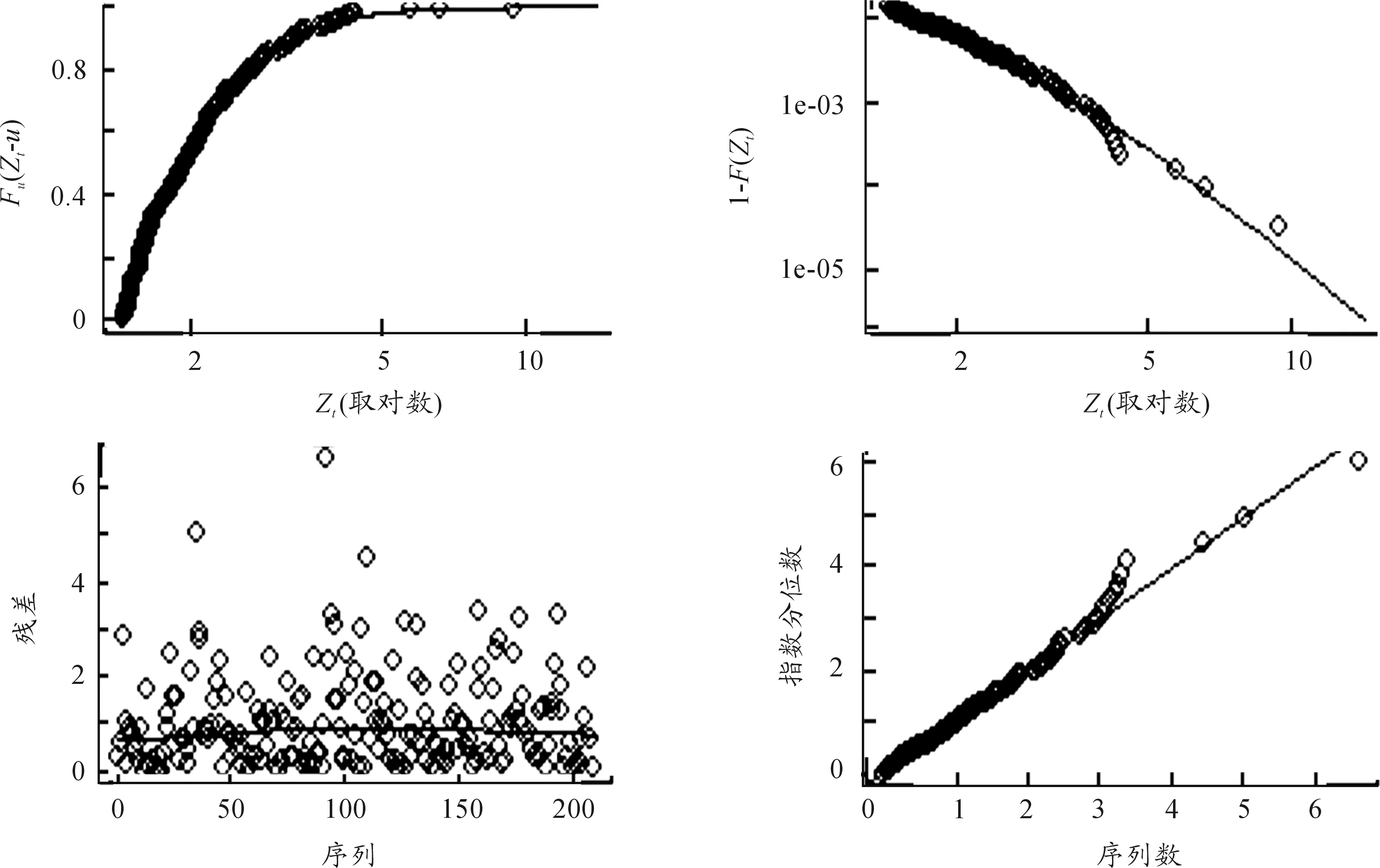
图4 标准残差序列GPD的诊断检验图

置信水平接受区间失败次数GARCH-N-POTGARCH-T-POTSV-N-POTSV-T-POT95%14≤N≤3057152097.5%5≤N≤84610899%2≤N≤41354
图4给出了95%置信水平下,两种不同模型得到的动态VaR与实际对数收益序列的对比。将两类能够较好刻画序列厚尾性的模型进行对比,GARCH-T-POT模型得到的动态VaR明显低于SV-T-POT模型,表明SV-T-POT模型计算得到的VaR值能更准确地预测黄金市场的风险。

图4 95%置信水平下不同模型的VaR对比
图5展示了4种不同模型在95%置信水平下的动态VaR与对数收益序列的线性对比图。可更清晰地看出:相对于SV类模型,GARCH模型预测的VaR过于保守,而SV-N-POT模型的拟合比SV-T-POT模型低估了VaR。

图5 95%置信水平下不同分布的VaR对比
4 结论
本文旨在寻找能较精确预测VaR的模型,将不同分布的假设的波动率模型与极值理论相结合,并进行对比分析。结果得出:基于厚尾t分布的SV模型不仅能更好地拟合序列的波动特性,与极值理论相结合构成的SV-T-POT模型,在预测VaR方面优于其他模型。进一步拓展了金融风险度量领域的应用,为投资者提供了可靠的投资依据,避免更多的风险损失。
[1] 王开科.我国黄金现货市场极端风险度量-基于POT方法的分析[J].南方金融,2015(9):59-67.
[2] 房小定.基于GARCH族模型族的创业板指数波动性研究[J].金融经济(理论版),2014(4):104-106.
[3] NARAYAN P K,LIU R,WESTERLUND J.A GARCH model for testing market efficiency[J].Journal of International Financial Markets Institutions & Money,2016,41:121-138.
[4] TAYLOR S J.Modeling financial time series[M].Chichester:John Wiley and Sons,1986.
[5] AIT-SAHALIA Y,AMENGUAL D,MANRESA E.Market-based estimation of stochastic volatility models[J].Journal of Econometrics,2015,187(2):418-435.
[6] KASTNER G.Dealing with Stochastic Volatility in Time Series Using the R Package stochvol[J].Journal of Statistical Software,2016,069(5):1-30.
[7] CHAN J,GRANT A L.Modeling Energy Price Dynamics:GARCH versus Stochastic Volatility[J].Energy Economics,2015,54:182-189.
[8] 余素红,张世英.SV和GARCH模型拟合优度比较的似然比检验[J].系统工程学报,2005,19(6):625-629.
[9] JACQUIER E,POISON N G,ROSSI P E.Bayesian Analysis of Stochastic Volatility Models[J].Journal of Business & Economic statistics,1994(12):371-389.[10]朱慧明,李峰.基于MCMC模拟的贝叶斯厚尾金融随机波动模型分析[J].运筹与管理,2007,16(4):111-115.
[11]苏理云,彭相武,王杰.基于状态空间SV-T-MN模型的股指波动率预测[J].数理统计与管理,2016(5).
[12]LONGIN F M.From value at risk to stress testing:The extreme value approach[J].Journal of Banking & Finance,2000,24(7):1097-1130.
[13]周炳均,王沁,郑兴.基于两种分布下的SV模型与GARCH模型的VaR比较[J].重庆文理学院学报(社会科学版),2016(5):133-137.
[14]胡晓馨.基于极值理论的黄金期货市场风险度量研究[D].杭州:浙江大学,2014.
[15]MCNEIL A J. Calculating quantile risk measure for financial time series using extreme value theory[J].ASTIN Bulletin,2000,27(1):117-137.
[16]桂文林,韩兆洲.POT模型中GPD“厚尾”性及金融风险测度[J].数量经济技术经济研究,2010(1):107-118.
[17]耿贵珍,王慧彦.基于POT-GPD模型的地震巨灾损失分布研究[J].自然灾害学报,2016(3):153-158.
[18]PAUL H K.Techniques for Verifying the Accuracy of Risk Measurement Models[J].The Journal of Derivatives,1995,3(2):73-84.
(责任编辑 何杰玲)
VaR Forecasting for Gold Market Based on SV-POT Model
SU Li-yun, WANG Jie
(College of Science, Chongqing University of Science and Technology, Chongqing 400054, China)
The SV (Stochastic Volatility) model is used to depict the characteristics of the “fat tail” and volatility persistence in the gold market. Then combining the SV model with the extreme value theory based on POT (Peak Over) model, the combination model of SV-POT is established to predict the dynamic VaR of the financial market. Finally, compared with the GARCH-POT model, the SV-POT model based on stochastic volatility model can predict VaR (Value at Risk) more accurately in a certain extent.
SV model; extreme value theory; POT model; VaR
2016-12-25 基金项目:国家自然科学基金资助项目(11471060);重庆市教育委员会人文社会科学研究一般项目(15SKG136);重庆市教育科学规划课题(2015-GX-072);重庆理工大学高等教育教学改革研究项目(2014ZD03);重庆理工大学研究生创新基金资助项目(YCX2015228)
苏理云(1977—),男,四川广安人,博士,副教授,主要从事大数据分析与经济统计研究,E-mail:suliyun@cqut.edu.cn;王杰(1992—),女,河南新乡人,硕士研究生,主要从事金融统计与数据分析研究。
苏理云,王杰.基于SV-POT模型的黄金市场的动态VaR预测[J].重庆理工大学学报(自然科学),2017(5):162-168.
format:SU Li-yun, WANG Jie.VaR Forecasting for Gold Market Based on SV-POT Model[J].Journal of Chongqing University of Technology(Natural Science),2017(5):162-168.
10.3969/j.issn.1674-8425(z).2017.05.027
O21
A
1674-8425(2017)05-0162-07

