主成分分析和因子分析在中国股票评价体系中的应用
胡书文,徐建武
(1.重庆大学 数学与统计学院, 重庆 401331; 2. 92514部队, 山东 烟台 264007)
主成分分析和因子分析在中国股票评价体系中的应用
胡书文1,徐建武2
(1.重庆大学 数学与统计学院, 重庆 401331; 2. 92514部队, 山东 烟台 264007)
目前在中国股票市场上有近3 000只股票,在对股票进行投资之前,需要分析各只股票的盈利情况,从而投资那些盈利能力强、风险小、财务指标好的股票。但股票的评价指标有很多,如何在一个评价体系里考虑所有指标是一个很现实的问题。运用主成分分析和因子分析对中国股票市场进行分析。主成分分析和因子分析能提取出反映股票各方面能力的成分,比如股本扩张能力主成分、盈利能力主成分等,从而可对各股票进行排名,帮助投资者进行决策。
股票评价;主成分分析;因子分析
随着我国股票市场的不断发展,股票投资已成为投资者的主要途径之一。尽管从理论上讲股票投资能给投资者带来收益,甚至是巨大收益,但同时投资者也面临着巨大风险。所以投资者目前的主要目的是在保值的情况下实现最大的增值,这样就有了股票投资分析。当前股票投资分析方法主要有两种:一是基本分析,二是技术分析。但上述分析方法都是定性分析,通常只做一些描述性的说明且带有很强的主观成分,投资者很难从这些主观性的描述中确定哪些是值得投资的股票。因此,如何合理地建立一个投资评价体系成为亟待解决的问题。
2001年S Gnaesalingnaj, KuldeepKumar[1]利用因子分析法,通过对1986—1991年美国证券市场中部分公司的数据进行分析得出了因子分析适合于股票市场的结论。张宗强、任敬喜应用因子分析应用于对2002年度汽车类上市公司投资价值的分析[2]。王文哲、李真燕将因子分析应用于我国家电业上市公司竟争力的分析[3]。顾文炯采用因子分析对农业上市公司进行财务分析[4]。
综上所述,国内外将主成分分析和因子分析应用到股票价值的评价体系中的研究并不是很多,因此本文结合主成分分析和因子分析来对股票进行定量评价,试图得到进一步的结果。
1 评价体系的建立
1.1 指标的选取原则
在建立评价体系时,指标的选取显得尤为重要。不仅要考虑指标反映投资价值的全面性,还要考虑指标体系是否科学、是否具有可比性、是否具有操作性以及数据能否有效得到等许多问题[5]。因此,本文主要考虑以下几个指标选取原则:1) 全面系统原则;2) 恰当适用原则;3) 灵活可控原则;4) 简明科学原则。
1.2 指标的选取
指标的选取对评价体系有很重要的作用[6]。本文选取能反映股票价格的重要财务指标[7]。见表1。
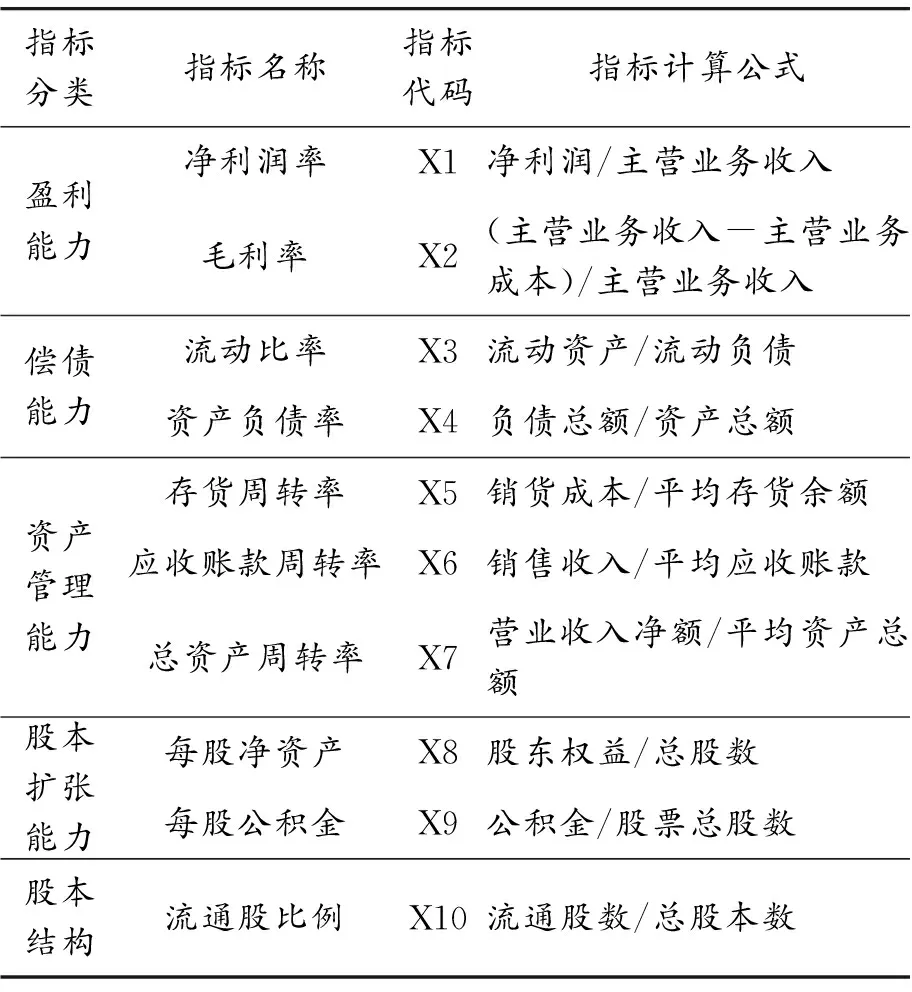
表1 投资价值评价体系指标分类
2 相关统计方法
2.1 主成分分析
主成分分析法就是一种既能保留原有信息又能简化指标变量的多元统计方法,它的目的是降维,设法将原始指标进行综合,求出一组原始指标的线性组合,这些线性组合即为主成分。在这个数学变换中,要求总的方差不变,然后使第一变量的方差最大,即为第一主成分,方差仅次于第一变量且与第一变量独立的第二变量,即为第二主成分,依此类推。在实际应用中,一般提取前几个方差较大的主成分,使其尽可能多地反映原始信息。另外,当主成分个数确定后,可以以各主成分的方差贡献率为权数,构造综合主成分。通过综合主成分的得分得到股票的排名进而构建评价体系。
主成分分析的基本步骤如下[8]:
1) 确认待分析的原有若干变量是否适合做主成分分析,即确定变量之间是否具有较强的相关关系。一般可以做Bartlett球度检验,它是以变量的相关系数矩阵为出发点,零假设是H0:相关系数矩阵是一个单位阵。统计量根据相关系数矩阵的行列式计算得到,如果该统计量值比较大,且其对应的概率值小于某个给定的著性水平,则应拒绝H0,认为相关系数矩阵不太可能是单位阵,适合做主成分分析;反之,则不适合。
2) 对原始指标数据标准化处理,消除计量单位不同量纲不一等因素。设有p个随机变量X1,…,Xp,它们在第i次试验中的取值分别为xi1,xi2,…,xip,其中i=1,…,n。写成矩阵形式有
3) 求出Z的相关系数矩阵R:
4) 求R的特征值和其对应的特征向量:
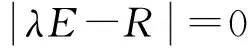
5) 确定主成分个数
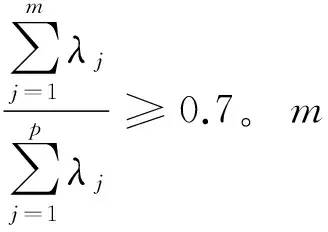
6) 计算综合主成分得分
对m个主成分加权求和,就可以得出综合主成分得分,各主成分的权重通过主成分的方差贡献率来确定。
2.2 因子分析
因子分析是主成分分析的推广,它也是从研究相关系数矩阵内部的关系出发,把一些具有相关关系的变量归结为少数几个综合因子的一种多元统计分析方法。其基本思想是:根据相关性大小将变量分组,使得同组内的变量之间相关性较高,但不同组的变量相关性较低。每组变量代表一个基本结构,这个基本结构称为公共因子。对于所研究的问题就希望用最少个数的不可测的公共因子的线性组合与特殊因子之和来描述原来观测的每一分量。在实际问题中,描述一种现象的指标很多,从一些有关联的现象中找出少数几个主要因子,每一个主要因子就代表一种解释,抓住这些主要因子就可以帮助我们对复杂的问题进行分析和解释。
设X为p×1随机向量, 其均值为μ,协差阵为∑=(σij),若X能表示为X=μ+Af+u,其中∑是p×k未知常数阵,f是k×1随机变量,μ是p×1随机向量, 且
则X=μ+Af+u称为因子分析模型,f称为公共因子,u称为特殊因子。
因子分析的基本步骤如下[9]:
1) 确认待分析的原有若干变量是否适合做因子分析,即确定变量之间是否具有较强的相关关系。一般可以做Bartlett球度检验,具体步骤和上文主成分分析类似。
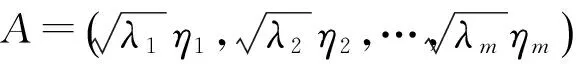
3) 因子变量的命名解释
因子变量的命名解释是因子分析中的重要问题,也是区别于主成分分析的地方。对于上面计算得到的因子载荷矩阵A进行观察,一般会发现这样的现象:A可能在某一行的许多列都有较大的取值,或A可能在某一列的许多行上都有较大取值。这说明:某个原有变量可能同时与几个因子都有比较大的相关关系。因此,可以通过因子旋转的方法使每个变量在尽可能少的因子上有比较高的载荷,即在理想状态下,让某个变量在某个因子上的载荷趋于1,而在其他因子上的载荷趋于0。这样,一个因子就能够成为某个变量的典型代表,实际含义更加清楚。
因子旋转的方法包括正交旋转法、斜交旋转法等,本文分析采用方差极大法。即选取方差最大的正交旋转,将某个因子旋转到某个位置,使每个变量在旋转后的因子轴上的投影向最大、最小两级分化,从而使每个因子中的高载荷只出现在少数的变量上,最后得到的旋转因子载荷矩阵中,每列元素除几个值外,其余的均接近于0。
4) 计算因子得分
得到公共因子和因子载荷后,需要反过来考察每个样本的得分情况,从而对样本进行评价和分类。估计因子得分的方法有很多,如汤普森(Thompson)1939年提出的回归法,也叫汤普森法,约内斯克(Joreskog)和罗莱(Lawley)在1967年提出了一种较为实用的迭代法,R中的因子分析函数factanal就采用了这种算法。
2.3 回归分析
线性回归分析最早由19世纪末期高尔顿提出。线性回归常表示成如下形式:
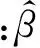
至于回归分析的显著性检验,常见的有F检验和t检验。F检验是对模型的显著性检验,t检验是对系数的显著性检验。
3 评价体系在我国股票市场中的应用
3.1 数据的来源
本文数据来源于2015年10月31日沪深的全部股票,通过西南证券金点子财富管理软件获得2 780只股票,其中沪市1 062只,深市1 718只。
3.2 数据的处理
3.2.1 数据的标准化处理
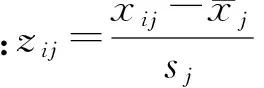
3.3.2 数据的缺失值处理
在实际问题中,有一些数据往往无法获取,进而对整体的数据分析产生影响。所以有必要采取一些方法对缺失值进行处理。常见的方法有:个案剔除法、均值替换法、回归替换法和多重替换法。本文采用剔除法和均值替换法。最后的股票数为2 685只。
3.3 主成分分析
1) 依据上文主成分分析的步骤,首先判断10个变量之间的相关性,相关系数如表2。从表2中可看出:各变量之间的相关系数不是很大。之后做Bartlett球度检验,p值很小,接近0,则应拒绝H0,认为相关系数矩阵不太可能是单位阵,适合做主成分分析。
2) 用R中的函数scale()对原始数据进行标准化[10]
3) 求标准化后数据的特征值
10个特征值依此为:5 158.753 3,3 333.053 2,2 786.389 5,2 734.092 8,2 694.469 0,2 640.575 7,2 524.126 4,2 335.578 3,1 804.966 5,827.995 4。 4) 直接使用R提供的主成分函数princomp()进行主成分分析,结果分别见图1, 2, 3。
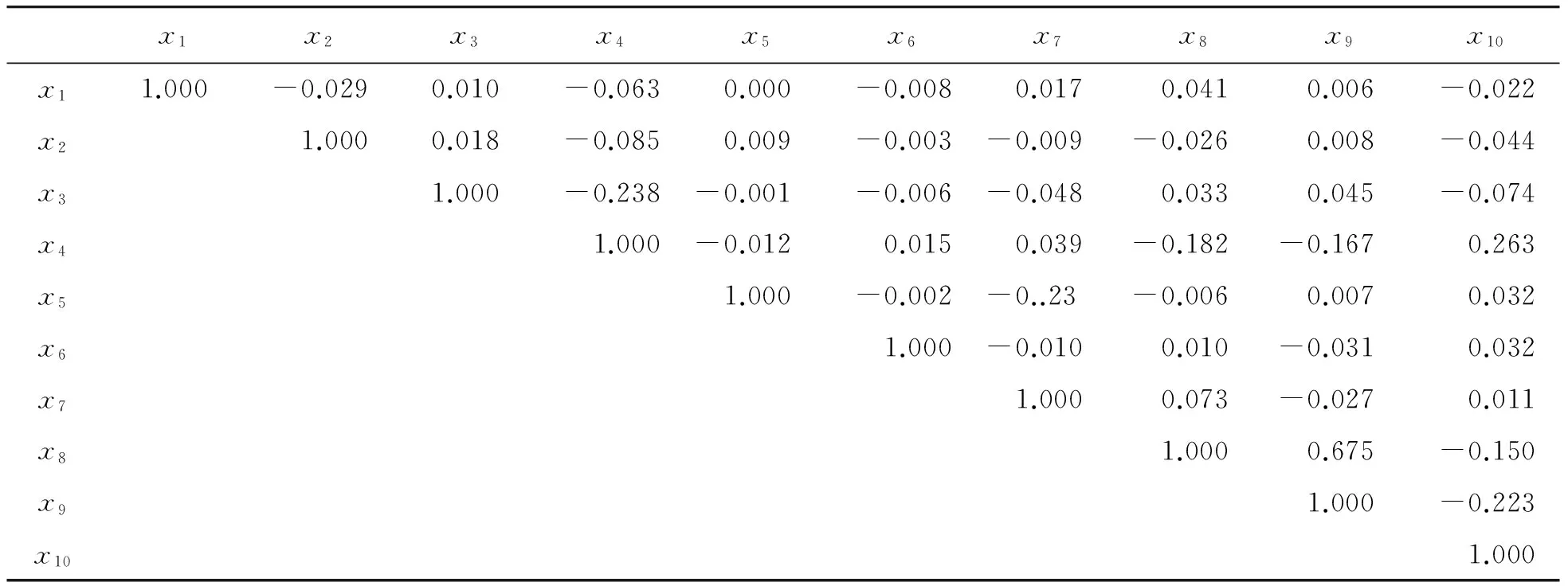
表2 相关系数矩阵

图1 主成分分析结果
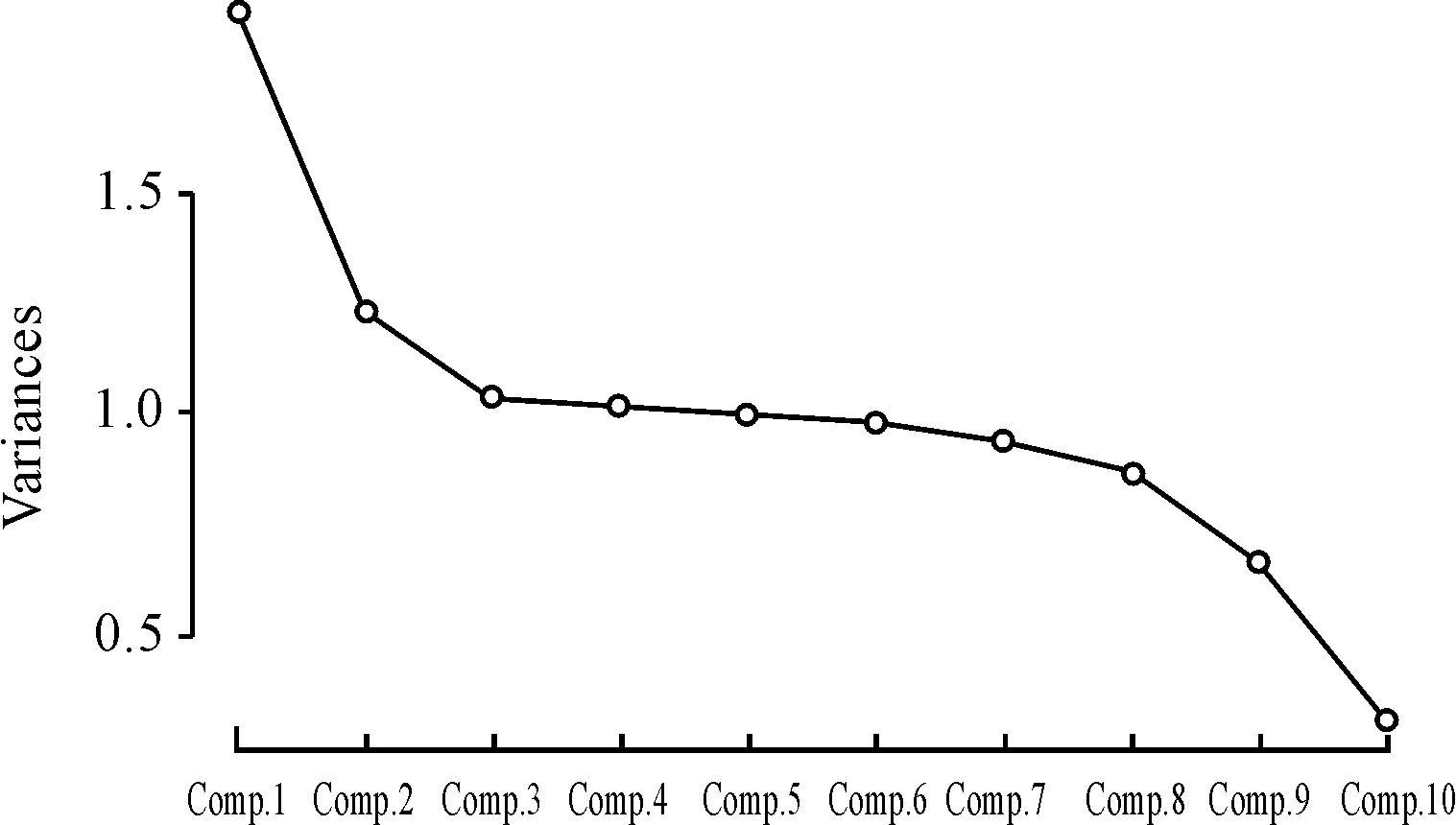
图2 主成分碎石图
由图1知:前6个主成分的方差之和占全部方差之和的72%,所以按照本文标准选6个主成分为宜。这样,原来的10个指标转化成6个,起到了降维的作用。且由主成分碎石图可以看出:前3个主成分解释的原始信息较多,第5主成分到第6主成分没有明显的下降趋势,但前5个主成分的方差之和只占全部方差之和的62%,所以还是选前6个主成分。
第1主成分Y1=0.18x3-0.38x4+0.58x8+0.59x9-0.37x10
第2主成分Y2=0.3x2+0.53x3-0.49x4-0.29x7-0.37x8-0.31x9-0.26x10
第3主成分Y3=0.65x1-0.31x2-0.1x4-0.41x5-0.24x6+0.45x7-0.16x9-0.1x10
第4主成分Y4=-0.43x1+0.53x2-0.18x3-0.5x5-0.29x6+0.36x7-0.2x10
第5主成分Y5=-0.12x1-0.13x2+0.13x3-0.58x5+0.78x6
第6主成分Y6=0.29x1+0.5x2-0.1x3+0.39x5+0.47x6+0.51x7
第1主成分方差贡献率为19.22%,主要与每股净资和每股公积有关,这2个指标能衡量股本的扩张能力,称为股本扩张能力主成分;第2主成分方差贡献率为12.42%,主要与流动比率和资产负债率有关,而这2个指标可衡量偿债能力,称为偿债能力主成分;第三主成分方差贡献率为10.38%,主要与净利润率有关,但其他各方面也都涵盖,把它称为综合主成分;第4主成分方差贡献率为10.19%,主要与净利润率和毛利率有关,这2个指标能衡量盈利能力,称为盈利能力主成分;第5主成分方差贡献率为10.04%,主要与存货周转率和总应收账款周转率有关,可衡量资产管理能力,称为资产管理能力主成分;第6主成分方差贡献率为9.8%,主要与毛利率和总资产周转率有关,叫做盈利能力和资产管理能力主成分[11]。
5) 令第1主成分Y1,第2主成分Y2,第3主成分Y3,第4主成分Y4,第5主成分Y5,第6主成分Y6为自变量,现价Y为因变量,做回归分析。其中R2=0.3012,调整的R2=0.2996,说明拟合优度不是很好,但p值很小,说明模型通过了检验。Y=20.76+6.51Y1+0.03Y2+0.1Y3+0.84Y4-0.27Y5+1.08Y6,而Y2,Y3和Y5的系数没有通过检验,猜测可能是自变量之间存在着严重的相关性,因为Y3被命名为综合主成分,所以和其他主成分之间存在交叉。
然后采用逐步回归法,利用R中的step( )函数,该函数以AIC信息量为准则,默认的是向后法,从所有变量开始,逐步通过选择最小的AIC信息量达到增删变量的目的。结果最后保留的变量是第1主成分Y1,第4主成分Y4,第6主成分Y6,回归方程为Y=20.76+6.51Y1+0.84Y4+1.08Y6,且系数也都通过了显著性检验。说明股价主要和第1主成分股本扩张能力主成分、第4主成分盈利能力主成分、第6主成分盈利能力和资产管理能力主成分有关,这也符合实际情况。
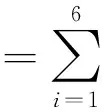
限于篇幅,这里只给出了排名前20名和后20名的股票。本文的评价系统对每个股票的评价具有现实的参考价值。
3.4 因子分析
1) 按照上述因子分析的步骤,首先确认原有若干变量是否适合做因子分析,即是否具有相关性,根据主成分分析的结果,答案是肯定的。
2)构造因子变量和计算因子载荷矩阵
因子分析和主成分分析有一个不同之处在于主成分分析是根据算出来的累积贡献率来确定主成分个数,但是因子分析是在之前就预判出要提取的因子个数。此处采用R中的 fa.parallel函数,结果建议选择3个因子,如图4。但3个因子总的方差贡献率仅为42%,为防止遗漏重要信息,选取5个因子。5个因子的方差贡献率为62.2%。
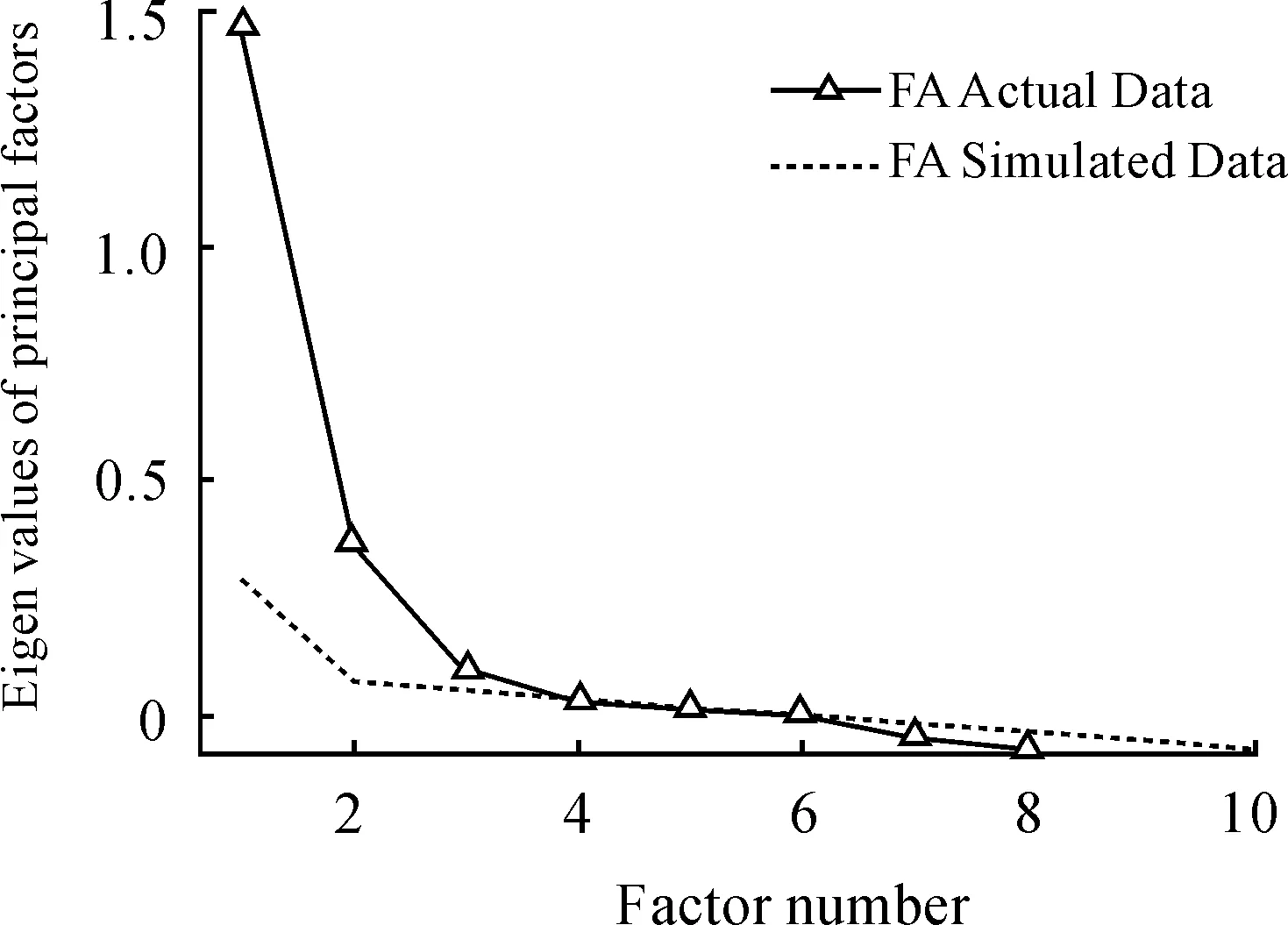
图4 因子选取
3) 因子变量的命名解释,因子载荷矩阵见表4。
由表4可以看出:尽管一个因子可以解释许多变量信息,但它却只能解释某个变量的少部分信息,不是任何一个变量的典型代表。这样的情况必然使得因子变量的实际含义模糊不清。因此,可以通过因子旋转的方法使每个变量在尽可能少的因子上有比较高的载荷。这样,一个因子就能够成为某个变量的典型代表,实际含义更加清楚。这里采用方差极大法进行因子旋转。旋转后的因子载荷矩阵见表5。
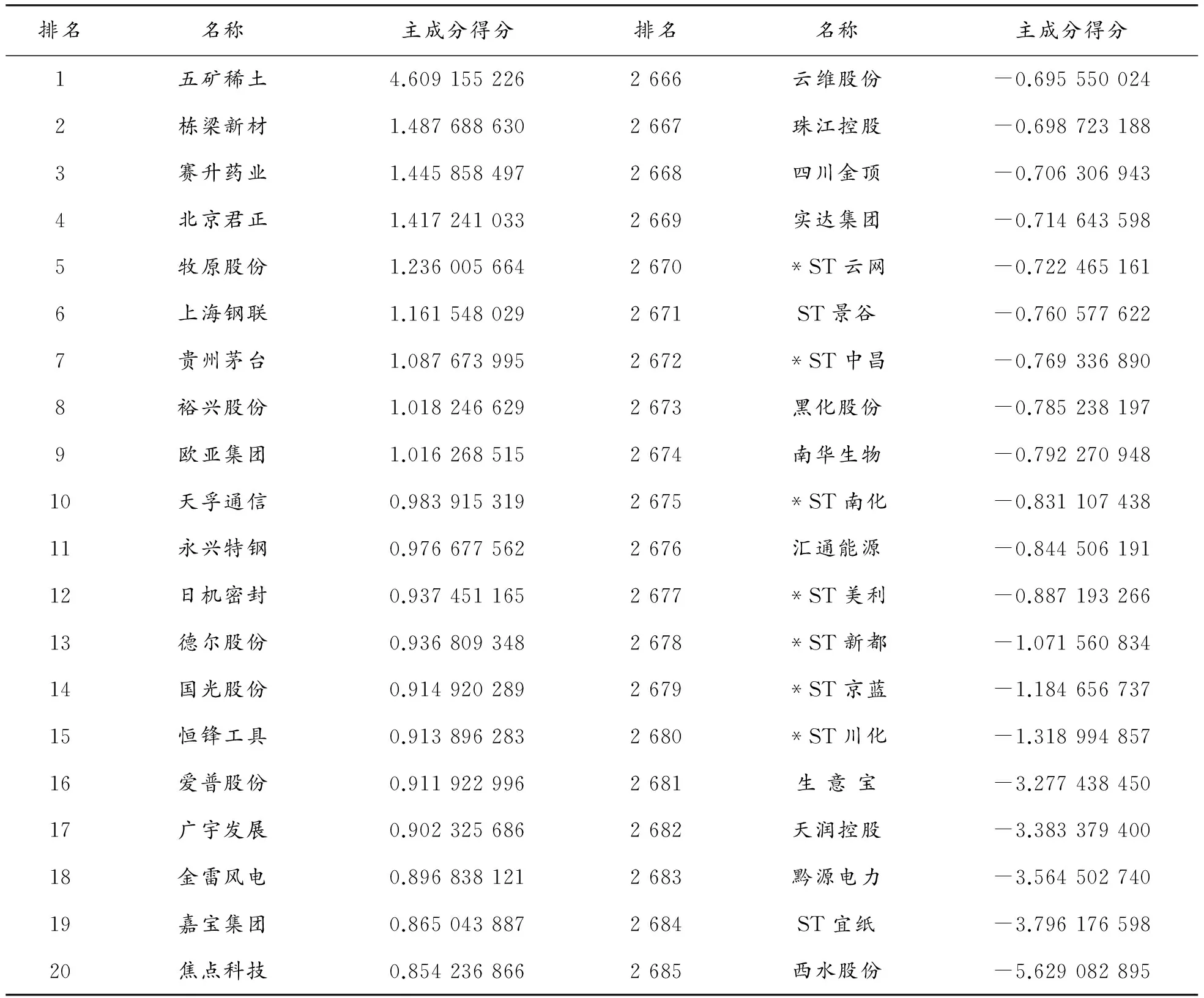
表3 主成分得分排名
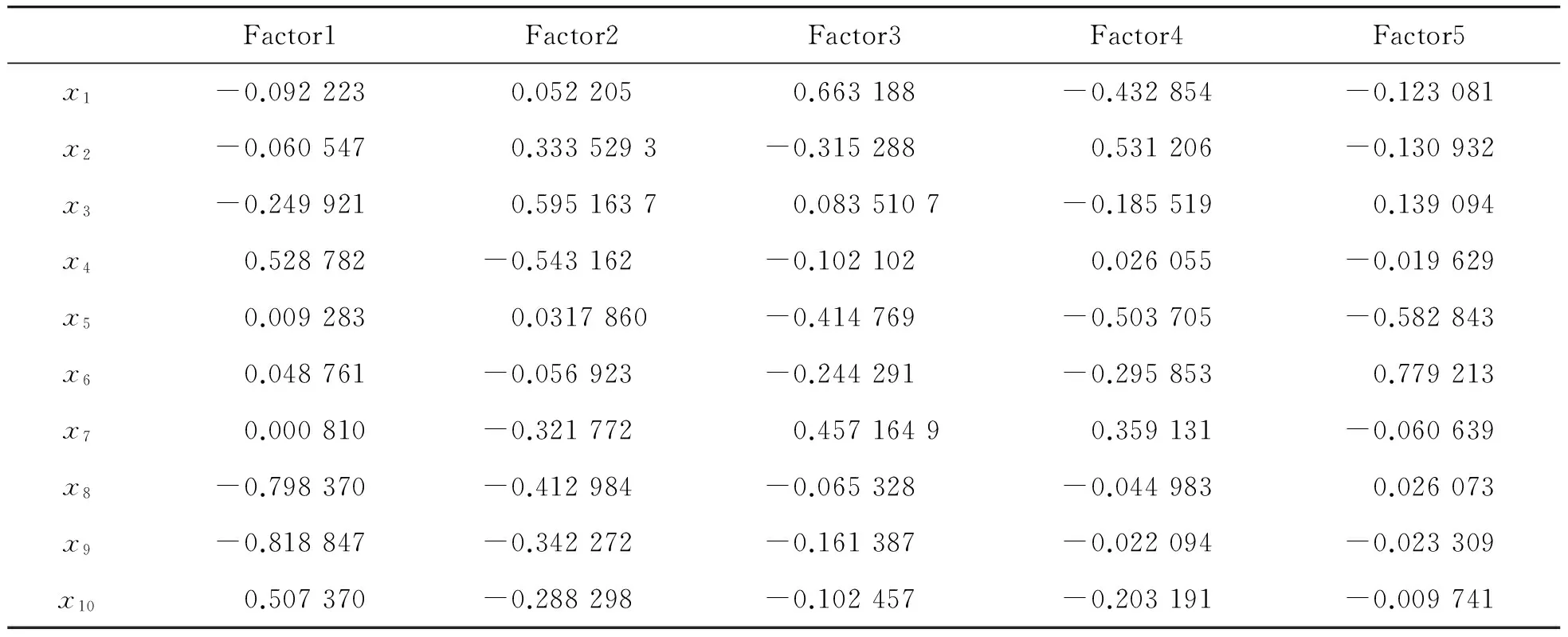
表4 因子载荷矩阵
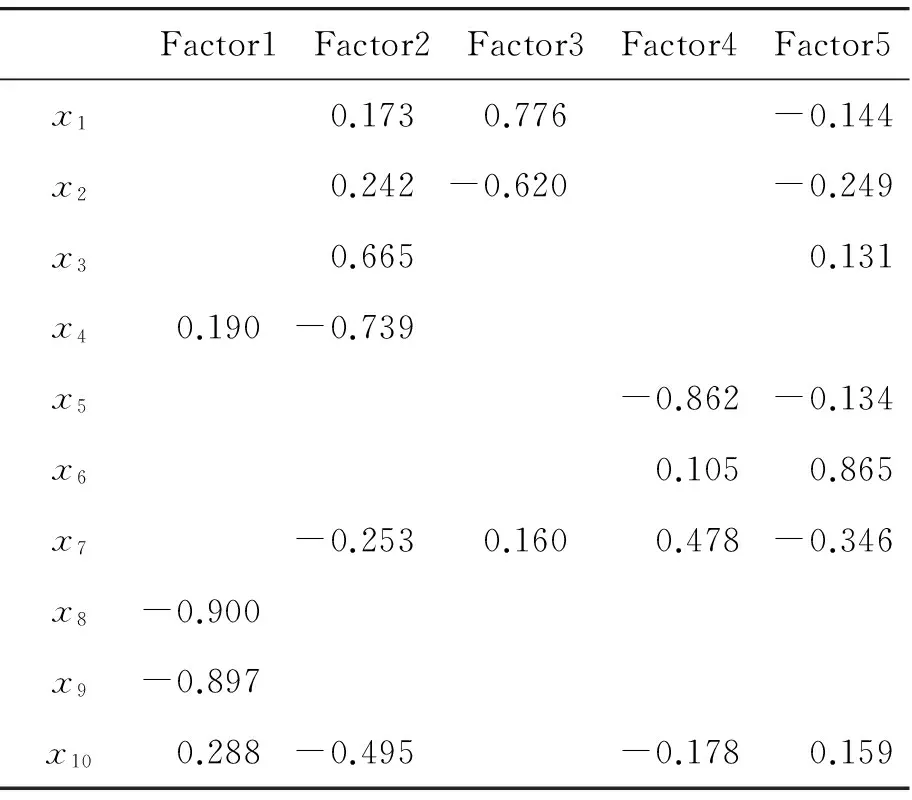
表5 旋转后的因子载荷矩阵
每股净资产x8,每股公积金x9在Factor1上有较大载荷,称为股本扩张能力因子;流动比率x3,资产负债率x4,流通股比例x10在Factor2上有较大载荷,称为偿债能力因子和股本结构因子;净利润率x1,毛利率为x2在Factor3上有较大载荷,称为盈利能力因子;存货周转率x5,总资产周转率x7在Factor4上有较大载荷,称为资产管理能力因子;应收账款周转率x6在Factor5上有较大载荷,称为资产管理能力因子。
4) 计算因子得分
用R中的因子分析函数factanal计算因子得分,然后以各因子的方差贡献率为权数,算出总的因子得分并进行排名。见表6。
与前面的主成分得分排名进行对比发现:主成分得分排名第1的五矿稀土在因子得分中排名倒数第7,而查看五矿稀土的具体情况不难看出其综合主成分得分为4.61,明显高于后面股票的综合主成分,原因在于它的第2主成分显著较高,而第2主成分为偿债能力主成分,并非越高越好,而是需要在一个合适的范围。且因子得分中五矿稀土的得分比较低是因为第5因子资产管理能力因子特别低,即应收账款周转率特别低,说明企业的资金周转不好,所以综合来看,虽然五矿稀土的主成分得分排名第1,但是不推荐。
因此,考虑把主成分得分和因子得分综合起来考虑,取平均值,得到的最终排名如表7(排除五矿稀土和西水股份,因为其主成分得分明显异常),明显看出排名较差的20名中有好多是ST板块的,也比较符合实际情况。搜索了一下排名靠前的股票,例如上海钢联、贵州茅台和赛升药业等,也都是利好消息,可以投资。例如上海钢联排名第一,查阅相关信息可知[12]:上海钢联在国内钢铁工业陷入严冬之际,主营线上钢市信息和钢材交易,在过去一段时间里实现了股价十几倍的暴涨。这家公司在2011年登陆创业板,此前主营业务是钢铁行业的咨询信息服务。在传统钢贸业企业纷纷倒塌的时候,该公司开始向后端的线上交易、金融等板块延伸,意在打造垂直于钢铁全产业链条的电商生态系统。被贴上互联网、金融、电商标签的上海钢联迅速成为资本市场的宠儿。从2013年的5月到2015年的3月,股价从8元左右飙升至143元左右,涨超16倍。2015年9月到12月,该股的关注度高于行业内的其他113家公司,排名第41。共有5家机构发布了18篇关于该股的研究报告,该股综合评级为增持,维持前期评级。虽然截止目前(2016年1月8日)的消息[13]是:上海钢联跌停,报于36.38元,但其实是跟这些天股市的不稳定形态有关[14],在熔断机制运行的4个交易日中已有1月4日和1月7日两天被触发熔断,同时均伴随市场暴跌。1月4日下午,A股大跌连续两次触发熔断并暂停交易;3天后,沪深300指数在开盘不到半小时内,再度两次触发熔断。实施熔断机制连续4天以来,上证指数跌幅累计达11.96%。所以,这不影响上海钢联的内在投资价值。排名最后的ST宜纸本身就处于ST板块,且最新的消息是“ST宜纸‘易主+重组’方案遭上交所问询”,也已停牌多日,显然不适合投资。
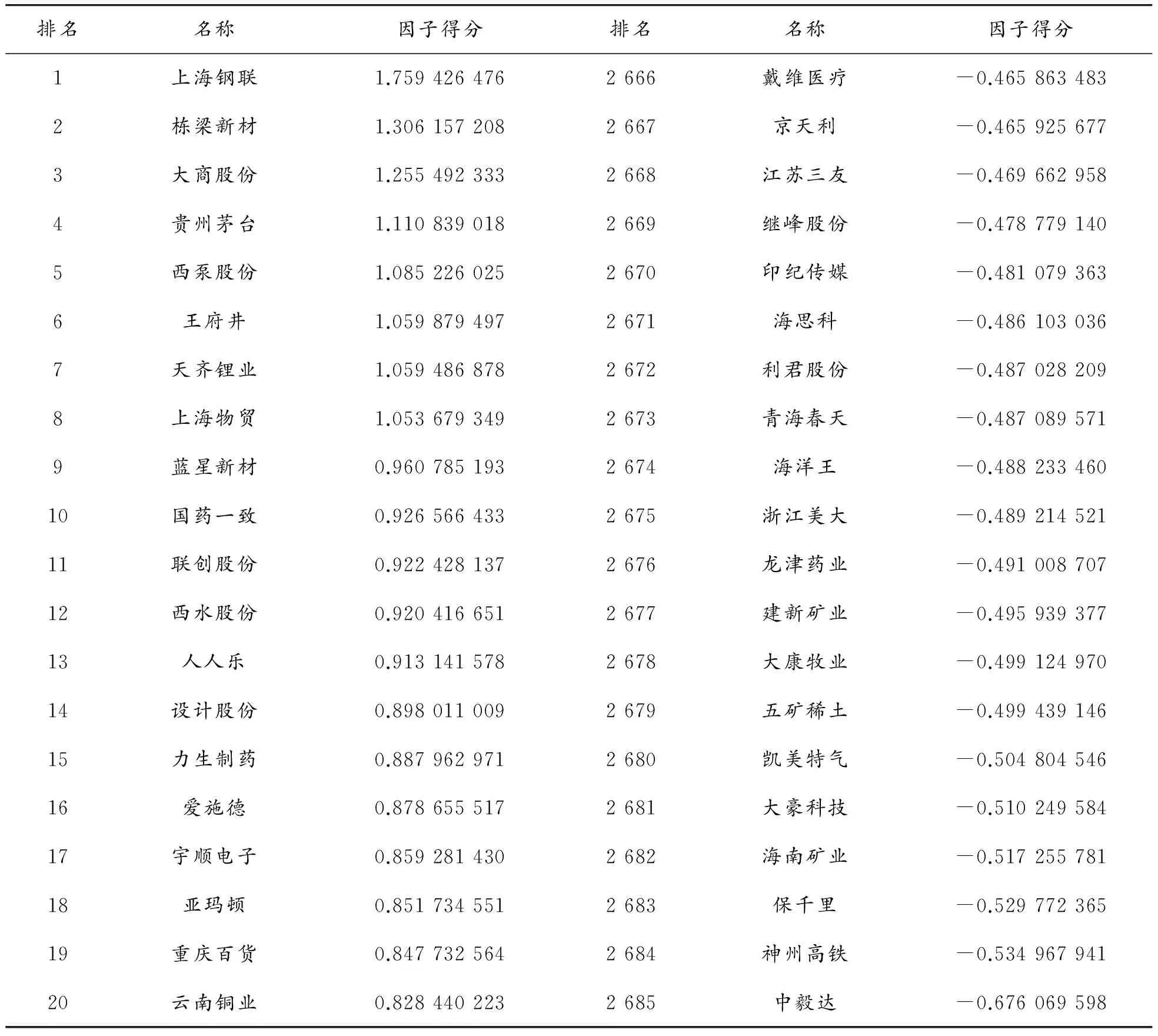
表6 因子得分排名

表7 综合排名
4 结论与展望
4.1 主要结论
本文分析了影响股票的一些重要财务指标,利用主成分分析和因子分析建立了股票的评价体系,并利用相关数据分析得出影响股价最重要的因素有股本扩张能力、盈利能力和资产管理能力,给出了一个最终的股票排名。表7是根据这个评价体系给出的股票投资的参考。
4.2 展望
本文所提出的投资评价体系仍然存在不足之处。例如指标的选取不全,没有考虑到影响股票的其他宏观因素、数据的选取问题等。总之,要更加透彻地研究股票评价模型,不仅需要进一步深化学习,还应该努力追踪国内外最新研究进展,通过对股票影响因素的深入挖掘,结合我国股票变化特点,形成一套行之有效的理论。
[1] GAMESALINGAM S,KUMAR K.Detection of financial distress via multivariate statistical analysis[J].Managerial Finance,2001,27(4):45-55.
[2] 张宗强,任敬喜.对2002年度汽车类上市公司投资价值的因子分析[J].价值工程,2004(5):109-112.
[3] 王文哲,李真燕.我国家电上市公司竞争力的因子分析[J].价值工程,2005(3):105-108.
[4] 顾文炯.用因子分析对农业上市公司进行财务评价[J].安徽大学学报,2005,29(3):136-139.
[5] 杜茜,张雪梅.清洁能源行业上市公司投资价值评估研究[D].北京:中国地质大学,2013.
[6] 任福匀.因子分析法在我国股票市场行业投资价值评价中的应用[D].长沙:中南大学,2005.
[7] 姜爱宇.部分线性模型在股票价格预测中的应用研究[D].大连:辽宁师范大学,2012.
[8] 王学民.应用多元分析[M].上海:上海财经大学出版社,2009.
[9] 杨虎.金融大数据统计方法与实证[M].北京:科学出版社,2016.
[10]汤银才.R语言与统计分析[M].北京:高等教育出版社,2008:316-324.
[11]张甜,牛明飞.基于主成分分析的股价因素分析[D].兰州:兰州大学,2013.
[12]新京报.上海钢联:从8元涨到143元的“电商故事”[EB/OL].[2015-04-13].http://tech.163.com/15/0413/02/AN22CJ0700094ODV.html.
[13]金融界网站.快讯:上海钢联跌停 报于36.38元[EB/OL].[2016-01-08].http://stock.jrj.com.cn/hotstock/2016/01/08095720376470.shtml.
[14]东方网.熔断重启时间未定证监会称将“不断完善相关机制”[EB/OL].[2016-01-08].http://finance.sina.com.cn/roll/2016-01-08/doc-ifxnkeru4776113.shtml.
(责任编辑 陈 艳)
Application of Principal Component Analysis and Factor Analysis in China’s Stock Evaluation Market
HU Shu-wen1, XU Jian-wu2
(1.College of Mathematical and Statistics, Chongqing University, Chongqing 401331, China;2.The No.92514thTroop of PLA, Yantai 264007, China)
At present, there are nearly 3 000 stocks in the Chinese stock market. Before entering in the stock market, it is necessary to analyze the profitability of each stock and invest in that stocks with strong profitability, low risk and good financial indicators. However, there are many evaluation indicators of the stocks and how to evaluate all the indicators systematically is a very important problem. China’s stock market was analyzed by principal component analysis and factor analysis. These two measures can extract the components that reflect the various aspects of the stock, such as the principal component of capital expansion capacity, principal component of profitability, and so on. After getting the principal component scores and factor scores, the stocks whose ranks were relatively high and low were analyzed and it is perfect to meet the actual situation. So the final ranks were given after considering the two cases.
stock evaluation; principal component analysis; factor analysis
2016-12-17 基金项目:国家自然科学基金青年基金资助项目(11001286)
胡书文(1992—),女,硕士研究生,主要从事纵向数据、线性模型方面的研究,E-mail:swhu@cqu.edu.cn。
胡书文,徐建武.主成分分析和因子分析在中国股票评价体系中的应用[J].重庆理工大学学报(自然科学),2017(5):192-202.
format:HU Shu-wen, XU Jian-wu.Application of Principal Component Analysis and Factor Analysis in China’s Stock Evaluation Market[J].Journal of Chongqing University of Technology(Natural Science),2017(5):192-202.
10.3969/j.issn.1674-8425(z).2017.05.032
O212.4;F830.91
A
1674-8425(2017)05-0192-11

