关于不定方程x2+4n=y15(n=1,2,3)的整数解

尚 旭,王泽灯

(浙江师范大学 数理与信息工程学院,浙江 金华 321000)

【自然科学基础理论研究】

关于不定方程x2+4n=y15(n=1,2,3)的整数解

尚 旭,王泽灯

(浙江师范大学 数理与信息工程学院,浙江 金华 321000)

不定方程整数解的问题是数论方面的一个重要问题。利用代数数论和同余理论的方法,研究不定方程x2+4n=y15(x,y∈Z)的整数解问题，并证明了不定方程x2+4n=y15(n=1，2，3)无整数解。

不定方程;整数解;代数数论

0 引言

不定方程[1]是数论的一个重要分支,它有着丰富的内容和悠久的历史。不定方程一般是指未知数的个数多于方程的个数,其最早可追溯到3世纪初，当时古希腊数学家丢番图研究过许多这样的方程,因此不定方程又称丢番图方程。不定方程与代数数论、几何数论、集合数论等有着密切的联系，在有限群论和最优设计中也常常提出不定方程的问题,这就使得不定方程这一古老的分支继续吸引着许多数学家的关注,成为数论中重要的研究课题之一。

设A，B∈N,A无平方因子,关于不定方程

Ax2+B=yn(x,y,n∈N,n≥2)

(1)

解的问题是数论中的一个重要问题,用初等方法解决此类问题比较复杂和困难。近些年许多研究者用代数数论的方法研究了许多形式的不定方程:Ledesgue[2]证明了当A=1,B=1时,(1)式无整数解；Nagell[3]证明了当A=2,B=1,n=5时,仅有整数解(x,y)=(±11,3)；孙树东[4]证明了当A=1,B=64,n=13时无整数解；杨全[5]证明了当A=1,B=16,n=9时无整数解；李中恢、张四保[6]证明了当A=1,B=16,n=11时无整数解；张杰[7]证明了当A=1,B=64,n=7时无整数解,而对于n=15未曾研究。基于此,本文研究当A=1,B=4,16,64,n=15时方程x2+4n=y15(n=1,2,3)的整数解问题。

引理1[8]设M是唯一分解整数环,正整数k≥2,以及α,β∈Z,(α,β)=1，αβ=τk,τ∈M,则有α=ε1μk,β=ε2νk,μ,ν∈M,其中：ε1,ε2是M中的单位元素,并且ε1ε2=εk,ε为单位元素。

1 主要结果及证明

定理1 不定方程

x2+4=y15,x,y∈Z

(2)

无整数解。

证明 分两种情况说明：

(1)x≡1(mod 2)，则在Z[i]中,(2)式可以等价写成(x+2i)(x-2i)=y15,x,y∈Z。

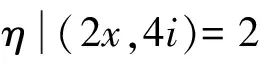
由此和引理1有

x+2i=(a+bi)15，x,a,b∈Z。

因此得

x=a15-105a13b2+1 365a11b4-5 005a9b6+6 435a7b8-3 003a5b10+455a3b12-15ab14，

(3)

2=b(15a14-455a12b2+3 003a10b4-6 435a8b6+5 005a6b8-1 365a4b10+105a2b12-b14)。

(4)

因此b=±1,±2。

当b=1时，由(4)式得

2=15a14-455a12+3 003a10-6 435a8+5 005a6-1 365a4+105a2-1，

3=15a14-455a12+3 003a10-6 435a8+5 005a6-1 365a4+105a2，

即3=a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105)。

(5)

(5)式要成立,则a2=1。

代入(5)式,有

a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105)=-127≠3，

所以b=1不成立。

当b=-1时，由(4)式得

-2=15a14-455a12+3 003a10-6 435a8+5 005a6-1 365a4+105a2-1，

-1=15a14-455a12+3 003a10-6 435a8+5 005a6-1 365a4+105a2，

即-1=a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105)。

(6)

(6) 式要成立,则a2=1。

代入(6)式，有

a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105)=-127≠-1，

所以b=-1不成立。

当b=2时，由(4)式得

1=15a14-1 820a12+48 048a10-411 840a8+1 281 280a6-1 397 760a4+430 080a2-214，

214+1=15a14-1 820a12+48 048a10-411 840a8+1 281 280a6-1 397 760a4+430 080a2，

16 385=5×29×113=

a2(15a12-1 820a10+48 048a8-411 840a6+1 281 280a4-1 397 760a2+430 080)。

(7)

(7) 式要成立,则a2=1。

代入(7)式,有

a2(15a12- 1 820a10+48 048a8-411 840a6+1 281 280a4-1 397 760a2+430 080)

=-51 997≠16 385，

所以b=2不成立。

当b=-2时，由(4)式得

-1=15a14-1 820a12+48 048a10-411 840a8+1 281 280a6-1 397 760a4+430 080a2-214，

214-1=15a14-1 820a12+48 048a10-411 840a8+1 281 280a6-1 397 760a4+430 080a2，

16 383=3×43×127=

a2(15a12-1 820a10+48 048a8-411 840a6+1 281 280a4-1 397 760a2+430 080)。

(8)

(8) 式要成立,则a2=1。

代入(8)式,有

a2(15a12- 1 820a10+48 048a8-411 840a6+1 281 280a4-1 397 760a2+430 080)

=-51 997≠16 383，

所以b=-2不成立。

所以当x≡1(mod 2)时,不定方程x2+4=y15无整数解。

(2)x≡0(mod 2)。x为偶数,易知y也是偶数,令x=2x1，y=2y1，x1,y1∈Z。此时(2)式等价为

(2x1)2+4=(2y1)15，

即

x12+1=213y115。

(9)

由(9)式易知x1为奇数,可令x1=2x2+1,x2∈Z，代入(9)式得(2x2+1)2+1=213y115，整理得

2x22+2x2+1=212y115。

(10)

由(10)式知左边2x22+2x2+1≡1(mod 2),而右边212y115≡0(mod 2)，则产生矛盾。

所以当x≡0(mod 2)时,不定方程x2+4=y15无整数解。

综上,不定方程x2+4=y15(x,y∈Z)无整数解。

定理2 不定方程

x2+16=y15(x,y∈Z)

(11)

无整数解。

证明 分两种情况说明：

(1)x≡1(mod 2)，则在Z[i]中,(11)式可以等价写成(x+4i)(x-4i)=y15,x,y∈Z。

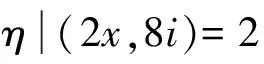
由此和引理1有

x+4i=(a+bi)15，x,a,b∈Z。

(12)

因此得

x=a15-105a13b2+1 365a11b4-5 005a9b6+6 435a7b8-3 003a5b10+455a3b12-15ab14，

(13)

4=b(15a14-455a12b2+3 003a10b4-6 435a8b6+5 005a6b8-1 365a4b10+105a2b12-b14)。

(14)

因此b=±1,±2,±4。

当b=1时，由(14)式得

4=15a14-455a12+3 003a10-6 435a8+5 005a6-1 365a4+105a2-1，

5=15a14-455a12+3 003a10-6 435a8+5 005a6-1 365a4+105a2，

5=a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105)。

(15)

(15)式要成立,则a2=1。

代入(15)式,有

a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105)=-127≠5，

所以b=1不成立。

当b=-1时，由(14)式得

-4=15a14-455a12+3 003a10-6 435a8+5 005a6-1 365a4+105a2-1，

-3=a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105) 。

(16)

(16)式要成立,则a2=1。

代入(16)式，有

a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105)=-127≠-3，

所以b=-1不成立。

当b=2时,由(14)式得

2= 15a14-455a12×22+3 003a10×24-6 435a8×26+5 005a6×28-

1 365a4×210+105a2×212-214，

214+2= 15a14-455a12×22+3 003a10×24-6 435a8×26+5 005a6×28-

1 365a4×210+105a2×212。

16 386= 2×3×2731=a2(15a12-455a10×22+3 003a8×24-6 435a6×26+

5 005a4×28-1 365a2×210+105×212)。

(17)

(17)式要成立,则a2=1。

代入(17)式，有

所以b=2不成立。

当b=-2时，由(14)式得

-2= 15a14-455a12×(-2)2+3 003a10×(-2)4-6 435a8×(-2)6+5 005a6×(-2)8-

1 365a4×(-2)10+105a2×(-2)12-(-2)14，

214-2= 15a14-455a12×22+3 003a10×24-6 435a8×26+5 005a6×28-

1 365a4×210+105a2×212,

16 382= 2×8191=a2(15a12-455a10×22+3 003a8×24-6 435a6×26+5 005a4×28-

1 365a2×210+105×212)。

(18)

(18)式要成立,则a2=1。

代入(18)式,有

a2(15a12-455a10×22+3 003a8×24-6 435a6×26+5 005a4×28-1 365a2×210+105×212)

=-51 997≠16 382，

所以b=-2不成立。

当b=4时，由(14)式得

1= 15a14-455a12×42+3 003a10×44-6 435a8×46+5 005a6×48-

1 365a4×410+105a2×412-414，

414+1= 15a14-455a12×42+3 003a10×44-6 435a8×46+5 005a6×48-

1 365a4×410+105a2×412。

268 435 457= 17×15 790 321=a2(15a12-455a10×42+3 003a8×44-6 435a6×46+5 005a4×48-

1 365a2×410+105×412)。

(19)

(19)式要成立,则a2=1。

代入(19)式,有

a2(15a12-455a10×42+3 003a8×44-6 435a6×46+5 005a4×48-1 365a2×410+105×412)

=632 712 863≠268 435 457，

所以b=4不成立。

当b=-4时，由(14)式得

-1= 15a14-455a12×(-4)2+3 003a10×(-4)4-6 435a8×(-4)6+5 005a6×(-4)8-

1 365a4×(-4)10+105a2×(-4)12-(-4)14，

414-1= 15a14-455a12×42+3 003a10×44-6 435a8×46+5 005a6×48-

1 365a4×410+105a2×412。

268 435 455= 3×5×29×43×113×127=a2(15a12-455a10×42+3 003a8×44-

6 435a6×46+5 005a4×48-1 365a2×410+105×412)。

(20)

(20)式要成立,则a2=1。

代入(20)式,有

a2(15a12- 455a10×(-4)2+3 003a8×(-4)4-6 435a6×(-4)6+5 005a4×(-4)8-

1 365a2×(-4)10+105×(-4)12)=632 712 863≠268 435 455，

所以b=-4不成立。

所以,当x≡1(mod 2)时,不定方程x2+16=y15无整数解。

(2)x≡0(mod 2)，x为偶数,易知y也是偶数,令x=2x1，y=2y1，x1,y1∈Z，此时(11)式等价为

(2x1)2+16=(2y1)15，

即

x12+4=213y115。

(21)

由(21)式易知x1为偶数,则可令x1=2x2,x2∈Z，代入(21)式得(2x2)2+4=213y115，整理得

x22+1=211y115。

(22)

由(22)式知x2为奇数,则令x2=2x3+1,x3∈Z，

(2x3+1)2+1=211y115，

即

2x32+2x3+1=210y115。

(23)

由(23)式知左边2x32+2x3+1≡1(mod 2),而右边210y115≡0(mod 2),则产生矛盾。

所以，当x≡0(mod 2)时,不定方程x2+16=y15无整数解。

综上,不定方程x2+16=y15(x,y∈Z)无整数解。

定理3 不定方程

x2+64=y15(x,y∈Z)

(24)

无整数解。

证明 分两种情况说明：

(1)x≡1(mod 2)，则在Z[i]中,(24)式可以等价写成(x+8i)(x-8i)=y15,x,y∈Z。

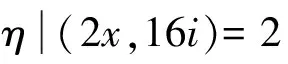
由此和引理1有

x+8i=(a+bi)15，x,a,b∈Z。

(25)

因此得

x=a15-105a13b2+1 365a11b4-5 005a9b6+6 435a7b8-3 003a5b10+455a3b12-15ab14，

(26)

8=b(15a14-455a12b2+3 003a10b4-6 435a8b6+5 005a6b8-1 365a4b10+105a2b12-b14)。

(27)

因此b=±1,±2,±4,±8。

当b=1时,由(27)式得

8=15a14-455a12+3 003a10-6 435a8+5 005a6-1 365a4+105a2-1，

9=a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105) 。

(28)

(28)式要成立,则a2=1或a2=9。

当a2=1时,代入(28)式,有

a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105)=-127≠9，

所以a2=1不成立。

当a2=9时，代入(28)式,有

a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105)=-31 417 983≠9，

所以a2=9不成立。

所以b=1不成立。

当b=-1时,由(27)式得

-8=15a14-455a12+3 003a10-6 435a8+5 005a6-1 365a4+105a2-1，

-7=a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105) 。

(29)

(29)式要成立,则a2=1。

代入(29)式，有

a2(15a12-455a10+3 003a8-6 435a6+5 005a4-1 365a2+105)=-127≠-7，

所以b=-1不成立。

当b=2时，由(27)式得

4= 15a14-455a12×22+3003a10×24-6 435a8×26+5 005a6×28-

1 365a4×210+105a2×212-214，

214+4=a2(15a12-455a10×22+3 003a8×24-6 435a6×26+5 005a4×28-

1 365a2×210+105×212)，

16 388= 4×17×241=a2(15a12-455a10×22+3 003a8×24-6 435a6×26+

5 005a4×28-1 365a2×210+105×212)。

(30)

(30)式要成立,则a2=1或a2=4。

当a2=1时,代入(30)式，有

a2(15a12- 455a10×22+3 003a8×24-6 435a6×26+5 005a4×28-1 365a2×210+105×212)

=-51 997≠16 388，

所以a2=1不成立。

当a2=4时，代入(30)式,有

a2(15a12- 455a10×22+3 003a8×24-6 435a6×26+5 005a4×28-1 365a2×210+105×212)

=-2 080 768≠16 388，

所以a2=4不成立。

所以b=2时不成立。

当b=-2时，由(27)式得

-4 =15a14-455a12×(-2)2+3 003a10×(-2)4-6 435a8×(-2)6+5 005a6×(-2)8-

1 365a4×(-2)10+105a2×(-2)12-(-2)14，

214-4= 15a14-455a12×22+3 003a10×24-6 435a8×26+5 005a6×28-

1 365a4×210+105a2×212,

16 380= 4×5×7×9×13=a2(15a12-455a10×22+3 003a8×24-6 435a6×26+

5 005a4×28-1 365a2×210+105×212)。

(31)

(31)式要成立,则a2=1,a2=4,a2=9,a2=36。

当a2=1时,代入(31)式,有

a2(15a12-455a10×22+3 003a8×24-6 435a6×26+5 005a4×28-1 365a2×210+105×212)

=-51 997≠16 380，

所以a2=1不成立。

当a2=4时,代入(31)式，有

a2(15a12- 455a10×22+3 003a8×24-6 435a6×26+5 005a4×28-1 365a2×210+105×212)

=-2 080 768≠16 380，

所以a2=4不成立。

当a2=9时,代入(31)式，有

a2(15a12- 455a10×22+3 003a8×24-6 435a6×26+5 005a4×28-1 365a2×210+105×212)

=64 331 307≠16 380，

所以a2=9不成立。

当a2=36时,代入(31)式

a2(15a12- 455a10×22+3 003a8×24-6 435a6×26+5 005a4×28-1 365a2×210+105×212)

=-514 752 233 472≠16 380，

所以a2=36不成立。

所以b=-2不成立。

当b=4时，由(27)式得

2= 15a14-455a12×42+3 003a10×44-6 435a8×46+5 005a6×48-

1 365a4×410+105a2×412-414，

414+2= 15a14-455a12×42+3 003a10×44-6 435a8×46+5 005a6×48-

1 365a4×410+105a2×412，

268 435 458= 2×34×19×87 211=a2(15a12-455a10×42+3 003a8×44-

6 435a6×46+5 005a4×48-1 365a2×410+105×412)。

(32)

(32)式要成立,则a2=1,a2=9,a2=81。

当a2=1时,代入(32)式有

a2(15a12- 455a10×42+3 003a8×44-6 435a6×46+5 005a4×48-1 365a2×410+105×412)

=632 712 863≠268 435 458,

所以a2=1不成立。

当a2=9时,代入(32)式

a2(15a12- 455a10×42+3 003a8×44-6 435a6×46+5 005a4×48-1 365a2×410+105×412)

=7 700 834 727≠268 435 458，

所以a2=9不成立。

当a2=81时,代入(32)式

a2(15a12- 455a10×42+3 003a8×44-6 435a6×46+5 005a4×48-1 365a2×410+105×412)

=-1 953 389 825 937≠268 435 458，

所以a2=81不成立。

所以b=4不成立。

当b=-4时，由(27)式得

-2= 15a14-455a12×(-4)2+3 003a10×(-4)4-6 435a8×(-4)6+5 005a6×(-4)8-

1 365a4×(-4)10+105a2×(-4)12-(-4)14,

414-2= 15a14-455a12×42+3 003a10×44-6 435a8×46+5 005a6×48-

1 365a4×410+105a2×412，

268 435 454= 2×7×73×262 657=a2(15a12-455a10×42+3 003a8×44-6 435a6×46+

5 005a4×48-1 365a2×410+105×412)。

(33)

(33)式要成立,则a2=1。

代入(33)式,有

a2(15a12- 455a10×42+3 003a8×44-6 435a6×46+5 005a4×48-1 365a2×410+105×412)

=632 712 863≠268 435 454。

所以b=-4不成立。

当b=8时，由(27)式得

1= 15a14-455a12×82+3 003a10×84-6 435a8×86+5 005a6×88-

1 365a4×810+105a2×812-814，

814+1= 15a14-455a12×82+3 003a10×84-6 435a8×86+5 005a6×88-

1 365a4×810+105a2×812，

4 398 046 511 105= 5×13×29×113×1 429×14 449=a2(15a12-455a10×82+3 003a8×84-

6 435a6×86+5 005a4×88-1 365a2×810+105×812)。

(34)

(34)式要成立,则a2=1。

代入(34)式,有

a2(15a12- 455a10×82+3 003a8×84-6 435a6×86+5 005a4×88-1 365a2×810+105×812)

=5 832 182 808 143≠4 398 046 511 105。

所以b=8不成立。

当b=-8时，由(27)式得

-1= 15a14-455a12×(-8)2+3 003a10×(-8)4-6 435a8×(-8)6+5 005a6×(-8)8-

1 365a4×(-8)10+105a2×(-8)12-(-8)14，

814-1= 15a14-455a12×82+3 003a10×84-6 435a8×86+5 005a6×88-

1 365a4×810+105a2×812，

4 398 046 511 103= 32×72×43×127×337×5 419=a2(15a12-455a10×82+3 003a8×84-

6 435a6×86+5 005a4×88-1 365a2×810+105×812)。

(35)

(35) 式要成立,则a2=1,a2=9,a2=49,a2=441。

当a2=1时,代入(35) 式，有

a2(15a12-455a10×82+3 003a8×84-6 435a6×86+5 005a4×88-1 365a2×810+105×812)

=5 832 182 808 143≠4 398 046 511 103，

所以a2=1不成立。

当a2=9时,代入(35) 式，有

a2(15a12-455a10×82+3 003a8×84-6 435a6×86+5 005a4×88-1 365a2×810+105×812)

=-2 921 066 949 033≠4 398 046 511 103,

所以a2=9不成立。

当a2=49时,代入(35) 式，有

a2(15a12-455a10×82+3 003a8×84-6 435a6×86+5 005a4×88-1 365a2×810+105×812)

=70 518 915 341 567≠4 398 046 511 103,

所以a2=49不成立。

当a2=441时,代入(35) 式，有

a2(15a12-455a10×82+3 003a8×84-6 435a6×86+5 005a4×88-1 365a2×810+105×812)

=-17 258 894 904 586 459 257≠4 398 046 511 103,

所以a2=441不成立。

所以b=-8不成立。

所以当x≡1(mod 2)时,不定方程x2+64=y15,x,y∈Z无整数解。

(2)x≡0(mod 2)，易知x为偶数,y也是偶数,则令x=2x1,y=2y1,x1,y1∈Z，代入(24)式得

(2x1)2+64=(2y1)15，

即

x12+16=213y115。

易知x1为偶数,则令x1=2x2，x2∈Z，则

(2x2)2+16=213y115，

即

x22+4=211y115。

易知x2为偶数,则令x2=2x3，x3∈Z，则

(2x3)2+4=211y115，

即

x32+1=29y115。

(36)

易知x3为奇数,则令x3=2x4+1，x4∈Z代入(36)式得

(2x4+1)2+1=29y115，

即

2x42+2x4+1=28y115。

(37)

由(37)式知左边2x42+2x4+1≡1(mod 2),而右边28y115≡0(mod 2)，则产生矛盾。

所以当x≡0(mod 2)时,不定方程x2+64=y15无整数解。

综上,不定方程x2+64=y15(x,y∈Z)无整数解。

2 结论

不定方程的整数解问题是一个悠久的研究课题,许多数学家都有所研究,推动着不定方程整数解问题的发展,本文研究了x2+4n=y15(n=1,2,3)的整数解问题,得出了不定方程x2+4n=y15(n=1,2,3)无整数解的结论和证明。

[1] 柯召,孙琦.谈谈不定方程[M].哈尔滨：哈尔滨工业大学出版社,2011.

[2]LebesgueVA.SurLimpossibiliteennombreentiersdeequationxm=y2+1[J].Nouvelle Annals of Mathematics，1850,9(1):178-181.

[3] Nagell T.Sur Limpossibilite de quelques equations deux indeterminees[J].Norsk Marem Fornmings Skrefter Senel,1921,13(1):65-82.

[4] 孙树东.不定方程x2+64=y13的整数解[J].吉林师范大学学报(自然科学版),2015,(3):78-80.

[5] 杨全.关于不定方程x2+16=y9的解[J].牡丹江大学学报,2013,22(8):119-120.

[6] 李中恢,张四保.关于不定方程x2+16=y11的解[J].海南大学学报(自然科学版),2009,27(3):216-218.

[7] 张杰.关于不定方程x2+64=y7的解的讨论[J].重庆工商大学学报(自然科学版),2012,29(3):27-28.

[8] 潘承洞,潘承彪.代数数论[M].第2版.哈尔滨：哈尔滨工业大学出版社,2014.

【责任编辑 牛怀岗】

The Solution on Diophantine Equationx2+4n=y15(n=1,2,3)

SHANG Xu，WANG Ze-deng

(College of Mathematics and Information Engineering，Zhejiang Normal University，Jinhua 321000，China)

The integer solution of Diophantine equation is an important problem of the number theory，the problem of integer solution to the Diophantine equationx2+4n=y15(x,y∈Z) is discussed by using the methods of algebraic number theory and congruence theory，and the Diophantine equationx2+4n=y15(n=1,2,3)whichhasnointegersolutionisproved.

diophantine equation; integer solution; algebraic number theory

O156.2

A

1009-5128(2017)08-0033-09

2016-12-23

国家自然科学基金项目：神经网络的代数构造和可算性(11171137)

尚旭(1989—),男,陕西西安人,浙江师范大学数理与信息工程学院硕士研究生,主要从事初等数论研究；王泽灯(1991—),男,浙江义乌人,浙江师范大学数理与信息工程学院硕士研究生,主要从事数论和复函数空间上的算子理论研究。