含有伪Smarandache函数的方程的求解问题

杨 明 顺

(渭南师范学院 数理学院，陕西 渭南714099)

【自然科学基础理论研究】

含有伪Smarandache函数的方程的求解问题

杨 明 顺

(渭南师范学院 数理学院，陕西 渭南714099)

伪Smarandache函数；原根；方程；正整数解

0 引言

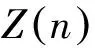
1 引理及证明

引理1[5]设n>1为正整数，a为任意整数且(a,n)=1，则aφ(n)≡1(modn)，其中：φ(n) 为Euler函数，即φ(n)表示不超过n且与n互素的正整数的个数。

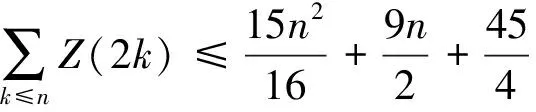
证明 以下分两种情况进行讨论:

(1)当n=2m(m为自然数)为偶数时，有

(1)

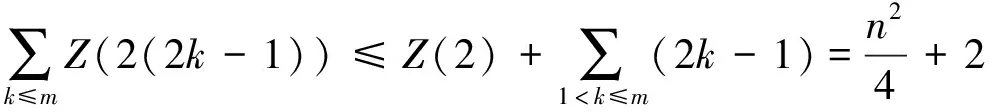
(2)

(3)

当2k-1>4时,注意到：Z(4(2k-1))≤2k-2。如果k≡1(mod 4),则Z(4(2k-1))≤2k-1;如果k≡0(mod 4)，则Z(4(2k-1))≤3(2k-1)-1;如果k≡2(mod 4)，则Z(4(2k-1))≤3(2k-1);如果k≡3(mod 4)，则有

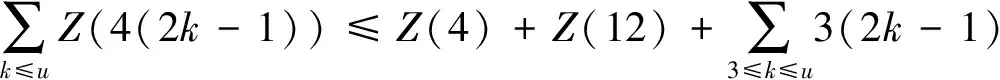
(4)

注意到Z(2n)≤4n-1 ,因此

(5)

由(3)(4)(5)式可得

(6)

由(1)(2)(6)式可得

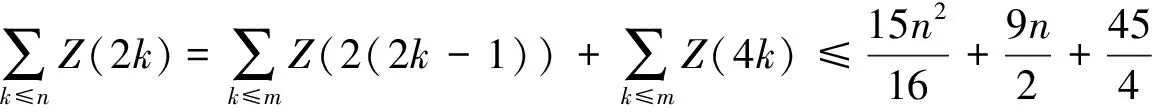
于是，证明了当n为偶数时结论成立。

(2)当n为奇数时，设n=2m+1(m为自然数),利用Z(2(2m+1))≤2m+1及上面已经证明的结果有

于是，完成了引理的证明。

引理3[7]若p为奇素数,则模p有原根。

(2)因为δs(s=1,2,…,r)是τ的因数,而1,2,…,p-1中任一数的指数在δ1,δ2,…,δr中出现,故xr≡1(modp),x=1,2,…,p-1,即xr≡1(modp)至少有p-1个解,从而p-1≤r,但由指数的性质可知δs|p-1 (s=1,2,…,r),故τ|p-1,由此可得τ≤p-1,故τ=p-1。

引理4 若p为奇素数,则模pα有原根,其中α≥1为整数。

证明 不妨设α>1。由于g是模p的原根,则(g,p)=1,因此存在整数x0,使得gp-1=1+px0,于是,对于任意的整数t有

(g+pt)p-1=gp-1+p(p-1)tgp-2+…=1+p(x0-gp-2t)+p2Q2。

其中：Q2∈Z。

从而(g+pt)p-1≡1+p(x0-gp-2t)(modp2),当p不能整除x0时,取t0=0；当p能整除x0时,取t0=1,故p不能整除x0-gp-2t0=y0,于是

(g+pt0)p-1=1+py0≡1(modp2)，

(g+pt0)p(p-1)=(1+py0)p=1+p2y1。

因此，当p不能整除y1时,同理可得

(g+pt0)p2(p-1)=(1+p2y1)p=1+p3y2,

(g+pt0)p3(p-1)=(1+p3y1)p=1+p4y3，

……

(g+pt0)pα-1(p-1)=(1+pα-1y1)p=1+pαyα-1。

其中：yα-1≡yα-2≡…≡y0(modp),因此，p不能整除yi(0≤i≤α-1)。

设g+pt0对模pα的指数为δ,则(g+pt0)δ≡1(modpα),由此即得(g+pt0)δ≡1(modp),但g+pt0是模p的一个原根,故p-1能整除δ。另一方面,由δ的定义知δ|φ(pα),即δ|pα-1(p-1),故δ=pr-1(p-1),1≤r≤α,由此结果可得1+pryr-1≡1(modpα),即pryr-1≡1(modpα),从而有r≥α,故r=α,g+pt0是模pα的一个原根。

引理5 关于模m(>1)有原根的充要条件是m是形如2,4,pk,2pk的数，其中:p为奇素数，k为正整数。

证明 (1)必要性：

若m不具备定理中的形式，则

m=2k(k≥3)，

(7)

(8)

(9)

其中：pi(1≤i≤l)为奇素数，ki(1≤i≤l)为正整数。

若m是形如(8)式的数，那么对任意a，(a,m)=1，有

aφ(2k)≡1(mod 2k)，

aλ(m)≡1(mod 2k)，

aλ(m)≡1(modpiki),1≤i≤l，

aλ(m)≡1(modm)。

(10)

(2)充分性：

1)若m=2n。当n=1时，m=2，此时φ(m)=1，显然1是它的原根。当n=2时，m=4，此时φ(m)=2，易知1，3是模4的简化剩余系，显然3是它的原根。当n≥3时，对任意奇数a，由于a=2a1+1，从而a2=4a1(a1+1)+1≡1(mod 23)， 则

3)若m=2pk，此时φ(m)=φ(2)φ(pk)，g是模pk的原根，那么，当g为奇数时，g是模m的原根，这是因为(g,m)=1，gφ(m)≡1(modm)，假设g关于模m的阶数λ<φ(m)，则从gλ≡1(modm)，即有gλ≡1(modpk)，而这与g是模pk的原根的假设矛盾，因此λ=φ(m)，于是g是模m的原根。当g为偶数时，因为g+pk是pk的原根，而g+pk为奇数，所以g+pk也是模m的原根。

于是完成了引理的证明。

2 结论及证明

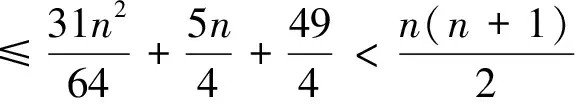
定理2 设n是存在原根的正整数，则伪Smarandache函数Z(n)为n的原根当且仅当n=2,3,4。

证明 显然，Z(2)=3是2的一个原根，Z(4)=7是4的一个原根，现在考虑n=pα，其中：p为奇素数。若Z(n)是模n=pα的原根。则由Z(n)的定义及性质知Z(n)=pα-1，所以pα-1为模n=pα的原根。又由于Z2(n)=(pa-1)2≡1(modpa)且pα-1为模n=pα的原根，所以 2=φ(pα)=pa-1(p-1),由此式立刻推出α=1，p-1=2。即就是p=2+1=3。因此，当n=pα(p为奇素数)时，Z(n)为n的原根当且仅当n=p=3。

当n=2pα时，注意到前面列出Z(n)的性质，我们分两种情况讨论：

(1)若pα≡3(mod 4)，则由Z(n)的定义及性质可得Z(n)=pα，因为(pα,2pα)=pα>1，所以Z(n)=pα不可能为n=2pα的原根。

(2)若pα≡1(mod 4)，则由Z(n)的定义及性质可得Z(n)=pα-1。因为(pα-1,2pα)=2>1，所以Z(n)=pα-1也不可能为n=2pα的原根。

综合以上结果及引理4、引理5可得，Z(n)为n的原根当且仅当n=2,3,4。

[1]SmaradacheF.OnlyProblems，NotSolutions[M].Chicago:XiquanPublishingHouse，2001.

[2]GorskiD.Thepseudo-Smarandachefunction[J].SmarandacheNotionsJournal,2002，13：140-145.

[3]LIUYah-hi.OntheSmarandachePseudoNumberSequenc[J].ChineseQuarterlyJournalofMathematics，2006，21(4)：581-584.

[4]WANGJinrui.OntheSmarandachefunctionandtheFermatnumber[J].ScienfiaMagna，2008，4(2):25-28.

[5] 张文鹏.初等数论[M].西安:陕西师范大学出版社,2008.

[6] 张爱玲.关于伪Smarandache函数的一个方程及其正整数解[J].西北大学学报(自然科学版)，2008，38(4):535-538.

[7] 闵嗣鹤，严士健.初等数论[M].北京:高等教育出版社,2003.

[8] 朱敏慧.关于Smarandache函数与费尔马数[J].西北大学学报(自然科学版)，2010，40(4):583-585.

【责任编辑 牛怀岗】

The Solution of Equations Involving Pseudo Smarandache Functions

YANG Ming-shun

(School of Mathematics and Physics，Weinan Normal University，Weinan 714099，China)

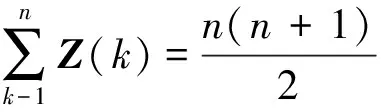
pseudo function; primitive root; equation; positive integer solution

O

A

1009-5128(2017)08-0005-05

2016-12-17

陕西省自然科学基金资助项目：Mocktheta函数理论及其交叉应用研究(2016JM1004)；陕西省教育厅自然科学研究计划项目：Hurwritz-zeta函数高阶导函数的新型均值计算及应用研究(16JK1265)；渭南师范学院科研计划项目：数论函数及其在大数据处理方面的应用研究(15YKF005)；渭南师范学院教育科学研究项目：协同创新下师范生职业技能的培养(2015JYKX016)

杨明顺(1964—)，男，陕西渭南人，渭南师范学院数理学院教授，主要从事数论研究。