“异分母分数加、减法”教学设计

王宝英

教学内容：人教版数学五年级下册第93～94页。

教学过程：

一、复习旧知，激活经验

1.口算。1/5+3/5= 6/7-3/7

指名回答后追问：你是怎么算的？为什么这样算？

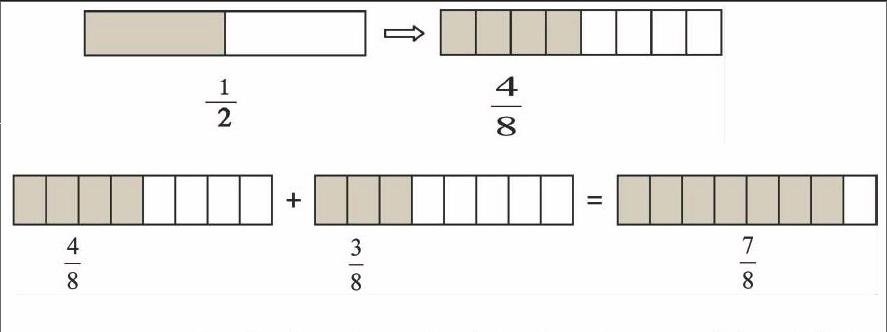
2.涂色表示“1/4+2/4”的计算过程。

让学生在练习卡上涂色后指名展示和说理。

教师引导学生看图、质疑：为什么1/4的这一块能和2/4的这两块合起来？（1/4和2/4的单位都是相同的一个扇形，单位相同就能相加。）

3.计算同分母分数的加、减法，为什么可以分母不变，只把分子相加、减？（分母不变就是分数单位相同）

设计意图：这里抓住新旧知识的连接点，分层复习同分母分数加、减法的计算知识，激活原有经验，调动迁移能力。先通过口算说理，激活同分母分数加减法的算理与算法；再借助图示，操作说理，调动数学活动的经验；最后以“计算同分母分数的加、减法，为什么可以分母不变，只把分子相加减？”的问题，提升学生的思维，为探索异分母分数加、减法的算理与算法做好充分的准备。

二、探索交流，理解算理，构建算法

课件出示：用一块布的1/2做电视套，3/8做桌布，一共用了这块布的几分之几？

1.观察思考，引出课题。

先让学生阅读题目，观察图片。

（1）要解决“一共用了这块布的几分之几”怎样列式？

（师生交流后板书：1/2+3/8=）

（2）这个算式与前面学过的分数加法有什么不同？能直接相加吗？为什么？（分数单位不同不能直接相加）

师生交流后引出课题：异分母分数的加法。（板书）

2.借助直观，揭示“分母不同不能直接相加”的事实。

引导学生观察图片：从图中看，1/2和3/8的单位一样大吗？谁来指一指1/2的单位是哪块长方形？3/8的单位是哪块长方形？这两块长方形一样大吗？不一样大，说明什么？能直接相加吗？

交流后明确：图中1/2和3/8相加，就是1个大长方形和3个小长方形相加，长方形的大小不一样就是分数单位不一样，所以不能直接相加。

3.动手操作，尝试计算。

分数单位不同不能直接相加，那该怎么办呢？你能用已经学过的知识来解决吗？请同学们认真思考，然后把你的想法写出来，找不到方法的，可以用课前准备好的长方形白纸折一折、涂一涂、拼一拼。

预设1：先通分再计算。

1/2=4/8 4/8+3/8=7/8

预设2：用折纸的方法，把1/2的这张纸再平均分成8份，使{变成詈，再把4个1/8和3個1/8拼起来，就得到7个1/8。

4.展示交流，理解算理，明确算法。

（1）交流辨析，感悟算理。

谁来向大家展示和交流你的想法？（让学生上台板演或操作）

针对方法1追问：通分的目的是什么？不通分行吗？

针对方法2质疑：为什么要把1/2的这张纸也平均分成8份？分成8份后，原来的1/2变成了几分之几？为什么现在就可以相加了？

（2）观察比较，明确算法。

同学们仔细观察，这两种方法有什么相同点和不同点？

同桌交流后指名汇报，教师利用课件再次演示转化过程，引导学生沟通两种方法的联系。

通过比较，使学生发现两种方法都是用通分把异分母分数转化成同分母分数，只是表达方式不同。

归纳概括：通过研究，可以怎样计算异分母分数的加法？（用通分把异分母分数转化成同分母分数，再按同分母分数的加法计算方法进行计算。）

5.迁移类推，探索异分母分数的减法计算方法。

课件：5/6-1/3=

学会了异分母分数的加法计算，会计算异分母分数的减法吗？怎样计算？试一试。

（1）学生独立计算；

（2）指名板演，交流算理和算法。

质疑：异分母分数的加法和减法，都是用什么方法把异分母分数转化成同分母分数？

交流后教师小结：异分母分数的减法与加法相同，都是先通分把异分母分数转化成同分母分数，再按同分母分数的计算方法进行计算。

（教师相机完善板书：减法）

设计意图：为了帮助学生理解“异分母分数为什么不能直接相加”这一算理，教学特意选取便于学生操作的生活问题，让学生在解决问题的过程中，充分感知“单位不同不能直接相加”的事实，进而掌握用通分把异分母分数转化成同分母分数的方法。

首先，通过1/2和3/8的图示，发现1/2的单位是一块大长方形，3/8的单位是一块小长方形，所以1块大长方形和3块小长方形就不能相加，进而明确1/2和3/8的分数单位不同不能直接相加。接着，让学生带着“如何把异分母分数转化成同分母分数”的问题，探索“1/2+3/8”的计算方法。利用复习环节中激活的经验，学生一定能想到通分的方法，因此，教学预设了直接通分和操作通分的方法。针对两种通分的方法，教师抓住关键性问题进行追问和质疑，使学生在辨析中明白不管是直接通分还是操作通分，都是把异分母分数转化为同分母分数，再按同分母分数的计算方法进行计算。学会了异分母分数的加法计算，借助知识迁移的规律，便能水到渠成地类推出异分母分数的减法计算方法。

三、学以致用，巩固算法

1.把异分母分数的算式转化成同分母分数的算式。

指名交流，说明：怎样把异分母分数转化成同分母分数？

2.不计算。观察下面的计算对吗？为什么？

7/10-3/5=4/5 （ ） 1/2+2/7=9/14（ ）

独立判断后指名交流，说明：错在哪里？应该怎样计算？

设计意图：有效的练习是学生巩固新知、形成技能的必要手段。因此，练习围绕教学重难点分层设计，第1题以填空的形式，让学生把异分母分数的算式转化成同分母分数的算式，专门检查通分的方法；第2题，通过错例辨析，进一步加深异分母分数加减法算理的理解。

四、总结反思，提炼算法

这节课学习了什么计算？异分母分数的加、减法与同分母分数的加、减法有什么不同？计算时应该注意什么？

通过交流，教师相机板书：

转化

异分母分数→同分母分数

设计意图：引导学生回顾、梳理知识，不仅沟通新旧知识的内在联系，而且进一步完善学生的认知结构，发展数学思考的能力。