把心中的数学画出来
陈昱


什么是“数学画”?简而言之,即儿童运用直观之“形”表征抽象之“数”,从而帮助理解数学概念、解决数学问题,其立足点是儿童认知特点和数学学科本质。所以说,“数学画”教学既有儿童趣味,又深蕴数学真味,是引导儿童认知逐渐“数学化”的过程。
一、“数学画”的形态
1.画数学,促进概念理解。
(1)画“数”。在第一学期起步阶段,教师只是要求孩子“画出心目中的数学”,比如:学习了自然数的认识,孩子回家画出自己心目中的“数”。从孩子们的画作看,只有个别孩子表现的是“数像什么”(如图1),或者将数字拟人化(如图2),大多数孩子都画出了“数是什么”(如图3),少数用同一幅画既表示出“数像什么”又表示出“数是什么”(如图4)。有一个孩子一口气画出6种不同场景表示“0”,既有“1个也没有”、也有“起点”的含义,生动活泼,极富想象力和童趣(如图5)。
(2)画“生活中的数学”。国庆节假期孩子们观察生活,画出“生活中的数学”,很有意思,每幅画都是儿童视角下的多彩数学(如图6、图7)。
(3)画加减法。后来,孩子们逐渐学会用简单的数学符号表达数学含义,画加减法的算式意义。在不断进步的同时,他们渐渐形成了自己的“数学画”风格,这可以从画连加、连减的画作对比中清楚分辨(如图8、图9)。
2.画思路,辅助问题解决。到了一年级下学期,孩子们已经会用“数学画”辅助解决一些思考题,也就是画出问题的思路。我们深刻感受到,“数学画”不仅因其形象直观、富有童趣而被孩子们广泛喜爱和接受,更重要的是通过数形结合,特别是几何直观,将比较复杂、困难的问题变得简单、容易,能够培养学生有序思考、大胆猜想、勇于尝试、逐步抽象等能力,成为学生学习数学的思维拐杖。
(1)送给小明多少支彩笔?
(2)这幢楼一共有几层?
二、“数学画”的特点
1.“数学画”回归儿童视角。
心理学研究表明,7~8岁是儿童概念性工具发展的一个决定性转折点,这个阶段儿童的运演已经不再受自我中心和中心化的影响,逐渐具有可逆性、守恒性以及依賴于实物的整体性,处于这一阶段的儿童很难回答“a比b长,b比c长,谁最长?谁最短?”的问题,但借助实物就可以回答。我们在实践中发现,图画可以达到实物同样的效果。“数学画”教学契合了低年级儿童认知规律,让我们的数学教学回归儿童视角,更有利于儿童的数学学习。
发现儿童是教育的前提,是教育成功的密码,也是教师的最高境界,“课程的方式应该是儿童的生活方式。小学数学教学应该回归儿童视角,鼓励儿童用自己喜欢的方式学习数学。儿童是天生的画家,几乎每个孩子都喜欢涂鸦,当他们用动物、植物、人物、景物乃至简单的图形、符号等这些自己熟悉的形象表达自己所理解的数学知识时,他们的心情是愉悦的,思想是自由的。
孩子们创作的一幅幅数学画满蕴浓浓的儿童趣味:在儿童眼中,数学不是灰色的、枯燥的,而是彩色的、有趣的;数学不是冰冷的、生硬的,而是温暖的、丰润的。小学数学教学只有回归儿童视角才能走向高效。
2.“数学画”尊重个性差异。
我们认识并充分尊重儿童在数学学习上的差异性,允许他们在各自的学习基础上、从已有经验出发、采用自己擅长的方法学习数学、表现数学、解决问题,尤其强调独立思考,并在自我反思和同伴交流中不断进步。下面以“豆豆在哪儿”为例具体说明:
(1)尊重学生思维的层次性差异。针对配套练习册问题:27个小朋友排成一排,豆豆排在正中间的位置,从左往右数,豆豆排第( );从右往左数,豆豆排第( )。每位学生都能通过“数学画”解决问题,作品呈现出多种思维层次,大体可分成两大类:(1)将27个人(也有用毛毛虫、苹果等代替)一个一个全部画出来的;(2)只画出部分人的。
第1类也分为不同的层次:①仅仅画出27个并指出豆豆位置的;②标有相关数字和箭头等符号表明思路的;③图文并茂,专门用文字和算式说明思路的。
第2类蕴含的数学思考更加丰富和有价值,反映的数学思维更有品质。表面上看,好像不如第1类完整美观,但只要问问小作者是怎么想的,立马令人惊喜!
生1:我画了7个后不够画了,我不想重画,就想啊想,还剩20人,心里知道每边站10人,所以豆豆在从左往右第14个,从右往左也是第14个。(如图14)
生2:因为27太多了,画不下。我想,27里有20和7,20是双数,很好分;7是单数,不好分;只要把7分好就行了!(如图15)
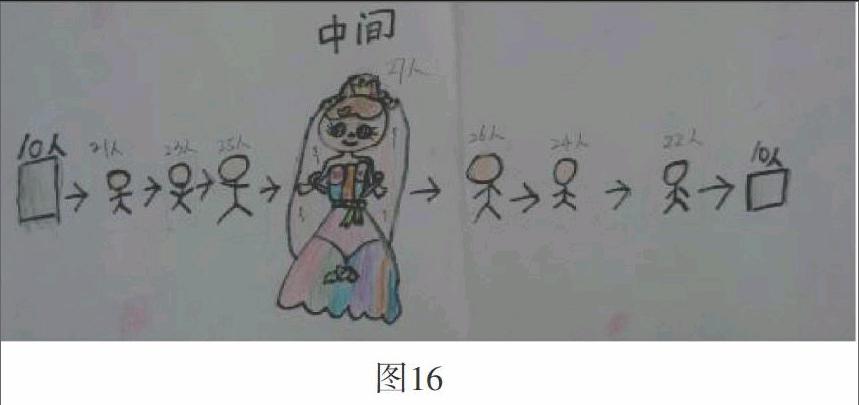
生3:27人太多了,画不下,我就画个长方形表示10人,两边就是20人,剩下的一边一个分21、22、23、24、25、26,正好分完,最后第27个不能分,放在中间,就是豆豆。(如图16)
(2)尊重学生思维的形象性差异。低年级儿童在用“数学画”解决问题过程中,启动其形象思维,会根据自己的生活经验和喜好赋予数学抽象以个性化的直观形象,让儿童的数学思考附着在具体物象上,帮助儿童理顺问题的内在关系,解决问题。所以同样的问题,甚至同样的思维层次,展现的形象却各不相同。有人物、苹果、篮球、毛毛虫等,也有简化小人、几何图形等,形象各异。
3.“数学画”鼓励想象和创新。
创新意识的培养是现代数学教育的基本任务,应体现在数学教与学的过程中。古希腊哲学家亚里士多德认为:想象力是发明、发现及其他创造活动的源泉;中国学者吴克杨说:想象力不是生来就有的先天素质,而是后天开拓的结果,它是完全能够培养的一种能力。“数学画”教学有利于培养学生的想象力和创新意识。
(1)先想后画——留给儿童自由想象的空间。“数学画”落笔之前需要思考,所以一直多以家庭作业方式出现,而且不设限制,鼓励孩子“想怎么画就怎么画”,只需围绕主题(某个数学知识或数学问题)即可,留给孩子充分的思考时间和想象空间。思考的自由避免了思维的束缚,激发了想象的力量,为孩子们的创造打开大门。
(2)边想边画——引导儿童借助图画辅助思考。对儿童而言,“数”是抽象的、难以理解和把握的;“形”是直观的、容易理解和探索的。数形结合的画图策略既可以帮助儿童理解数学概念,又可以辅助儿童分析数量关系、解决数学问题。
在画图分析的过程中,几何直观发挥巨大作用,形象直观的“形”能有效促使儿童思考和发现,找到创造性思维的生发点,给予他们无穷的启示。儿童就在这样边想边画、边画边想中体会数学的本质、寻得问题的解决方法。
(3)画过再想——教会儿童提升数学思维。
教学实践表明,对某一知识和问题的反思整理有助于儿童从整体上把握分析问题、解决问题的方法,从而有机会超越方法产生策略,感悟数学思想,提升创造能力;而欣赏和评价同伴作品则能给予儿童很好的启发,促使其优化思考。“数学画”展评便具有这样的作用:①在推介画作中整理思路、完整表达,使思路和理解更清晰更深入。②在欣赏评价他人画作中反思借鉴,使思考更全面更优化。③在改进画作中体会进步,使思考更积极更愉悦。
“数学画”沟通抽象与具象,打通已知与未知,连接生活与数学,鼓励和培养儿童的创造性思维,儿童在“数学画”教学过程中不断增进多种能力,最终使创新成为可能。
“数学画”中绚丽的色彩、变化的形象都是儿童丰富想象力的表现,教师并没有因其“失真”或不够数学化而加以批评,代之以尊重基础上的引导,增进数学思维的同时尽可能满足儿童的心理需求。
三、“数学画”的课堂展评
作为数学实践作业,“数学画”的课堂展评很重要。以第一种形态的“数学画”为例,“画数学”只是手段和方式,目的是促使学生深刻理解数学知识、准确掌握数学概念。这样的教学目标除了有赖于学生课堂上对数学知识的学习,有赖于课后在理解数学知识基础上的再创造,还要靠“数学画”展评课来引导和落实。
“数学画”展评课的大体流程是:(1)教师选择典型“数学画”课堂分层交流;(2)小作者推介画作;(3)学生提问和评议,教师点拨和引导,小作者回答和改进。具体来说,“数学画”展评课要做好三件事:
1.分享“我画的是什么,为什么这么画?”
在“数学画”的课堂展示中,首先请作者说说“我画的是什么,为什么这么画”,从而了解作者对于所画数学知识的理解情况,教师可以有针对性地加以提问和引导,力求突破学生的认识困难,扫清学习障碍,深化概念理解。
有些画作,只有听了作者的解说,我们才能看懂。比如图17,这是一位小男孩的作品,画的是他和爸爸在洗澡,老师问:“画得不错,可是这里有数学吗?”男孩立即高声答道:“有数学呀!老师,你知不知道我爸爸是怎么洗澡的?”老师捂嘴笑:“那我哪知道啊!”小男孩也得意地笑:“我爸爸可牛了!每次洗澡都带我做‘洗澡操——1、2、3、4,2、2、3、4……”边说边比画着搓澡动作……不用我多说了,孩子们眼中的数学是多么鲜活、多么有趣啊!
有的画作包含着小作者没有意识到的数学含义,需要老师点拨。如图18,小作者只提及楼房按照从高到矮可以排出第1~第5,老师可以顺势追问:“你是从高到矮排的,还可以怎么排?”“除了按高矮排,还可以按什么排?”启发学生灵活思考:还可以从矮到高排序,也可以按照从左到右或从右到左的位置顺序排序等。
有的畫作容易引起学生对数学知识的误解,需要老师“反例正用”。如图19,小作者解说中序数第1~第5(花瓶从左往右顺序)正好对应着基数1~5(花瓶中花儿的朵数),容易造成思维定式,老师可以作如下处理:
(1)追问:那从右往左数,第1~5分别在哪?
(2)拿掉其中第4个花瓶里的1朵花,问:从左往右数它还在第4个吗?为什么?
(3)打乱花瓶的位置,比如将一开始第2瓶花移到最后,问:现在它排第几?
(4)小组讨论:刚才按位置排序,插2朵花的花瓶有可能在第2,有可能不在第2;如果要使插2朵花的花瓶不论怎么数都是第2个,应该按什么排?(按花的数量从少到多排)
2欣赏“他画的是什么,可不可以这么画?”
同样的数学知识,不同学生理解不同、表达也不同。相互交流作品,多元表征,利于学生全面认识数学概念。
数字“0”,甲同学:1杯果汁喝完,是0杯;乙同学:2只小鸟从树上飞走,是0只;丙同学:5个苹果全部落下,树上是0个苹果……让学生思考:“他画的是什么?可不可以这么画?”让学生认识:原来0还可以这样画!
学生间互动分享,可以相互补充、相互启发。如在展评课上,为了引导孩子们增进概念理解和数学思考,我和孩子们展开互动:
师(问图20的小作者):你的画里有第1~5吗?在哪呢?看不懂哦!
还没等他回答,同桌站起来了:我知道!房顶有5层,我来指给你们看!(自告奋勇地上台,从上向下一路指)第1、第2、第3、第4、第5。
小作者笑了:可是我画的是从底下往上面第1~5层。(台上的立马尴尬)
师:那他指错了?这样数出第1~5行吗?(短暂的沉默)
小作者:也行!从下往上数和从上往下数出来的不一样。
师:你上来指一指、数一数吧!
同桌:我俩有一个是一样的!(众人迷惑)
师:哪一个你俩一样?
同桌:第3层的中间这里。(掌声)
3.反思“还可以怎么画,它到底表示什么意思?”
还以0为例,追问:“0还可以怎么画?这样画下去能画多少?”“为什么不同的图画表示的都是0?它们有什么共同点?”引导学生在之前学习基础上进一步观察、比较、反思、概括,得出:0表示1个也没有(还表示起点)。从而从具体情境中抽象出数0。如此,学生头脑中才真正建立起0的概念,而不是停留在“0像鸭蛋圆又圆”的“认0”和“写0”层面。像这样借助形象直观的图画辅助学生进行概括,符合儿童心理学相关理论。
台湾名师吴如皓说:“曾经有人问一个科学家,如何保持热情?科学家回答:一是数学,二是数学,三还是数学。而我曾问学生最痛恨的学科是什么?学生回答:一是数学,二是数学,三还是数学。”同样是数学,为什么给科学家与学生的感受有如此大的反差?央视主持人崔永元曾说:“数学是噩梦。”网上调查,竟有超七成网友支持数学退出高考……这些现象难道还不能促使我们好好反思我们的数学教学吗?就小学数学教学而言,基于儿童的心理特征和认知规律,既有儿童趣味又有数学味的教学才是受学生欢迎的,才是可持续的。“数学画”教学正是基于以上考虑的新尝试。
责任编辑:徐新亮

