基于改进多尺度熵与VPMCD的滚动轴承故障诊断

姜战伟，郑近德，潘海洋，潘紫微

(安徽工业大学 机械工程学院，安徽 马鞍山 243032)

基于改进多尺度熵与VPMCD的滚动轴承故障诊断

姜战伟，郑近德，潘海洋，潘紫微

(安徽工业大学 机械工程学院，安徽 马鞍山 243032)

多尺度熵(Multiscale entropy,MSE)是一种衡量时间序列复杂性的方法，针对其粗粒化过程由时间序列长度变短而导致熵值不精确、波动较大等问题，提出一种改进的多尺度熵(Improved multiscale entropy,IMSE)算法。在此基础上，结合迭代拉普拉斯得分(Iteration Laplacian Score,ILS)特征选择和多变量预测模型(Variable predictive model based class discriminate,VPMCD)，提出一种新的滚动轴承智能故障诊断方法。最后，将提出的方法应用于滚动轴承试验数据分析，并与现有方法进行对比。结果表明，提出的方法不仅能够有效地识别滚动状态和故障类型，而且其诊断效果优于现有方法。

振动与波；多尺度熵；特征降维；多变量预测模型；滚动轴承；故障诊断

在滚动轴承的运行过程中，载荷和转速波动等外部因素和内部故障往往使轴承振动信号产生非线性和非平稳特征。从故障振动信号中提取故障状态信息对于滚动轴承故障诊断而言至关重要。非线性分析方法由于能够有效地提取潜在的其他线性方法无法提取的故障特征信息已经成功应用于机械故障诊断中。司景萍等将信息熵与小波变换相结合，提取发动机故障特征[1]；曾求洪等将小波包和近似熵应用于异步电机故障诊断[2]；郑近德等将排列熵与LCD结合，有效提取出滚动轴承故障特征信息[3]；邹龙庆等将样本熵成功应用于往复压缩机故障诊断[4]。郑近德等将多尺度熵应用于滚动轴承故障诊断中，有效地实现滚动轴承故障类型的诊断[5]；陈慧等将MSE与PNN结合应用于滚动轴承故障诊断中[6]。但是，MSE粗粒化序列的计算中，粗粒化过程会随着尺度的增加而缩短时间序列的长度，这可能会产生不精确的熵估计或当时间序列太短时引起未定义熵，熵值的偏差也会随着粗粒化序列长度减小而增大。为了克服MSE方法的不足，本文提出了改进的多尺度熵(IMSE)算法，其粗粒化采用滑动平均化过程克服了传统MSE方法由于尺度因子的增大导致时间序列的迅速变短而引起不精确的熵估计，一致性和稳定性更好。

同时为了避免提取的特征向量维数过高，导致许多有效信息淹没在高维数据中。将迭代拉普拉斯得分（iteration Laplacian score，ILS）[7]应用于故障特征降维。ILS通过其局部保持能力，在每次迭代中剔除最不相关特征来逐渐更新近邻图，选择的特征子集比传统拉普拉斯得分(Laplacian Score,LS)[8-11]更能体现数据潜在的流行结构，是一种有效的特征降维算法。同时为了实现故障类别的自动识别，需要选择合适的故障分类器。最近，Raghuraj等提出的基于多变量预测模型的模式识别(Variable predictive model based class discriminate,VPMCD)方法充分利用特征值之间的内在变量关系，针对不同的系统或类别，建立能够反映状态特征值之间关系的预测模型，再利用预测模型对被测试样本特征值进行预测，以预测误差平方和作为判别分类的依据，进一步进行模式识别[12]。

基于上述分析，将提出的改进多尺度熵与ILS和VPMCD相结合，提出了一种新的滚动轴承故障诊断方法。将提出的方法应用于滚动轴承试验数据分析，结果表明了论文方法的有效性。

1 改进的多尺度熵

1.1 多尺度熵

Costa等提出的多尺度熵算法，通过多尺度来量化时间序列的复杂性。MSE方法主要步骤如下：

(1)给定原始时间序列{Xi}={x1,x2,…,xN}，为了得到粗粒化时间序列，原始时间序列被分割成尺度因子τ的无重叠窗，根据式(1)构造粗粒时间序列如下

式中τ是尺度因子，每个粗粒化序列的长度是原时间序列长度的当尺度因子为1时，粗粒时间序列与原始序列相同。

(2)计算每个粗粒化时间序列的样本熵，并将所有熵值看成尺度因子的函数。

从粗粒化过程可以看出，随着尺度因子的增加，时间序列的长度会急剧减小，这导致不同粗粒时间序列的样本熵估计误差增大和不精确的熵估计。

1.2 改进的多尺度熵

从信号处理的角度来看，MSE算法中的粗粒化过程有两部分组成，一是在长度为τ的窗口内平均数据来降低高频成分，二是在尺度因子τ下，粗粒化后的数据被降低了采样率。实质上降低采样率减少粗粒时间序列的长度，在大的尺度上可能会导致不精确甚至未定义的熵估计。

为了克服这一缺陷，提出改进的MSE，IMSE方法分为两个过程：

(1)对于给定原始时间序列{Xi}={x1，x2，…，xN}，执行滑动平均化过程以得到不同时间尺度，构造滑动平均化时间序列，根据(2)式

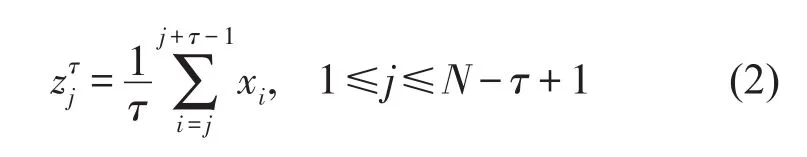
式中zτ表示在尺度因子τ下的滑动平均化时间序列。

(2)以τ作为样本熵中的时间延迟因子，计算在每个尺度因子τ下的滑动平均化时间序列的样本熵。由此定义改进的多尺度熵如下

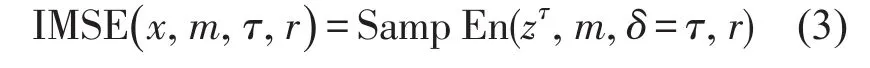
式中δ为时间延迟。

在原MSE方法中，对于所有粗粒尺度，粗粒时间序列的样本熵的计算采用统一的时延(δ=1)。粗粒序列的长度在尺度因子为τ时，减小到N τ，所以在尺度因子τ下，用以计算样本熵的样板向量的数目为此时，匹配样板向量的总数目为Nc,τ=((Nτ-1)×Nτ)/2，而提出的滑动平均化时间序列在尺度为τ时的长度为所以在IMSE方法中，以延时τ计算的样本熵的样板向量的数目为匹配样板向量的总数目为

根据上述分析可知，在IMSE中的样板向量数目比MSE方法中多，在样本熵的计算中更多数目样板向量的使用能够避免获得未定义的熵值以及会获取更精确的熵估计。

1.3 IMSE与MSE仿真对比分析

为了将IMSE与MSE进行对比，分别对不同长度的高斯白噪声信号和1/f噪声信号进行分析，两者的时域波形如图1所示。

分别采用MSE和IMSE对长度N=2 048，4 096，6 192，8 192和10 240的白噪声与1/f噪声进行分析，结果如图2所示，其中m=2，r=0.15 SD。由图2可以看出，首先，随着尺度因子的增加，白噪声的MSE和IMSE曲线逐渐减小，1/f噪声的MSE和IMSE趋于常数，但是白噪声和1/f噪声的MSE曲线随着尺度因子增大，特别地在较大尺度上熵值波动范围比较大，而IMSE曲线随着尺度因子的增大变化较平缓。这说明随着尺度因子的增加IMSE比MSE得到稳定熵值的一致性更好；其次，当数据长度N大于2 048时，不同长度数据的MSE或IMSE曲线相差很小，这说明数据长度对MSE和IMSE的计算影响较小；再者，白噪声IMSE（或MSE）曲线随着尺度因子增大而减小，这说明白噪声信号只在尺度较小的粗粒序列中包含重要的特征信息；而1/f噪声的IMSE（或MSE）随着尺度因子的较大变化较小，几乎趋于平稳，且在大部分尺度上1/f噪声的熵值大于白噪声的熵值。这说明1/f噪声包含丰富的特征信息，要比白噪声信号具有更复杂的结构特性。

为了研究MSE和IMSE的统计稳定性效果，对白噪声和1/f噪声进行MSE和IMSE分析，其中随机产生200组独立噪声数据，每组数据包含1 000数据点，仿真结果如图3所示。对于如图3(a)所示白噪声，利用MSE和IMSE计算的熵的均值几乎相等，但是IMSE的标准差比MSE的标准差小很多，这说明MSE和IMSE方法几乎有相当的统计稳定性，然而IMSE方法比MSE方法提供更精确的熵估计。对于如图3(b)所示1/f噪声，当粗粒尺大于11时，MSE方法引起未定义熵，而IMSE方法对所有粗粒尺度都能计算得到熵值。通过对比传统MSE方法可以看出，提出的IMSE方法更能有效提取白噪声和1/f噪声的不同结构特性以及提供更精确的熵值估计。

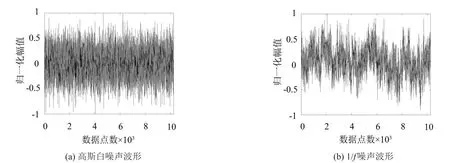
图1 高斯白噪声与1/f噪声的波形

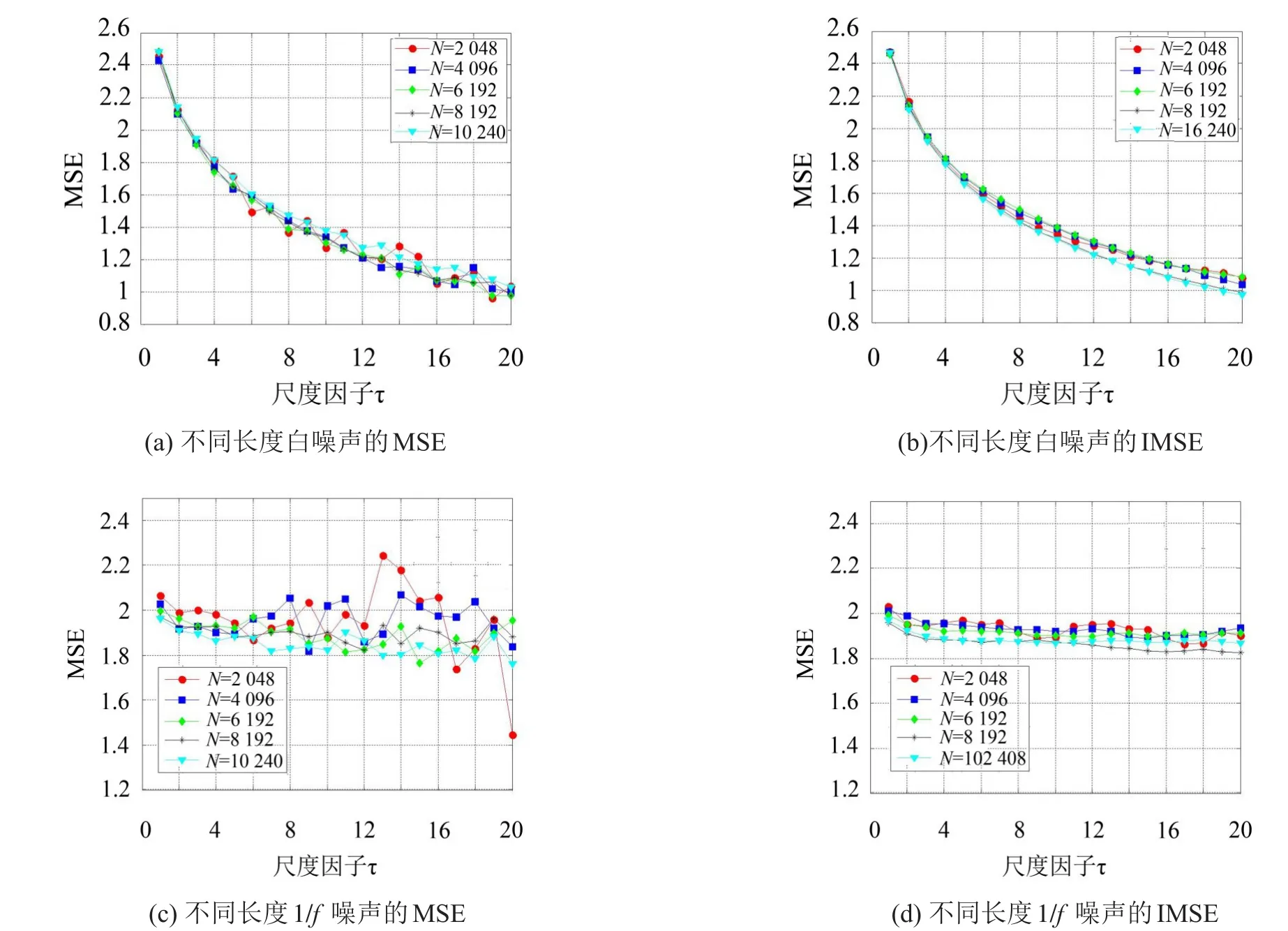
图2 不同长度的高斯白噪声和1/f噪声的MSE和IMSE曲线

2 基于IMSE、ILS和VPMCD的滚动轴承故障诊断方法

2.1 方法步骤

论文提出的基于IMSE、ILS和VPMCD的滚动轴承故障诊断方法步骤如下：

(1)假设滚动轴承的运行状态包含K种类型，每种状态采集N组样本；

(2)提取每类原始振动信号的IMSE，每组样本得到r个特征值，组成特征向量矩阵：RN×τmax，τmax是IMSE算法中最大尺度因子，一般小于等于20；

(3)每种状态各取1/2N组作为原始训练样本，其余作为原始测试样本。采用ILS对原始训练样本特征值依照重要性进行排序，将得分较高的前p个序列对应的特征值组成敏感状态低维特征向量矩阵，从而实现了降维，得到一个反映振动信号内在信息的低维训练样本集，通过VPMCD训练，建立预测模型其中k=1、2、…、g代表不同类别，i=1、2、…、p代表不同的特征值。一般地，p取5；

(4)依据原始训练样本特征值的ILS排序，原始测试样本同样取ILS序列中得分较高的前p个序列对应的原始测试样本特征值作为低维测试样本集。用训练好的数学预测模型对测试样本进行分类，根据VPMCD分类器的输出结果来确定滚动轴承的工作状态和故障类型。

2.2 实验验证

为了验证提出方法的有效性，将其应用于试验数据分析。试验数据采用美国Case Western Reserve University的滚动轴承试验数据[13]。测试轴承为6205-2RSJEM SKF深沟球轴承，使用电火花加工技术在轴承上布置单点故障。考虑转速1 730 r/min、负载3HP条件下正常以及转速1 730 r/min、负载3 HP条件下，故障直径大小与深度分别为0.177 8 mm和0.279 4 mm的外圈、内圈和滚动体故障的滚动轴承振动信号。采样频率为12 kHz，采集到具有局部单点点蚀的内圈（Inner Race,IR）、外圈（Outer Race,OR）、滚动体故障（Ball Element,BE）和正常（Norm）四种状态的振动信号，每种状态取29组数据，每组数据长度为4 096。

将提出的方法应用于实验数据分析，步骤如下：

(1)提取每类原始振动信号的IMSE，每种状态取29组样本，每组样本得到20个特征值，四种状态共得到116组样本，组成特征向量矩阵：R116×20，τmax取20；四类状态的时域波形如图4所示。

由于背景环境的影响，从时域波形上很难区别四种状态。四类状态的IMSE曲线如图5所示。

从图5中可以看出，在大部分尺度上，正常轴承的振动信号熵值较大，且随着尺度因子的增大变化平缓；而三种具有故障的滚动轴承的振动信号的IMSE曲线出现明显的逐渐递减趋势。这是因为当轴承在正常工作情况下，振动虽然是随机振动，但这种随机性不同于白噪声而类似于1/f噪声，其包含了丰富重要的信息。当轴承发生故障时，故障部位会成为一个激励源不断持续地产生冲击，包含的故障特征信息越多，得到的振动信号越具有明显的规律性和自相似性，熵值越小。

(2)每种状态取15组组成原始训练样本集：R60×20，其余作为原始测试样本集：R56×20。采用ILS对原始训练样本特征向量矩阵的所有特征值依照重要性进行排序，其排序前如图5所示，排序后的特征值重要性顺序如图6所示。

由图5和图6可以看出，ILS排序前四类样本的前几个特征值非常靠近，而且有交叉现象。而采用ILS依据特征重要性进行排序后，四类样本的特征值在前几个维度上分的很开，没有交叉现象，这说明了采用ILS可以选取出区分不同状态内在信息的特征值。

图3 MSE和IMSE对比分析(误差条代表熵值的标准差)

图4 四种状态轴承振动信号的时域波形(从上到下分别为：NOR，ORF，IRF，BEF)

图5 四类状态的改进多尺度熵

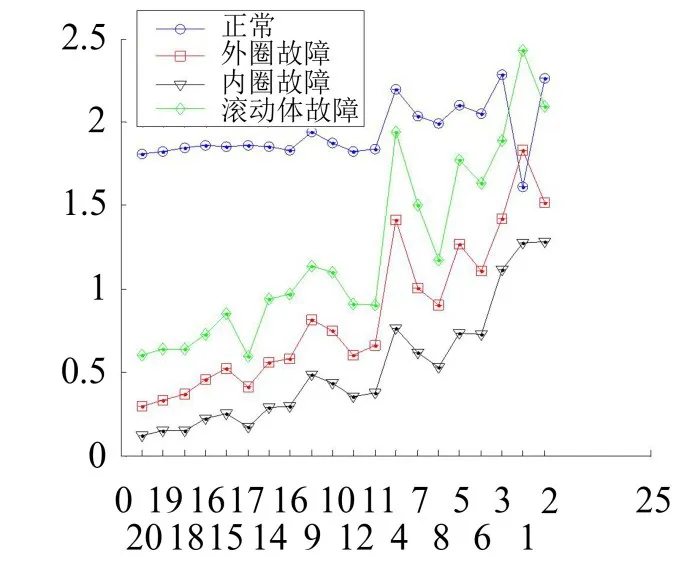
图6 采用ILS依据得分高低进行特征排序

将得分较高的前5个序列对应的特征值作为低维敏感故障训练样本特征集：R60×5。从原始测试样本集中选择与训练样本特征集中特征序列相同的特征值作为测试样本特征集：R56×5。

(3)采用训练样本特征集对基于VPMCD进行训练，建立预测模型VPM45；

(4)用训练好的VPM模型对测试样本集进行分类预测，根据输出结果来确定滚动轴承的工作状态和故障类型。预测的输出结果如图7所示，第一类表示正常，第二类表示外圈故障，第三类表示内圈故障，第四类表示滚动体故障。

由图7可知，所有测试样本类别都得到了准确的分类，论文提出的方法对测试样本集的识别率达到100%，这说明了论文方法的有效性。

图7 测试样本预测结果

为了说明IMSE方法在特征信息提取方面的优势，提取四类状态原始信号的MSE如图8所示以将IMSE与MSE进行稳定性对比。

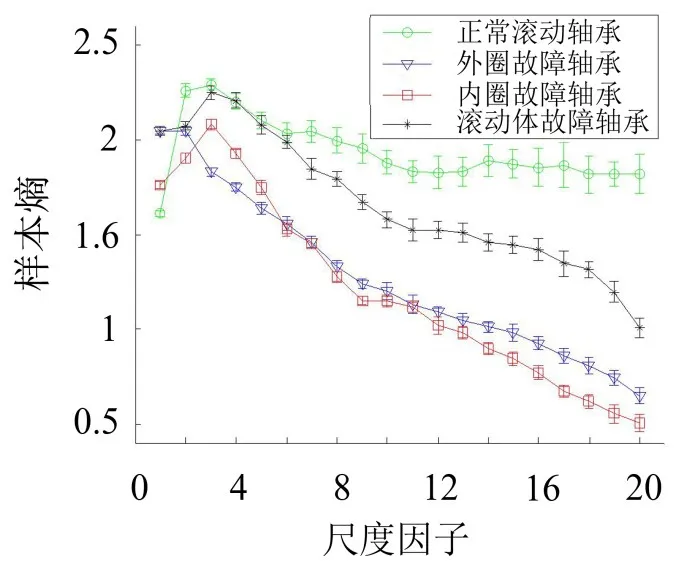
图8 四类状态的多尺度熵

从图8可以看出，在尺度因子较小时，特别地τ≤11时，四种状态的熵值很难区分，而只有当在较大尺度时，四类熵值才有明显的区分，对比图5的IMSE曲线可知，IMSE方法得到的四种状态的熵值曲线两两都能够明显区分开来，因此，IMSE方法在非线性、非平稳信号特征信息提取方面比MSE方法有优势。

从图8也可以看出，正常滚动轴承和滚动体故障状态下几乎所有尺度上的IMSE的标准差都小于MSE的标准差，对于外圈故障和内圈故障，在较大尺度上IMSE的标准差小于MSE的标准差，再者MSE的标准差曲线波动较大，随着尺度的增加有上升的趋势，而IMSE标准差曲线波动很小，随着尺度因子的增加几乎平稳或有下降的趋势。总体而言，采用IMSE方法得到的特征稳定性较MSE方法好。综上，IMSE方法无论在特征信息提取还是在稳定性与一致性方面都明显优于MSE方法。

为了说明进行ILS特征选择的必要性，采取MSE方法(其中τmax=20)对上述正常、外圈、内圈和滚动体故障四类状态振动信号提取特征后，一是采用ILS对其特征依照重要性进行排序，然后选取得分较高的前5个序列对应的特征值作为低维敏感特征；二是直接选择前5个作为低维特征。然而，分别输入到VPMCD中进行模式识别，两种不同方法的分类结果分别如图9(a)和图9(b)所示。

从图9(a)中可以看出，采用ILS方法四种类别全部得到了正确的分类，而从图9(b)中可知，正常状态中的第2、3、5、7、9、10、11、12和14组被错误地分到了滚动体故障中，错误率为64.285 7%，虽然其他三类都得到了正确分类，但总体识别率仅为83.928 6%

为了说明采用VPMCD分类的优势，分别采用VPMCD和BP神经网络对得到的特征集进行训练与分类预测，其中训练集样本和测试集样本数与本文上述相同，其分类预测结果如图10(a)和图10(b)所示。

从图10(a)中可以看出采用VPMCD方法，样本都得到正确的分类，识别率为100%。而从图10(b)中可以看出，内圈故障和外圈故障都错误地分到了其他类别中，虽然正常状态和滚动体故障得到了正确的分类，但总体识别率仅为50%。同时，两种分类方法耗时对比如表1所示。

从表1中可以看出，采用VPMCD方法的耗时要小于BP神经网络分类方法，且由上述分析知，采用VPMCD方法的正确识别率远大于BP神经网络。

图9 采用ILS方法(a)和未采用ILS(b)方法的分类结果

图10 VPMCD和BP神经网络预测结果

表1 两种分类方法的分类时间对比

3 结语

(1)针对MSE会随着粗粒尺度因子的增大而产生不精确的熵估计或未定义熵的缺陷，提出了IMSE方法，该方法克服了MSE的缺陷。通过仿真信号分析，将IMSE与MSE方法进行对比，结果表明了IMSE比MSE方法能够得到更精确的熵估计，稳定性和一致性更好。

(2)提出了一种基于IMSE、ILS和VPMCD的滚动轴承故障诊断方法，并将其应用于实验数据分析，结果验证了IMSE方法在提取特征信息方面的优势、ILS特征选择的必要性以及VPMCD分类器在正确识别率和耗时的优越性。

[1]司景萍，牛家骅，郭丽娜，等.信息熵和RBF神经网络的发动机故障诊断[J].噪声与振动控制，2015，35(1)：214-218.

[2]曾求洪，宾光富，李学军，等.基于小波包近似熵与LMS加权特征融合异步电机故障诊断[J].噪声与振动控制，2015，35(5)：139-144.

[3]郑近德，程军圣，杨宇.基于LCD和排列熵的滚动轴承故障诊断[J].振动、测试与诊断，2014，34(5)：802-806.

[4]邹龙庆，陈桂娟，邢俊杰，等.基于LMD样本熵与SVM的往复压缩机故障诊断方法[J].噪声与振动控制，2014，34(6)：174-177.

[5]郑近德，程军圣，杨宇.基于多尺度熵的滚动轴承故障诊断方法[J].湖南大学学报(自然科学版)，2012，39(5)：38-41.

[6]陈慧，张磊，熊国良，等.滚动轴承的MSE和PNN故障诊断方法[J].噪声与振动控制，2014，24(6)：169-173.

[7]ZHU L,MIAO L,ZHANG D.Iterative Laplacian Score for Feature Selection[M]//Pattern Recognition,2012:80-87.

[8]HE X,CAI D,NIYOGI P.Laplacian Score for Feature Selection[J].Advances in Neural Information Processing Systems,2005,18:507-514.

[9]XU J,MAN H.Dictionary learning based on laplacian score in sparse coding[C]//Machine Learning and Data Mining in Pattern Recognition-,International Conference, Mldm 2011,New York,Ny,Usa,August 30-September 3,2011.Proceedings.2011:253-264.

[10]LIU R,YANG N,DING X,et al.An unsupervised feature selection algorithm:laplacian score combined with distance-based entropy measure[J].IEEE,2009,3:65-68.

[11]LIAO B,JIANG Y,LIANG W,et al.Gene selection using locality sensitive laplacianscore[J].IEEE/ACM TransactionsonComputationalBiologyand Bioinformatics,2014,11(6):1146-1156.

[12]RAO R,LAKSHMINARAYANAN S.Variable predictive models-A new multivariate classification approach for pattern recognition applications[J].Pattern Recognition, 2009,42(1):7-16.

[13]http://csegroups.case.edu/bearingdatacenter/pages/ download-data-file.Bearing Data Center,Case Western Reserve University.

Fault Diagnosis of Rolling Bearings Based on Improved Multiscale Entropy and VPMCD

JIANG Zhan-wei,ZHENG Jin-de,PAN Hai-yang,PAN Zi-wei
(School of Mechanical Engineering,Anhui University of Technology,Maanshan 243032,Anhui China)

Multiscale entropy(MSE)is an algorithm for measuring the complexity of time series.However,in the coarse graining process of MSE,the shortened time series will lead to an imprecise and large fluctuation of the entropy estimation.In this paper,an improved multiscale entropy(IMSE)algorithm is proposed.On this basis,combining with the iterative Laplacian score(ILS)feature selection with variable predictive model based class discrimination(VPMCD),a novel fault diagnosis method of rolling bearings is proposed.Finally,the proposed fault diagnosis method is applied to analyze the experiment data of rolling bearings.Its results are compared with the existing methods.The results indicated that the proposed method can effectively identify the rolling state and fault types of the rolling bearings,and has much better diagnosis effect than the existing methods.

vibration and wave;multiscale entropy;feature dimension reduction;variable predictive model;rolling bearing;fault diagnosis

TN911.7；TH165.3

：A

：10.3969/j.issn.1006-1355.2017.03.031

1006-1355(2017)03-0156-06+172

2016-11-03

国家自然科学基金资助项目（51505002、51305046）；安徽省高校自然科学研究重点资助项目（KJ2015A080）

姜战伟(1990－)，男，安徽省界首市人，硕士生，主要从事振动信号分析处理，机械设备故障诊断研究。E-mail:1068076688@qq.com

郑近德(1986－)，男，博士，硕士生导师。E-mail:lqdlzheng@126.com