流体管道超声导波无损检测

张术臣,赵昕海，李鸿光，李富才

（上海交通大学 机械系统与振动国家重点实验室，上海 200240）

流体管道超声导波无损检测

张术臣,赵昕海，李鸿光，李富才

（上海交通大学 机械系统与振动国家重点实验室，上海 200240）

研究工程中流体管道的结构损伤识别技术具有现实的意义。以实现管道损伤定位为目的，探讨超声导波检测技术在流体管道的结构损伤识别中的可行性以及其识别精度。选择材料为20#碳钢的圆管为研究对象，根据频散方程利用数值法求解其各个模态频散曲线。以管中导波的传播原理为基础，从管中导波的模式、频散特征、避开截止频率、传播速度等方面因素选择激励信号，通过Abaqus有限元仿真分析导波在流体管道中的传播机理，利用概率密度函数法实现流体管道损伤定位。最后通过在管道上引入切槽损伤和孔损伤进行实验，对定位方法进行验证，实验结果与仿真分析基本吻合，证明了该方法的工程实用价值。

振动与波；超声导波；流体管道；概率密度法；损伤定位

随着工业化的不断进步,流体运输管道己成为工业生产中不可或缺的组成部分。石油天然气管道输送在社会生产生活中占有极为重要的战略地位，且其通常工作在比较特殊或恶劣的环境中，容易出现锈蚀、腐蚀、裂纹、破损等缺陷，随着时间增长损伤扩大加剧，结构承载能力减弱，严重时甚至造成巨大灾难。为保证结构的安全运行，需要对结构定期检修。传统的管道检测技术常有较大的局限性，基于超声导波的无损检测能够较准确地实现结构损伤定位[1–4]。

近些年来，流体管道导波检测的研究成果很多。Sinh和Plon等研究了圆柱壳内或是流体负载时轴对称波在圆柱壳中的传播特性，并计算得到了波在截面上的位移和应力振幅分布的数值解。Long等研究了掩埋的铁管中有水时基本导波模式的衰减特性，此研究的衰减是导波向管外（土壤）泄露的情况，不考虑由于黏性而引起的衰减。他得安在假设实频率和复波数的基础上，考虑了导波的衰减，分析了超声纵向导波在充黏液圆管中的频散特性，得到了导波各模式的本征解[5]。刘增华等研究了充水管道中纵向超声导波的传播特性，从理论上得到了充非黏性液体管道中纵向超声导波的频散方程[6]。于保华等对多层圆管纵向导波频散特性分析方法进行了研究，提出一种基于频散特性的外推分析方法，通过优化选取导波检测模式和频率来减少频散特性对圆管纵向导波探伤结果的不良影响[7]。陈正翔等研究了充液圆柱管壳中振动波的频散特性。王秀彦等采用分布式PZT传感器在管中激励和接收超声导波，选择具有单一频率的特定信号激励超声波，使其频散最小。

本文选择材料为20#碳钢，外径80 mm，内径69 mm的圆管为研究对象，以管中导波的传播原理为基础，从管中导波的模式、频散特征、避开截止频率、传播速度等方面因素选择激励信号的中心频率，通过有限元仿真模拟超声导波在自由管道、充水管道、充油管道中的传播特性及损伤识别能力，利用概率密度函数的方法实现不同工况下的损伤定位，最后通过在自由管道和充水管道上引入切槽损伤和孔损伤进行实验，验证仿真结果的可靠性，比较不同工况下的定位精度和误差大小。

1 选择激励信号

1.1 管中导波的模态

受到圆柱体边界条件约束，横波与纵波相互作用，波的特征较复杂。基于超声导波的管道结构损伤检测，通常优先选用纵向导波和周向Lamb波。

1.2 管中导波频散曲线

圆管结构的纵向导波和周向Lamb波频散方程分别为

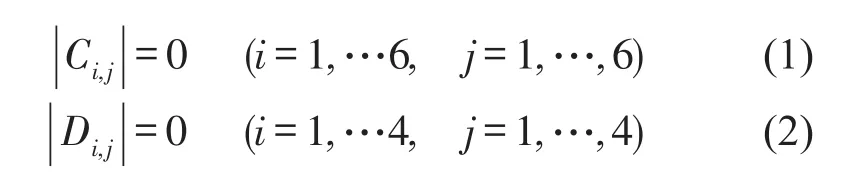
本次实验用材料为20#，外径80 mm，内径69 mm的圆管（E=210 GPa，ν=0.3，ρ=7 800 kg/m3）的频散曲线如图1、图2所示。

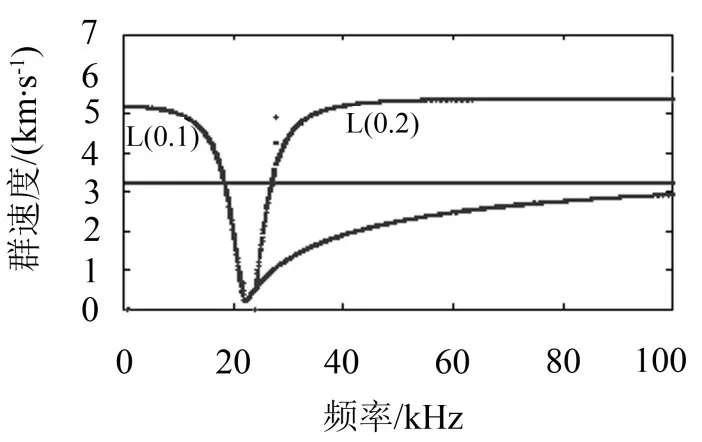
图1 纵向模态导波频散曲线(0～100 kHz)

1.3 避开截止区域

激励频率要避开截止频率附近区域，否则导波

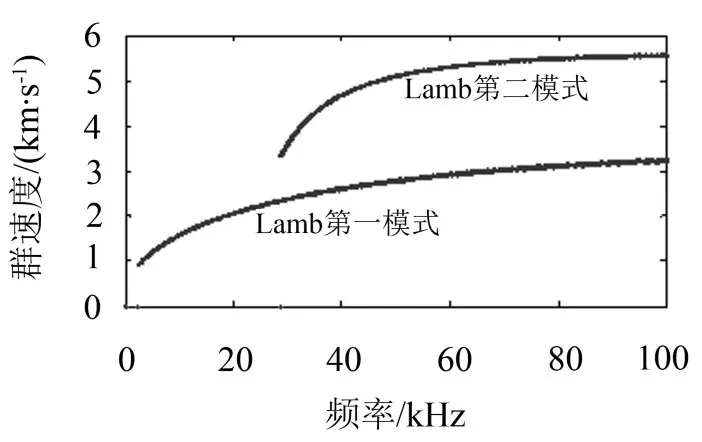
图2 周向Lamb波频散曲线(0～100 kHz)

群速度较小，或者随着传播距离增加导波幅值迅速衰减，不能远距离传播。如图1所示。纵向模态L(0,1)具有明显的“低通”特性，即频率较低时群速度较大，而L(0,2)具有明显的“高通”特性，即频率较低时群速度较小。L(0,1)模式低通截止频率flp与L(0,2)模式高通截止频率fhp分别为

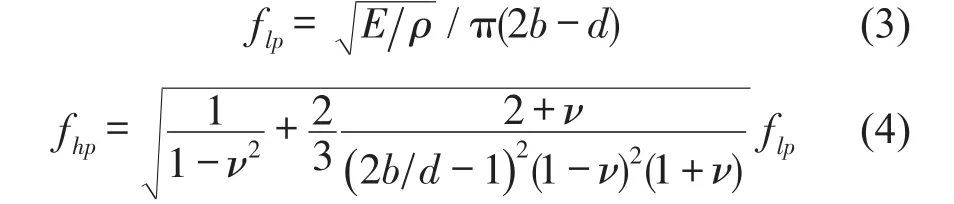
代入相关参数可得，flp=22.2 kHz，fhp=23.4 kHz。为避开截止频率，选择的激励频率应小于22.2 kHz或大于23.4 kHz。

1.4 速度重合点

图1中，L(0,1)模式群速度先迅速减小后逐渐增大，频散特性较明显。激励频率在60 kHz～100 kHz范围时，L(0,2)模式频散较小，有利于保证导波传播时速度的一致性。图2中，在能够激发出Lamb波的频率范围，60 kHz～100 kHz区间的两模式频散都不明显，第二模式略优于第一模式。

因激励方式为单点激励，导波沿轴向和周向同时传播，损伤定位要求轴向和周向同时定位，当激励的纵向导波和周向Lamb波在该测试圆管中有相等的速度时，定位最准确。故求取其速度重合点。

如图3所示，激励频率为63 kHz时，导波在此实验管道中激发的L(0,2)模式和Lamb波第二模式群速度重合，同为5 370 m/s。在此激励频率下，其他模式的群速度和该重合点速度均相差较大，便于不同模式的波包分离。

图3 L(0,2)和Lamb第二模式速度重合点

1.5 激励信号选择

为减少各个波包重叠程度，提高损伤的识别分辨能力，应减小激励信号的周期数目，但此举将引起激励信号频域主瓣变宽，不利于抑制导波频散效应。综合以上两方面因素，选择经汉宁窗调制的频率为63 kHz、周期数为3.5的正弦信号激励。

2 有限元仿真

2.1 建立有限元模型

本算例，管中流体的材料属性由EOS状态方程定义，选择状态方程中Us-Up形式，定义水的材料属性为：声速c0=1 483 m/s，密度=1 000 kg/m3，动力黏度=0.001Pa∙s。流体为原油时，定义原油的材料属性：声速c0=1 477 m/s，密度=934 kg/m3，动力黏度= 0.05Pa∙s。

使用Abaqus的显示求解器Explicit，选择Hex六面体单元类型，三维实体八节点缩减积分单元（C3D8R Element）划分网格。

如图4所示，在Abaqus仿真模型中设有一个激振器A和四个传感器S1－S5。通过在A处施加集中力，模拟中心频率为63 kHz、加汉宁窗的3.5周期正弦曲线激励信号，同时在S1－S5接收信号。

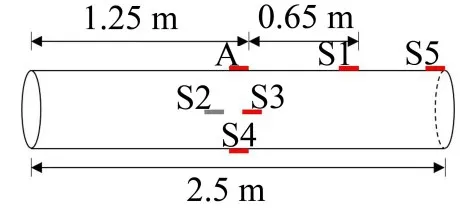
图4 激振器与传感器分布

将仿真所得自由管道、充水管道工况下，S1传感器的输出信号用小波变换重构，再用低通滤波器滤波，最后用Hilbert变换求取包络线，得出800 μs内无损伤条件下轴向方向正应力归一化后的历程输出波形如图5、图6所示。

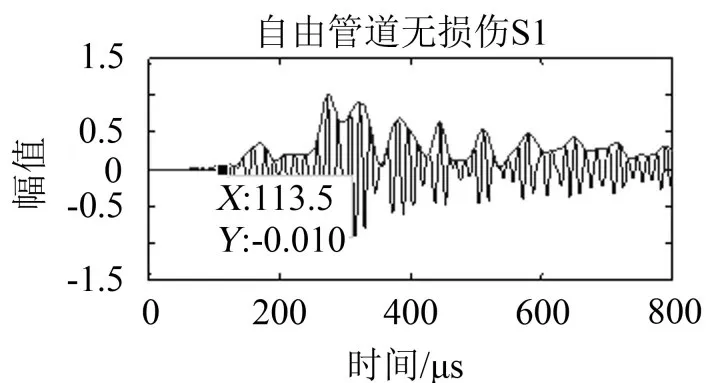
图5 自由管道S1的历程输出

图5、图6显示，两种工况下的S1输出有些许差别。导波在流体管道中传播时，弹性波透射到流体介质中导致一部分能量被流体吸收，吸收比率随传播距离的增大而增大，使接收信号幅值随时间逐渐衰减。L(0,2)模式和周向Lamb波以面内位移为主，使其能量衰减程度低于其他模式，飞行时间更加精确。以归一化后幅值的绝对值大于0.01时对应的横坐标作为波包的飞行时间，分别为113.5 μs和114.1 μs。用飞行距离0.65 m除以波包速度5 370 m/ s，得到理论波包飞行时间121.0 μs，和仿真波包飞行时间基本吻合，且充水管道工况下的飞行时间更加接近理论波包飞行时间。

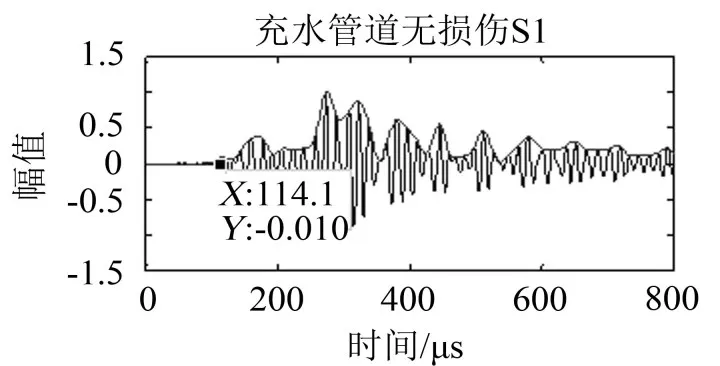
图6 充水管道S1的历程输出

2.2 概率密度法的原理

将损伤前后的导波信号作差，由差信号第一个波包的飞行时间确定损伤信号在圆管结构中的传播距离,如图7、图8所示。

图7 自由管道S1损伤前后差信号

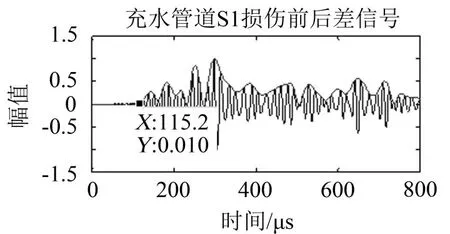
图8 充水管道S1损伤前后差信号

由此得到以激振器和传感器为焦点，以传播距离为长轴长的椭圆，为确定损伤位置，需要3个椭圆轨迹的交点，3个椭圆的焦点之一均是A，另一焦点从S1－S5五个传感器中选取，如图9所示。

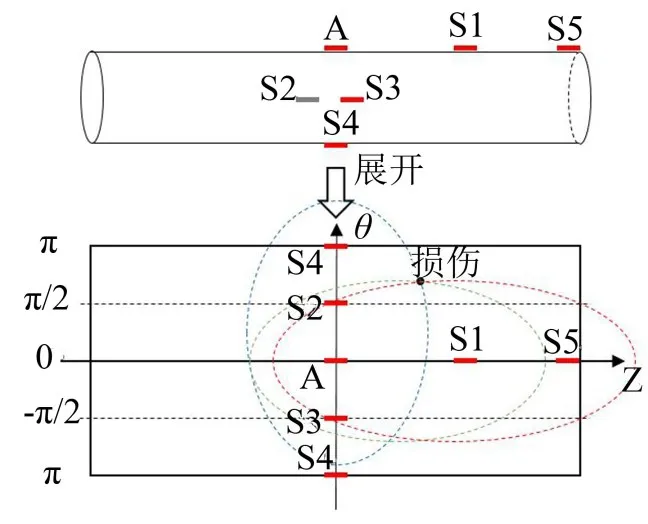
图9 椭圆相交轨迹

将圆管展开，对于第k条传感路径，导波由作动器(坐标为(zA,θA))经损伤所在位置(坐标为(z,θ))传递到传感器(坐标为(zSk,θSk))，飞行时间为tk，两种模式导波的共同速度为vg，由此确定损伤轨迹为

如果令ak为由该传感路径确定的椭圆长半轴长度，ck为该椭圆的焦距，bk为由该传感路径确定的椭圆短半轴长度，θk为经过作动器与传感器的直线与z轴方向的夹角；(zok,θok)为该椭圆的中心，分别为

由式(7)－式(8)整理可得由该传感路径确定的损伤轨迹方程为

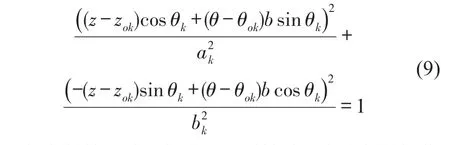
在实际情况中，由于ToF不精确，以及实际损伤并非点损伤，椭圆通常没有共同交点，所以采用概率密度的方法，实现损伤定位。距损伤轨迹越近则存在损伤的可能性就越大，反之则越小。融合多个椭圆轨迹，通过此方法即可获取不同位置的存在损伤的概率。定义相对距离函数δk(z,θ)，表示在第k条传感路径中，任意一点(z,θ)到损伤轨迹的相对距离

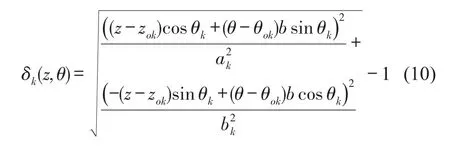
δk(z,θ)＜0表示该点在椭圆内，δk(z,θ)=0表示在椭圆上，δk(z,θ)＞0表示在椭圆外。

根据该传感路径，定义关于相对距离的正态分布概率密度函数fk(z,θ)，方差为σ，其表达式为

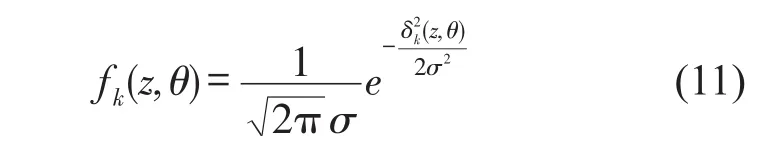
由式(10)－式(11)可知，当点在轨迹上时存在损伤的概率最大，各点的概率密度与该点到轨迹的相对距离δk(z,θ)成指数型衰减。

由于圆管轴对称，导波可以绕周向一直传播，所求得的椭圆轨迹有可能超出展开范围，对此可根据初步判断的损伤位置选择正确的传感器组合。当t2＜t3时，初步判断损伤位于一区或二区，选择坐标为p的S4和S1、S5定位；当t2＞t3时，损伤位于三区或四区，选择坐标为-p的S4和S1、S5定位。

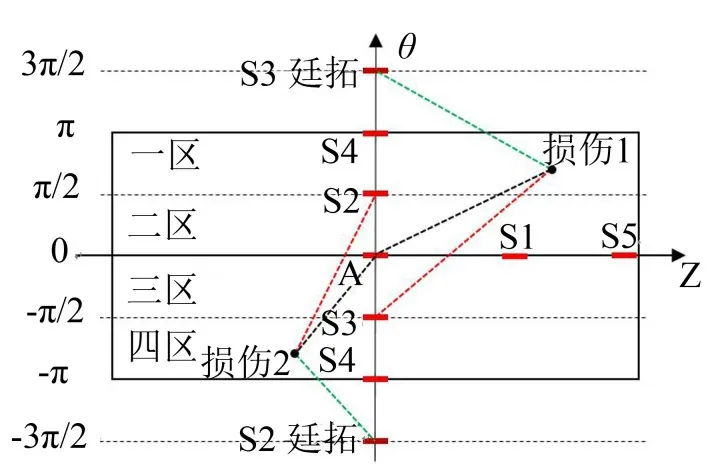
图10 圆管展开图分区

几何平均法得到的损伤概率密度最大值点主要取决于各传感路径相距距离函数的平方和，σ的取值对定位影响较小，采用该方法获取各点损伤概率密度相对大小为

其中N为传感路径总数。

获取各点存在损伤的概率密度相对大小，作归一化处理，得概率密度极大值点，如图11所示。

图11 概率密度定位图解

因管道的长径比很大，A与S1、S5构成的椭圆扁率很大，而A与S4构成的椭圆扁率很小，近似于圆，不能很好发挥在周向的辨识作用，故得出的概率密度图像有两个明显的极大值点，两点大致关于z轴对称分布。为排除干扰点，可在初步判断损伤区域时将排除掉的另一半区域概率密度赋值为零。

2.3 有限元仿真分析

在3种工况下模拟圆管损伤后的定位，损伤包括切槽损伤和孔损伤两种，切槽损伤通过删除单元格实现。其大小和位置可由3个参量表征，分别是距A的轴向距离d/mm、与A在周向的夹角α/(°)、切槽的弧度β/(°)。得出的8组仿真数据如表1所示。

空管在(400，30，30)切槽损伤算例下的概率密度成像结果如图12所示。

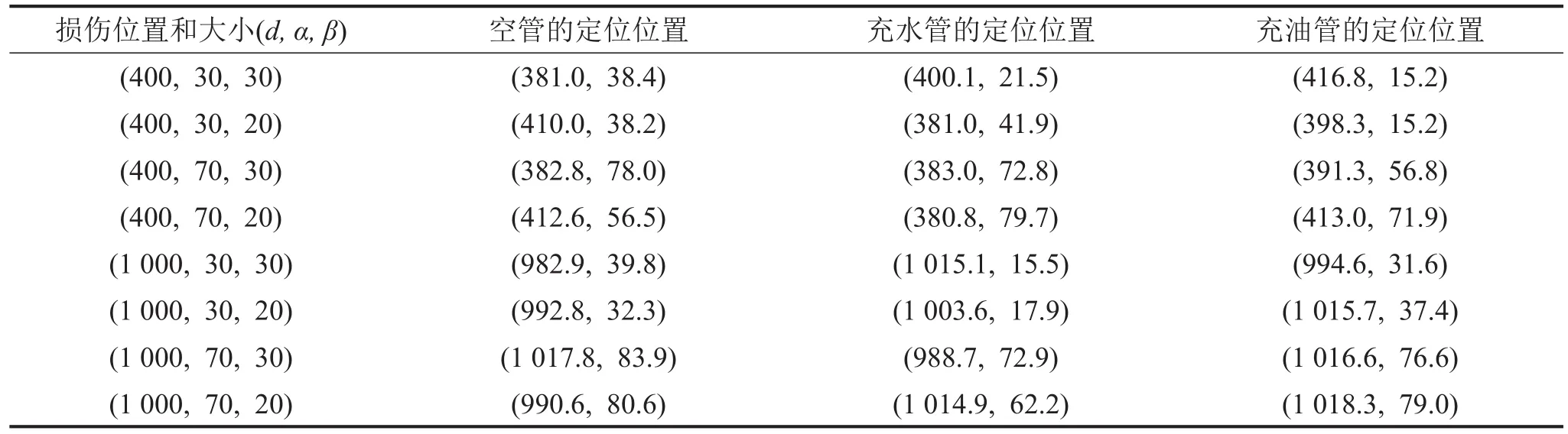
表1 切槽损伤定位结果

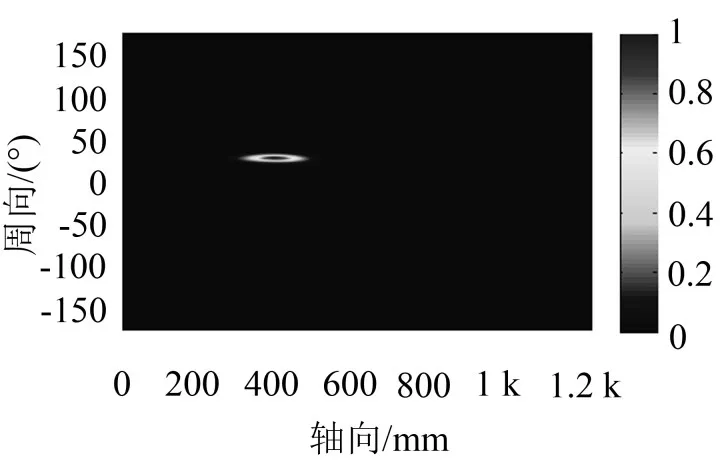
图12 切槽损伤下的概率密度成像

由表1可知在(400,30,30)切槽损伤算例中，概率密度极大值点为(381.0,21.5)，轴向定位绝对误差19.0 mm，周向定位绝对误差8.5°，如果以检测区域轴向范围1 250 mm为参照，轴向定位相对误差为1.52%，以检测区域周向范围360°为参照，周向定位相对误差为2.36%。

对3种工况下的定位误差进行统计，如表2所示：

(1)轴向定位误差比周向定位误差小，定位精度高。

(2)3种工况对比，充水管和充油管的定位精度相近，后者略优于前者，但两者均优于空管。

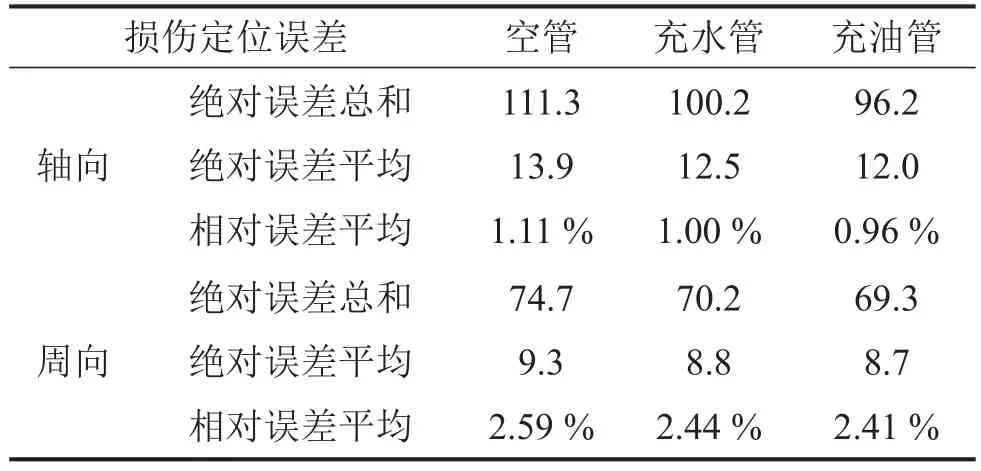
表2 切槽损伤定位误差统计

设计8个孔损伤，在3种工况下模拟圆管损伤后的定位，损伤大小和位置由3个参量表征，分别是距A的轴向距离d/mm、与A在周向的夹角α/°、孔直径Φ/mm。得出8组仿真数据如表3所示。

充油管在(550,75,4)孔损伤算例下的概率密度成像结果如图13所示。

图13 孔损伤下的概率密度成像

由表3可知在(550,75,4)孔损伤算例中，概率密度极大值点为(555.8,63.2)，轴向定位绝对误差5.8 mm，周向定位绝对误差11.8°，轴向定位相对误差为0.46%，周向定位相对误差为3.28%。

对3种工况下的定位误差进行统计，如表4所示。

3 实验验证

实验现场布置如图14。

图14 实验现场布置

实验数据由于受到环境噪声和电磁干扰的影响，直接进行Hilbert变换会有很多毛刺，这些毛刺会影响波包飞行时间的判断。在希尔伯特变换之前先使用示波器采样平均功能对信号平均处理，再使用小波变换对采集信号进行重构，可有效减小实验误差。

在空管和充水管道两种工况下对实验圆管施加切槽损伤，损伤位置和大小为(400,150,30)，即与A轴向距离为400 mm，周向夹角150°，切槽弧度30°。取512组损伤信号的平均值与512组无损伤信号的平均值作差，经过小波变换重构，采用概率密度法进行损伤定位，定位结果如图15。

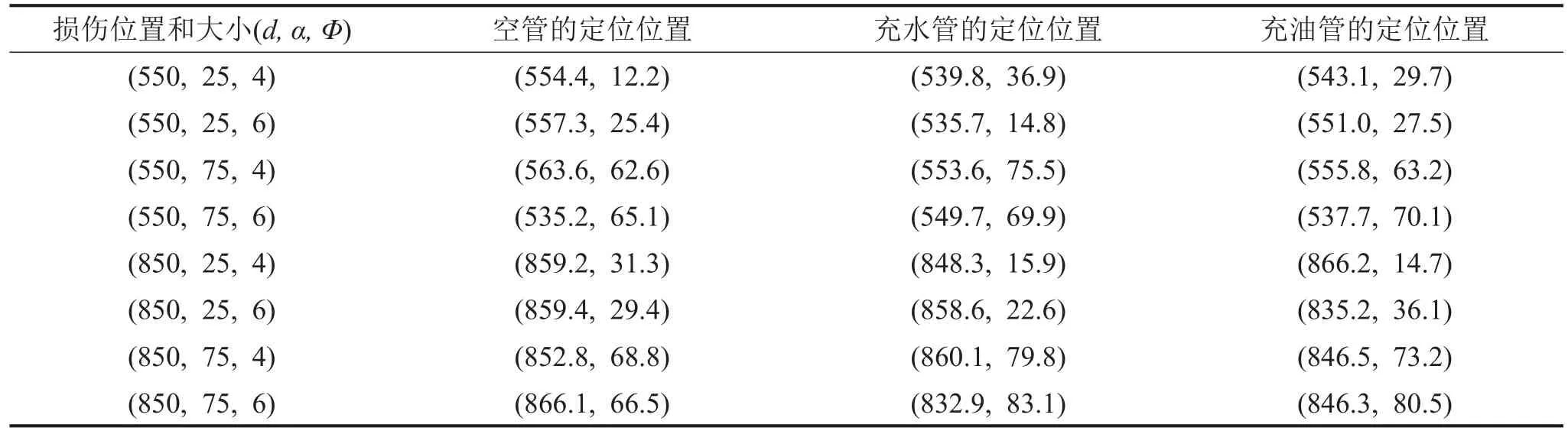
表3 孔损伤定位结果

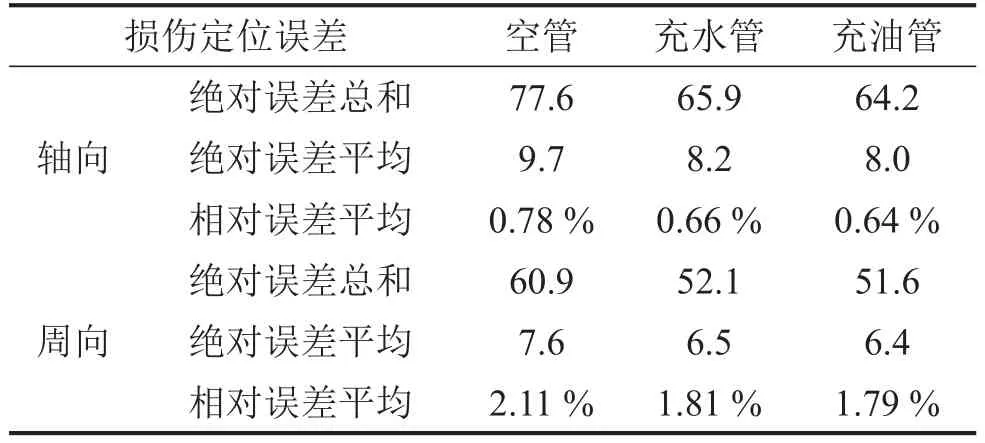
表4 孔损伤定位误差统计

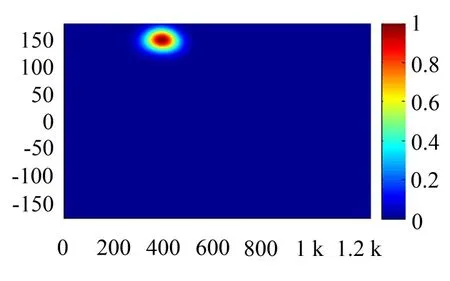
图15 槽损伤实验的概率密度成像

空管的概率密度最大值点为(427.9,162.5)，轴向定位绝对误差为27.9 mm，相对误差为2.23%，周向定位绝对误差为12.5°，相对误差为3.47%，周向定位误差比轴向定位误差大。充水管的概率密度最大值点为(416.3,158.7)，轴向定位绝对误差为16.3 mm，相对误差为1.30%，周向定位绝对误差为8.7°，相对误差为2.42%，定位误差比空管小。

同样，在两种工况下对圆管施加孔损伤，损伤位置和大小为(500,25,4)，空管和充水管的概率密度最大值点分别为(523.8,35.5)和(515.1,32.2)，轴向相对误差分别是1.90%、1.21%，周向相对误差分别是2.80%、2.00%，充水管的定位误差仍比空管小。

实验中的各工况下定位结果与仿真基本吻合，证明用概率密度法定位损伤是可行的。定位精度的差别对比和仿真相同，即充满流体的管道比空管定位精度高。

4 结语

(1)概率密度法在圆管损伤定位中误差较小，定位精度较高，有很高的工程应用价值。

(2)周向定位误差比轴向定位误差大，与实验圆管的长径比较大有关。

(3)管中充满液体时定位误差比空管小，定位精度随液体黏度的增大略有提高。

(4)在工程实际应用中，进行输水管道和输油管道的超声导波损伤定位时，无需排掉管中流体，直接在管道充液状态下检测能提高定位精度。

[1]YAN F,ROYER R L,ROSE J L.Ultrasonic guided wave imaging techniques in structural health monitoring[J].Journal of Intelligent Material Systems and Structures, 2010,21(3):377-384.

[2]MICHAELS J E,LEE S J,CROXFORD A J,et al.Chirp excitation of ultrasonic guided waves[J].Ultrasonics, 2013,53(1):265-270.

[3]VISHNUVARDHAN J,MURALIDHARAN A, KRISHNAMURTHY C V,etal.Structuralhealth monitoring of anisotropic plates using ultrasonic guided wave STMR array patches[J].Ndt&E International, 2009,42(3):193-198.

[4]DE MARCHI L,MARZANI A,CAPORALE S,et al. Ultrasonic guided-waves characterization with warped frequency transforms[J].IEEETransactionson Ultrasonics,Ferroelectrics,and Frequency Control, 2009,56(10):2232-2240.

[5]他得安.充黏性液体管材中超声导波的应力分析[J].声学技术，2006，25(5)：419-425.

[6]刘增华，何存富，杨士明，等.充水管道中纵向超声导波传播特性的理论分析与试验研究[J].机械工程学报，2006，42(3)：171-178.

[7]于保华，杨世锡，甘春标.一种多层圆管纵向导波频散特性分析方法研究[J].工程力学，2013(4)：373-379.

Fluid Pipe Nondestructive Testing Based on Ultrasonic Guided Waves

ZHANG Shu-chen,ZHAO Xin-hai,LI Hong-guang,LI Fu-cai
(State Key Laboratory of Mechanical System and Vibration,Shanghai Jiaotong University, Shanghai 200240,China)

Structural damage identification technology for fluid pipes is highly practical in engineering field.For the purpose of realizing the pipeline damage localization,the feasibility and recognition accuracy of the ultrasonic guided wave testing technique in fluid pipes are discussed in this study.A pipe made of 20#carbon steel is used to investigate the damage localization.According to dispersion equations,numerical method is applied to obtain various modal dispersion curves. Based on pipe wave propagation theory,and considering the influences of pipe wave patterns,dispersion characteristics and propagation velocity and the requirement of avoiding the truncated frequency,the excitation signals are selected.The guided wave transmission mechanism in the fluid pipes with different fluids is analyzed numerically by means of ABAQUS software.The method of probability density function is applied to realize fluid pipe damage localization.Finally,notches and holes are introduced to the fluid pipe in the experiment to verify the effectiveness of the proposed method.The experimental results and simulation results are consistent.The engineering practical value of this method is proved.

vibration and wave;ultrasonic guided wave;fluid pipe;probability density method;damage localization

TH113.1；TB559

：A

：10.3969/j.issn.1006-1355.2017.03.040

1006-1355(2017)03-0197-06

2017-01-06

国家自然科学基金资助项目(11427801)

张术臣（1992－），男，山东省潍坊市人，硕士生，主要研究方向为结构健康监测。

李鸿光，男，博士生导师。E-mail:hgli@sjtu.edu.cn