车用交流发电机电磁振动噪声预测研究
赵汝炫,董大伟,闫 兵,张胜杰,唐 琴
(1.西南交通大学 机械工程学院,成都 610031;2.成都华川电装有限责任公司,成都 610106)
车用交流发电机电磁振动噪声预测研究
赵汝炫1,董大伟1,闫 兵1,张胜杰2,唐 琴2
(1.西南交通大学 机械工程学院,成都 610031;2.成都华川电装有限责任公司,成都 610106)
为了从发电机设计之初就能精确预测其振动和噪声,进而进行优化设计,需要建立一个电磁振动噪声预测分析模型。以一台36槽6极对的爪极发电机为研究对象,利用有限元法计算作用在定子铁芯上的电磁力,再耦合到电机结构模型中计算瞬态电磁振动,最后将电机振动响应作为声学边界条件,利用时域边界元法计算出电机的辐射噪声。计算表明该发电机的电磁振动噪声频率以36谐次为主,与实验测试的噪声频谱分布相同,两者最大声压级相差2.9 dB,实现了较高精度的电磁振动噪声预测分析,对发电机NVH研究具有指导意义。
声学;噪声预测;有限元法;电磁力;电磁噪声;时域边界元法
汽车整车NVH一直是近年来研究的热点,而随着乘客对声振舒适性要求的提高,汽车零部件的NVH也引起了各大汽车整车厂和零配件厂商的广泛关注。其中发电机的噪声是汽车零部件噪声的一个重要组成部分。发电机噪声可以分为机械噪声、电磁噪声和空气动力噪声三个部分。研究表明,汽车发电机处于中低转速时电磁噪声显得尤为强烈,而面对城市复杂的交通状况,怠速、停车正是属于中低转速范围,因此研究发电机的电磁噪声尤为关键。
电磁振动噪声是由于变换的气隙空间磁场产生一个空间旋转力波,该力波使得定子和转子发生振动变形,振动传递到电机端盖上,从而辐射出噪声。影响电磁振动噪声的因素很多,其中主要包括定转子槽极配合、电机装配公差及电机的结构尺寸。精确预测和有效地减小发电机的电磁振动噪声成为发电机在开发和优化设计中的一个难点和热点。
发电机的电磁振动噪声预测涉及多个物理场之间的计算和数据传递,包括电磁场中激励源电磁力的计算、结构场中模态分析和振动的计算、声场中由振动引起的辐射噪声的计算。这种多物理场的计算在很多文献中已有研究。文献[1]中研究了永磁有刷直流电动机的电磁振动,建立了计算电机电磁力、振动和辐射噪声的数值模型,并分析了电机设计参数与电磁振动与噪声的关系。该研究只考虑了二维空间的电磁力计算,但实际电机中由于结构的因素,其沿轴向分布的电磁力是不一致的,应当扩展到三维空间中进行电磁力的计算。文献[2]建立了永磁同步电机的电磁和结构弱耦合的有限元模型,通过Ansys参数化建模,完成电机电磁力的求解,最后耦合到结构有限元模型中,求得电机定子上任意一点的振动情况。该研究没有涉及辐射噪声的计算。文献[3]指出当径向电磁力的空间模数为0时,由其产生的振动最大。文献[4]研究了圆柱状电机模型的电磁振动噪声特性,指出径向电磁力的模数与引起的振动模态数是一致的,模数为多少,引起的振动模态数也为多少。文献[5]建立了电磁振动噪声的多物理场有限元模型,预测了电磁振动噪声的特性,并与实验结果对比,具有较好的一致性。目前大量研究还局限于二维电磁力的分析计算及其引起的振动,三维电磁力的计算和辐射噪声相对研究较少,因而不易实现电磁振动噪声精确预测。本文以某型号爪极交流发电机为研究对象,详细地介绍了电机电磁振动和噪声预测的数值仿真过程,分析了产生电磁振动噪声谐次的原因,实现了较高精度的电磁振动噪声预测分析。
1 电磁力计算
1.1 理论基础
发电机电磁力按其影响可分为切向电磁力(电磁转矩)和径向电磁力。电磁转矩是电机齿槽效应所引起的磁阻力矩,该力矩会对发电机的原动机输入轴产生一个阻力,同时作用在定子齿上使其产生形变。单相电机或者电机结构不对称时,会产生比较大的切向振动,容易引起电机相连部件的共振,产生辐射噪声。径向电磁力是由于电机的主磁通大致是沿径向进入气隙,因而在定子和转子上产生径向力,从而引起电磁振动和噪声。大量文献表明径向电磁力是产生电磁振动的主要原因,但也不能忽视切向电磁力的影响,因此本文在后续计算中将同时考虑这两个方向电磁力的影响。
发电机电磁力的计算通常有解析法、等效磁网络法和有限元法。解析法适合二维电磁力分析,其物理意义明确,但得到的表达式较为繁琐。等效磁网络法通过磁通管原理,把发电机内部磁通密度相对均匀的部分看作一个单元,最后再把各个节点用等效磁导连接起来构成一个磁导的网络图,再根据电路的基本解法求得各个节点的磁位,进一步求得电机的参数和性能[6],但不易模拟饱和问题,同时还存在机械应力和结构上的问题。有限元法应用广泛,能较好地模拟三维发电机内部电磁场。本文采用有限元法来计算发电机的电磁力。
对于发电机的低频瞬态磁场,麦克斯韦方程组可以写为

式(1)中H为磁场强度,σ为电导率,E为电场强度,B为磁感应强度。
由式(1)可以得到

由式(2)可以求出磁场分布。再根据虚功原理,物体在n方向受到的力F为[7]

式中W——系统存储的总能量

式
(4)中V为分析场域的体积。
对于三维有限元,其单元为四面体,则物体在磁场中所受到的总力F可表示为

其中Ve为四面体单元的体积,单元的μe为相应材料的磁导率,Be为单元的磁感应强度。
1.2 仿真计算
采用Ansys Maxwell进行电磁力的分析计算。在Maxwell中建立发电机几何模型时,为了减少仿真时间,考虑到发电机结构和绕组的周期性,建立了1/6电机模型。其中爪极是将励磁绕组产生的轴向磁通转化为径向磁通的环节,其模型的准确性和材料的相对磁导率(B-H曲线)将影响有限元计算结果的可靠性和精确度,因此爪极模型先用三维建模软件Catia生成后,再导入到Maxwell中。在电磁场计算中,定子铁芯齿尖部分位于与空气交界的边界处,其网格大小对电磁力的幅值有较大影响,需进行网格加密处理以提高计算精度,具体的网格划分如图1所示。

表1 电机模型部分参数

图1 1/6电机网格模型
模拟发电机在满负载的的情况下,当转速为3 000 r/min工况时的电磁力计算,因此需要在三相绕组上引入外电路来模拟外负载,该方法称为场路耦合法。场路耦合法在模拟满负载工况的同时,能通过观测发电机的输出特性(输出电压和输出电流),并与额定输出特性相比较,来验证仿真模型的可靠性,外电路如图2所示。

图2 外电路图
仿真步长为0.1 ms,仿真总时长为20 ms(一个旋转周期),仿真计算得到的发电机输出电压和电流曲线如图3、图4所示。
由图3、图4可知,仿真计算的输出电压达到稳态时在13.5 V附近波动,输出电流在122 A附近波动;而查阅该型号电机在3 000 r/min的额定输出电压为13.5 V,电流为120 A。证明了电磁仿真模型的可靠性。
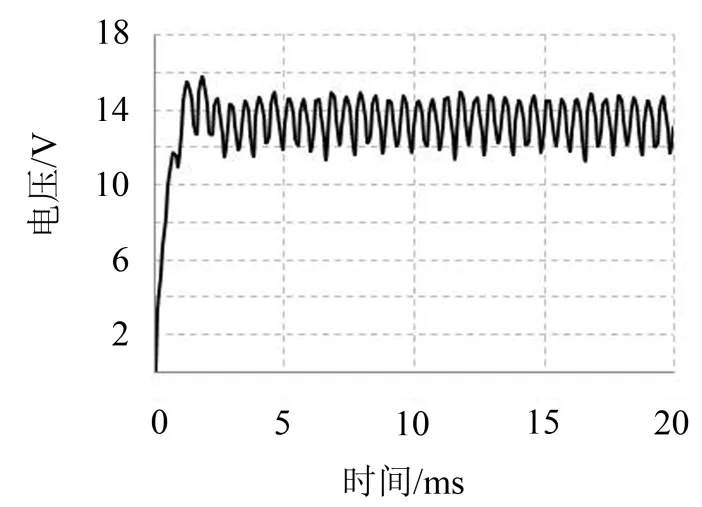
图3 输出电压曲线

图4 输出电流曲线
提取某定子齿上的三个方向电磁力的瞬态结果,进行傅里叶变换,得到各向电磁力频谱如图5所示。

图5 某定子齿上的各向电磁力频谱
由图5可知,径向电磁力占电磁力的主导地位,远大于切向、轴向电磁力。径向和切向电磁力在6、12、24、36谐次均有较大峰值,而轴向电磁力只在6谐次有较大峰值。为了更加贴近电机实际工作状态,在后续计算中,将三向电磁力均匀施加到电机的定子铁芯上。
2 电机结构模态和电磁振动计算
电机的振动系统是一个线性时变系统,运动方程为[8]

式中M为系统整体的质量矩阵,C为系统整体的阻尼矩阵,K为系统整体的刚度矩阵,F(t)为节点力矢量,u(t)为系统位移。
模态分析能找出发电机的固有频率,当激励力频率和固有频率相近时,会发生共振,因此模态分析相当关键。在Ansys Workbench中进行模态分析,通过设置电机各部件的材料参数、部件之间的接触状态及边界条件,网格大小划分为4 mm,计算发电机的模态。表2为仿真计算的前5阶模态频率与该型号发电机的约束模态实验的对比结果。

表2 仿真与实验径向模态结果对比
仿真与实验模态频率的误差在5%以内,这与文献[9]中的结果相比,具有较好的一致性,也验证了仿真模型的准确性。
由于发电机电磁场模型与结构有限元模型的网格划分不一致,因此求解出的节点力在载荷传递过程中较为复杂。本文考虑将三维电磁场仿真得到的三向电磁力通过均布的面力加载到电机定子铁芯上,实现载荷从面到面之间的传递,如图6所示。

图6 电磁力加载示意图
经过结构瞬态有限元计算,得到发电机的振动响应。图7为10 ms时发电机的振动速度响应云图,图8为前端盖上部某一位置节点的振动速度频谱曲线。

图7 10 ms时电磁振动速度云图
由图7可以看出,定子齿的部分振动能量传递到了发电机外端盖上,且外端盖径向上的振动速度幅值相比与外端盖端面部位较大,从侧面验证了径向电磁力是造成振动的主要原因。

图8 电磁振动速度频谱
由图8可知,振动主要在36、72谐次有较大峰值,其中36谐次的振动最大,其原因是36谐次的电磁力的空间模数为0。空间模数表示径向力在定子一周空间上分布有几个周期的正弦波。36谐次电磁力的模数理论上为36,36个旋转的正弦波作用在36个定子齿尖,无论在任何时刻,每个定子齿尖上受到的力都相等,相当于受到36个常力作用,因此其空间模数为0。空间模数越小,力谐波引起的振动越大,这与文献[5]所指出的结论相一致。同时36谐次电磁力的频率成分与电机整机的第3阶径向模态(1 763.5 Hz)十分接近,从而引起电磁共振,使得36谐次的振动急剧增大。
对于72谐次的振动,其电磁力的空间模数也为0,因而也会引起一定的振动。但由于其谐次较大,径向电磁力较小,则振动比36谐次的振动小。
3 电机辐射噪声计算
3.1 基本理论
发电机的声辐射问题可以通过求解一定边界条件下的波动方程来描述,分析方法有频域分析和时域分析。本文采用时域边界元方法来计算电机的瞬态声场。
假定流体介质是理想的声学介质,即流体是绝热、均匀和完全弹性的,且声场满足线性小振幅条件,此时声压p满足波动方程[10]

在无穷远处,还应该满足Sommerfeld辐射条件

对于有密闭边界面的外声场问题,外场任意位置处的声压可表示为

式中Ωa为边界面为边界面处声压为格林函数,对于坐标系原点选在|r⇀-r⇀a|=0,格林函数为边界面外法线方向。
3.2 仿真计算
本文模拟计算半消声实验室条件下,发电机声场的辐射特性。瞬态边界元法是将结构有限元求解出的振动结果通过插值的方法映射到声学边界元网格上作为边界条件,进行噪声辐射计算。在结构有限元网格的节点数据映射到声学边界元网格的节点上时,为保证数据在映射过程中的有效性,建立的边界元模型需要与电机的表面模型尽可能相贴近。忽略发电机内部的振动的影响,以电机的端盖外表面作为建立边界元模型的基础。
为了得到密闭的边界面,在LMS Virtual.lab中将电机的有限元模型进行提取面网格、填充特征孔洞、粗化表面网格等前处理。由于分析频率到5 000 Hz已满足本文的研究要求,而声学网格的最大单元边长要不大于计算频率范围最短波长的1/6,即声学网格单元长度满足L≤c/(6f),计算出声学网格单元最大可达到11 mm,本文取网格大小为8 mm,最终生成的密闭边界元三角形面网格如图9所示。

图9 声学边界元网格
根据GB/T 3767-1996《声学声压法测定噪声源声功率级反射面上方近似自由场的工程法》,建立直径为1 m的1/4球面场点。将电机的结构瞬态有限元计算结果导入LMS Virtual.lab中,利用时域边界元方法,计算电机的时域声学响应。图10为10 ms时的声压级云图,图中标注的5个测点为噪声观测点。

图10 10 ms时刻声压级云图
4 电机电磁噪声实验验证
为验证仿真得到的电磁噪声的合理性,需进行发电机噪声实验测试。实验麦克风布置如图11所示,测点位置与声场仿真的五个测点位置一致,分布在直径1 m的半球面上。

图11 实验麦克风布置
为减小发电机个体噪声差异导致的实验误差,选取5台同型号正常的发电机进行测试。测试电机在3 000 r/min满负载运行状态下的噪声。
图12为5台电机的五点平均实测噪声声压级频谱和声场仿真噪声的五点平均噪声声压级频谱对照曲线。

图12 仿真与实验平均声压级频谱对比
由图12可知,实验与仿真的峰值频率一致。在低频段,仿真的36谐次噪声峰值为70.1 dB,实验的36谐次噪声峰值为73.0 dB;在中高频段,仿真的72谐次与实验曲线也较为吻合,仿真的电磁噪声为55.2 dB,实验值为60.1 dB;在其他谐次,仿真与实验噪声的总体趋势也大致相同,该精度说明本次仿真较好地模拟了该型号电机的电磁辐射噪声。由于实验中存在部分机械噪声和因转子转动引起的空气动力噪声,因而仿真值略小于实验值。
对比图5、图8可以看出,从电磁力到电磁振动,力和振动的峰值频率不一致。这是由于36谐次和72谐次的电磁力的空间模数小,引起较大的振动,同时36谐次与发电机的第3阶径向模态频率相近而发生共振,从而导致该谐次的振动最大。而其他谐次的电磁力空间模数大,又与发电机的模态不匹配,因而振动较小。对比图8、图12可以看出,振动和噪声声压级峰值频率一致,这是由于振动和噪声声压级之间存在线性关系,而空气对于噪声传播过程中的频率影响可忽略不计。
5 结语
本文以某型车用交流发电机作为研究对象,用有限元法计算了电机电磁场产生的电磁力,并将其施加在电机整机模型上,计算了电机的瞬态振动,最后利用时域边界元法将得出的振动作瞬态声场分析,得出的结果与实验结果比较,两者最大声压级相差2.9 dB,实现了较高精度的电磁振动噪声预测分析。
研究表明,36槽发电机的电磁振动和噪声均在36谐次达到峰值,其原因是36谐次径向电磁力的空间模数为0,空间模数越小,力谐波引起的振动越大,同时36谐次电磁力的频率成分与发电机整机的第3阶径向模态十分接近,从而引起电磁共振,使得36谐次的振动噪声急剧增大。
[1]何鹄环.永磁有刷直流电动机电磁振动与噪声的分析[D].上海:上海交通大学,2012.
[2]杨浩东.永磁同步电机电磁振动分析[D].杭州:浙江大学,2011.
[3]LI XIAOHUA,HUANG SURONG,ZHANG QI,et al. Electromagnetic noise assessment for ev’s PM driving machines[J].2014,17 th International Conference on Electrical Machines(ICEM),2014:1552-1555.
[4]JEAN-BAPTISTE DUPONT,VINCENT LANFRANCHI. Noise Radiated by a Permanent Magnet Synchrnous Motor:Simulation Methodology InfluenceofMotor Defects[J].2014,17thInternational Conference on Electrical Machines(ICEM).2014:1321-1327.
[5]SHUANGLONG WU,SHUGUANG ZUO,XUDONG WU,etal.Numericalprediction and analysis of electromagnetic vibration and noise of claw pole alternator [J].Journal of Acoustical Society of America,2016,139 (4):2104-2104.
[6]陈军.具有永磁励磁的混合式爪极发电机的等效磁网络分析与计算[D].合肥:合肥工业大学,2003.
[7]戴魏,余海涛,胡敏强.基于虚功法的直线同步电机电磁力计算[J].中国电机工程学报,2006,26(22):11-114.
[8]高淑英,沈火明.振动力学[M].北京:中国铁道出版社,2011.
[9]张艺华.车用交流发电机电磁振动噪声特性及影响因素研究[D].成都:西南交通大学,2015.
[10]张海澜.理论声学[M].北京:高等教育出版社,2012.
Research on Electromagnetic Vibration and Noise Prediction for VehicleAlternators
ZHAO Ru-xuan1,DONG Da-wei1,YAN Bing1,ZHANG Sheng-jie2,TANG Qin2
(1.College of Mechanical Engineering,Southwest Jiaotong University,Chengdu 610031,China; 2.Chengdu Huachuan Electric Parts Co.Ltd.,Chengdu 610106,China)
In order to accurately predict electromagnetic vibration and noise at the beginning of alternator design for optimization,it is necessary to build a model for prediction of electromagnetic vibration and noise.In this paper,a 36s6p claw-pole alternator is researched.Finite element method is used to calculate the electromagnetic force acting on the stator. And the transient electromagnetic vibration is calculated by loading the electromagnetic force to the structural model. Finally,with the electromagnetic vibration results as the boundary condition,the boundary element method in the timedomain is used to calculate the electromagnetic radiation noise of the alternator.Results of calculations suggest that the 36-th order noise dominates the electromagnetic noise,which is well consistent with the experiment results.The error of the maximum SPL is only 2.9 dB.Thus,the results achieve high precision of noise prediction.This work gives the guidance to the NVH research of alternators.
acoustics;noise prediction;finite element method;electromagnetic force;electromagnetic noise;boundary element method in time-domain
TM301.4+3
:A
:10.3969/j.issn.1006-1355.2017.03.010
1006-1355(2017)03-0052-06
2016-12-06
赵汝炫(1991-),男,福建省福州市人,硕士研究生,主要研究方向为汽车噪声振动控制及声振舒适性。E-mail:617215169@qq.com
董大伟(1963-),男,成都市人,教授,博导,主要研究方向为汽车噪声振动控制及声振舒适性、内燃机振动噪声控制与故障诊断、车辆减振降噪及环境工程。E-mail:dwdong@swjtu.cn
通信作者:闫兵(1964-),男,成都市人,教授,硕士研究生导师,主要研究方向为机械设备与振动噪声控制、内燃机动力学、机械设备故障诊断系统。

