分段式结构对风力机塔架振动特性的影响分析

程友良，薛占璞，渠江曼，蒋 衍

（华北电力大学 能源动力与机械工程学院，河北 保定 071003）

分段式结构对风力机塔架振动特性的影响分析

程友良，薛占璞，渠江曼，蒋 衍

（华北电力大学 能源动力与机械工程学院，河北 保定 071003）

针对分段式结构引起的风力发电塔架失稳问题，利用刚体有限元法建立分段式结构三维动力学模型，提取模态分析的前五阶非零模态的振型，研究在湍流工况下分段式塔架连接处内外法兰的振型特性，通过内外法兰的振型与频谱响应对比，分析分段结构对塔架振动特性的影响。结果表明：分段式的外法兰比内法兰各阶振动位移量小，振动变化幅度小，不易发生共振，外法兰的第1阶振型起主导作用，非线性的扭转变形小，该结果可为塔架在运行过程中避免发生共振及失稳现象提供一定的参考。

振动与波；塔架；分段式结构；频谱；扭转变形

风力机塔架为分段式结构。塔架是整个风力发电机组的支撑部件，分段的塔架连接处分为内法兰和外法兰结构，法兰主要承受风的横向剪切及塔架的扭转等载荷作用，其振动特性直接关系到塔架结构可靠性和运行稳定性。张丰豪等利用刚体有限元方法对塔架进行三维结构动力学建模，通过浮动坐标系和坐标变换的基本原理，得出塔架1阶弯曲振动随着结构阻尼的增大主导作用减弱[1]。许斌等对混凝土填充钢箱的连接段进行弹性和弹塑性分析，发现连接段受力性能优于传统的法兰盘连接，传递载荷比较均匀[2]。王振宇等利用叶素理论，应用该风向突然偏转的工况，对塔架的应力分布进行分析，发现风向突然偏转90°时，塔架16.8 m高处发生屈服破坏[3]。柯世堂等利用谐波叠加法和改进的叶素动量理论并结合风振精细化频域计算方法有效模拟了叶片和塔架的脉动风速时程，发现离心力效应减小了塔架的风振系数[4]。应有等出了一种塔架主动阻尼控制方案，并通过技术仿真和现场试验对其控制效果进行了验证分析[5]。赵荣珍等运用次空间迭代法对塔架进行数值模拟，发现摆振是塔架的主要振动形式，1阶固有频率高于叶片通过频率[6]。程友良等对分段式塔架进行了数值模拟，发现分段式比锥筒式的应力变化幅度小[7]。黄珊秋等通过模态分析使塔架的尺寸和材料得到了优化优化设计[8]。张羽等从工程实用角度出发，总结了塔架的结构选型、屈曲特性及静动态特性等，并对塔架的未来研究趋势作出了展望[8]。吕钢根据多自由度模态分析理论，提出了弹性铰力学模型，发现振动的能量主要集中在第1、2阶频率处[9]。

在以往的研究中，通常只关注风力机塔架整体的风振效应，而塔架分段连接处的法兰振动情况研究甚少，法兰盘是各段连接的部件，对其进行振动特性研究直接关系到整个塔架的稳定性［10–13]，受实验条件所限,数值模拟成为研究分段式内外法兰的有效手段。研究一定工况下内外法兰的振动特性，结合模态分析，分析了分段式内外法兰对塔架的影响，该结果在一定程度上为避免塔架的共振及失稳现象提供参考。

1 数学模型

1.1 塔架分段式内外法兰数学模型

以某额定功率2 MW风力发电机塔架为研究对象，塔架采用内、外法兰两种连接方式，分别建立两个模型，内法兰外径4 837 mm，内径4 737 mm，厚度90 mm，外法兰与内法兰的几何尺寸相同，如图1为塔架内法兰，图2为塔架外法兰。材料为16Mn，密度为7 900 kg﹒m-3，弹性模量206 GPa，泊松比0.26。塔架内、外法兰三维结构动力学模型建立时，一般采用模态分析法或者有限元法，但这两种方法各有其不足之处，模态分析法建模时需要事先计算各阶固有频率及振型，一般考虑前2阶弯曲模态振型，而忽略了扭振及其他方向的振型情况。

对于小变形假设的有限元法不考虑各阶振型位移之间耦合作用。鉴于此，本文利用刚体有限元法对塔架分段式内外法兰进行建模，该方法采用浮动坐标和坐标变换，可以进行柔性部分大变形及各方向耦合的非线性计算。该方法的基本原理是是将柔性结构分割为由弹性阻尼节点连接的刚体单元，分别计算刚体单元的动能、重力势能以及弹性阻尼节点的弹性势能和阻尼耗散能，利用拉格朗日方程进行动力学建模[1]。其优点在于可计算任意变形范围内的振动，统一采用拉格朗日方程建模，还可以节省计算时间，在相同条件下，只需要有限元法的三分之一。图1为刚体有限元法示意图，图2为风力机塔架动力学模型，图3、图4分别为塔架外、内法兰结构动力学模型。

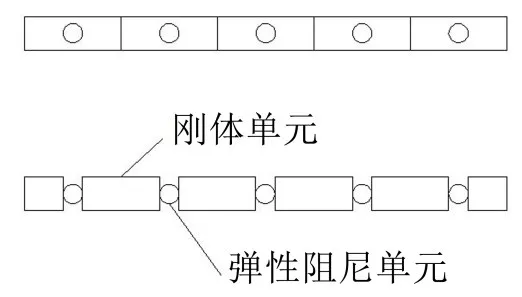
图1 刚体有限元法示意图

图2 风力机塔架动力学模型

图3 塔架外法兰

图4 塔架内法兰

1.2 基本控制方程

塔架内外法兰满足的基本控制方程，图2、图3中模型的3个平动位移（x1,x2,x3）和3个转动位移（φ1，φ2，φ3），将每个刚体单元的自由度统一用qi表示

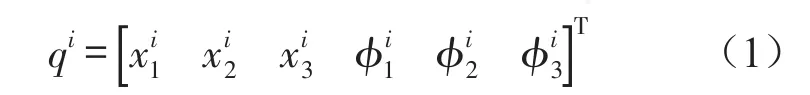
刚体单元中任意一点在参考坐标系中的位移可写为

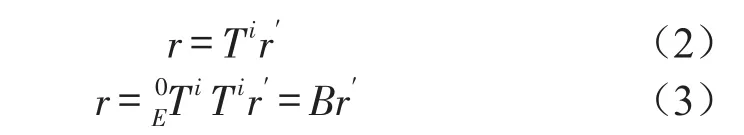
式中Ti——从坐标系{}′向坐标系{}的变换矩阵，

r′——固结坐标系{}′中的位置用矢量

r′表示，r——在坐标系{}中的位置用r表示，

刚体单元的动能为

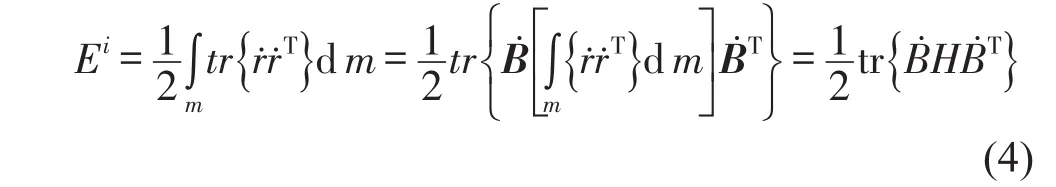
式中tr——矩阵的秩；B——坐标变换矩阵；变量上方加“.”——变量对时间的导数。

模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型［14–17]。具有n个自由度的无阻尼振动系统的振动微分方程可表示为

式中M——塔架结构的整体质量矩阵，

K——为塔架结构的整体刚度矩阵。

非零矢量ϕi的比例解为

将n个特征矢量ϕi按列排成n×n阶阵，可得系统的特征矢量矩阵

此时特征矢量为模态矢量或模态矩阵，即为模态振型。

2 计算工况及方法

2.1 边界条件及方法

为了对比塔架内外法兰振动特性，在塔高35 m法兰连接处施加50年一遇良态风，该脉动风风速波动值基本在±8 m/s范围内如图5。

塔架分为两段，法兰位于35 m处，塔高70 m，计算时间200 s，时间步长为10-5s，将塔架内外法兰的模态分析结果进行对比，分析其中的影响因素。

2 计算工况及方法

2.1 边界条件及方法

为了对比塔架内外法兰振动特性，在塔高35 m法兰连接处施加50年一遇良态风，该脉动风风速波动值基本在±8 m/s范围内如图5。

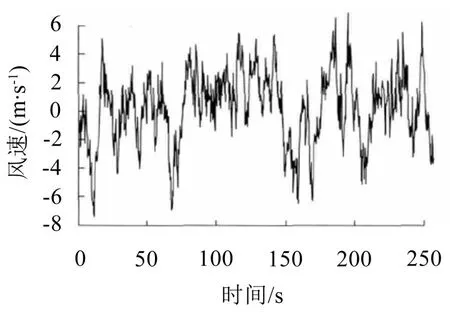
图5 塔高35 m处脉动风速（50年一遇）

塔架分为两段，法兰位于35 m处，塔高70 m，计算时间200 s，时间步长为10-5s，将塔架内外法兰的模态分析结果进行对比，分析其中的影响因素。

2.2 数值计算的准确性验证

为了保证数学模型的正确性与可靠性，进行对比验证。阻尼比为0.025时，将本文模型分段式的内、外法兰计算结果与获得认证的风力机结构计算程序FAST结果进行对比验证［18–20]。图6分别给出了内、外法兰横向位移对比结果，可得出本文模型与FAST计算程序的结果相吻合。塔架分段处的横向位移量约为0.1 m，与现实相符。

图6 塔架内外法兰横向位移对比

对分段式内法兰振动位移曲线进行快速傅里叶变换（FFT），利用获得的振动频率与有限元程序Bmode的计算结果进行对比，提取塔架的横向前五阶振动频率，如图7可知，本文内法兰分段式的振动频率小于计算机有限元程序Bmode的计算结果，误差较小，各阶振动频率相对误差在4%以内，充分证明了本文模型进行数值研究的可行性。

图7 振动频率对比

3 计算结果与讨论

3.1 分段式内法兰模态振型图分析

在塔架结构动力响应中，前5阶非零模态振型是所有振型的基础，与其对应的模态频率是振动特性分析的重点，确定塔架结构的模态频率直接决定塔架在什么范围内振动幅度较大。由图8可知，内法兰1阶模态振型（f=0.76 Hz）至5阶模态振型（f= 11.16 Hz），最大位移量为7.2 mm，前2阶振型中，看不出明显的扭转变形，第3、第4阶模态振型显示径向挤压振动并伴随扭转变形，第5阶显示横向扭转变形。由于在振动过程中，塔架的能量体现在前两阶振型对应的频率中，所以摆振是该内法兰的主要振型。当外加载荷频率和固有频率相同时，即发生共振现象。图7表明各阶振型位移量将提供共振参考，如，塔架内法兰振动测量的位移达到1.008 mm，对应的频率为0.76 Hz，此时将发生共振，应避免在该频率下运行。

3.2 分段式外法兰模态振型图分析

图9给出了分段式外法兰前5阶振型图，1阶模态振型（f=0.57 Hz）至5阶模态振型（f=12.24 Hz），最大位移量为6.06 mm，第3、第4阶模态振型显示径向挤压振动并伴随扭转变形，第5阶显示横向扭转变形，摆振依然是该外法兰的主要振型。对于塔架内法兰而言，外法兰在前5阶的频率分布及振动位移量均有优势。内法兰前5阶对应频率平均间隔为1.301 Hz，而外法兰为2.31 Hz，且各阶振动位移量比内法兰小。因此，外法兰塔架相对于内法兰塔架更不易发生共振，且振动变化小。

3.3 分段式结构对塔架振动特性的影响

根据图5边界条件，结合内外法兰结构动力响应，图10、图11给出了在不同频率下的频谱局部放大图，可以得出外法兰弯曲振动对应的高阶频率比内法兰少，并且变化幅度小，说明塔架在实际运行中，前3阶非零模态振型及频率对塔架的正常运行影响极大，甚至无需考虑第4、第5阶弯曲振动造成的影响。

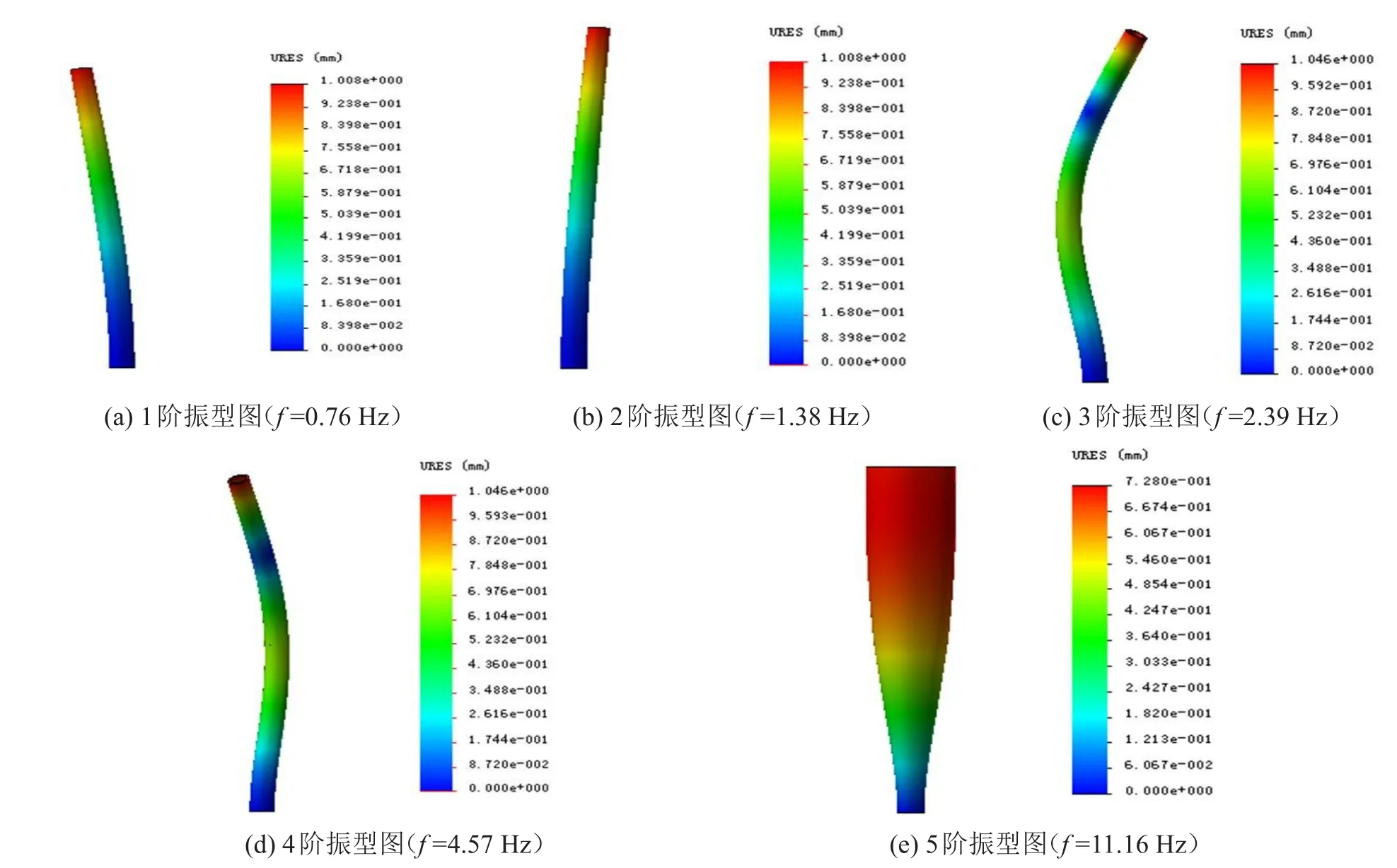
图8 内法兰前5阶振型图

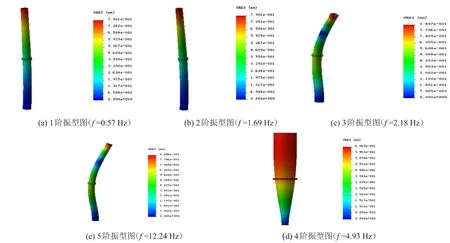
图9 外法兰前5阶振型图

图10 内法兰频谱局部放大

图11 外法兰频谱局部放大

从图10发现塔架随着频率的逐渐增大，内法兰塔架第1阶振动的主导作用逐渐减弱，振动特性主要源于外界湍流风的变化。在外湍流风变化极大的情况下，内法兰塔架的振动位移比对应的外法兰塔架位移量大，并且非线性作用占主导地位。内法兰极有可能在1阶振动频率发生共振，引起风力发电系统失稳。而外法兰相对于内法兰在1阶振动频率发生共振的几率小，因此应该避免该频率范围内引起的风力发电系统失稳现象发生。

4 结语

利用刚体有限元法建立塔架分段处内外法兰三维数学模型，进行结构动力学分析，研究了内外法兰在一定工况下的振动特性，并重点分析了内外法兰的振型变化情况，结论如下：

(1)外法兰的振动幅值相对于内法兰变化较小，振型中的位移量较小，摆振是内外法兰的主要振动形式，并且伴随轻微的扭转振动和弯曲振动，以前的研究注重塔架的弯曲振动，但随着柔性系统的发展，应该注重扭转振动的研究。

(2）内外法兰的1阶振型在塔架振动过程中起重要作用，其中非线性位移量是导致失稳的重要因素，外法兰相对于内法兰发生共振的几率小。

(3）内法兰弯曲振动的高阶频率比外法兰多，应增加以柔性系统为结构的减震装置，避免发生失稳现象。内法兰是比较传统的塔架连接方式，但是外法兰的振动特性优于内法兰，外法兰的结构优化及性能分析是未来研究的重点。

[1]张丰豪，何榕.结构阻尼对风力机塔架振动特性的影响[J].太阳能学报，2015，36(10)：2467-2473.

[2]许斌，李正超，谢咏剑.组合风电塔架混凝土填充钢箱连接段数值模拟[J].机械设计与制造，2016，(3)：30-33.

[3]王振宇，张彪，赵艳，等.台风作用下风力机塔架振动响应研究[J].太阳能学报，2013，34(8)：1434-1442.

[4]柯世堂，王同光，曹九发，等.考虑叶片旋转和离心力效应风力机塔架风振分析[J].太阳能学报，2015，36(1)：33-40.

[5]应有，朱重喜，杨帆，等.大型风电机组塔架主动阻尼控制技术研究[J].太阳能学报，2015，36(1)：54-60.

[6]赵珍荣，吕钢.水平轴风力发电机塔架的振动模态分析[J].兰州理工大学学报，2009，35(2)：33-36.

[7]程友良，薛占璞，渠江曼.新型分段式风力发电塔结构改进及性能研究[J].制造业自动化，2016，38(9)：45-49.

[8]张羽，蔡新，高强，等.风力机塔架结构研究概述[J].工程设计学报，2016，23(2)：108-123.

[9]吕钢.基于有限元法的水平轴风力机塔架动态响应与优化问题研究[D].兰州：兰州理工大学，2009.

[10]HUANG LINHONG,SONG LILI,LI GANG,et al. Variation Characteristics of Regional Synchronous Wind in Hami[J].Journal of Meteorological Research,2014, 29:344-357.

[11]WITTBRODT E,ADAMIEC-WÓJCIK I.Dynamics of flexible multibody systems:Rigid finite element method [M].Berlin:Springer,2006:5-82.

[12]黄珊秋，陆萍.ZONDZ-40风力机塔架的模态分析[J].太阳能学报，2001，22(2)：153-156.

[13]龙凯，贾娇.大型水平轴风力机塔筒涡激振动焊缝疲劳分析[J].太阳能学报，2015，36(10)：2455-2459.

[14]程友良，薛占璞，杨国宁.一种风力发电机塔架[P].中国专利：ZL201420777451.1，2015-06-17.

[15]戴建鑫.风力机塔架的有限元建模及静动态特性分析[D].兰州：兰州理工大学，2011.

[16]赵世林，李德源，黄小华.风力机塔架在偏心载荷作用下的屈曲分析[J].太阳能学报，2010，31(7)：901-906.

[17]王印军，任勇生，孙丙磊，等.基于Ansys的垂直轴风力机塔架的力学分析及结构优化[J].山东科技大学学报，2011，30(5)：96-102.

[18]陆萍，秦惠芳，栾芝云.基于有限元法的风力机塔架结构动态分析[J].机械工程学报，2002，38(9)：127-130.

[19]刘雄，李钢强，陈严，等.水平轴风力机筒型塔架动态响应分析[J].太阳能学报，2010，31(4)：412-417.

[20]李源霜，李汶柏，张文明.大型椭圆振动筛空心裂纹转轴非线性振动特性分析[J].噪声与振动控制，2016，36（2）：46-51.

Analysis of the Influence of Sectional Structure on Vibration Characteristics of Wind Turbine Towers

CHENG You-liang,XUE Zhan-pu,QU Jiang-man,JIANG Yan
(School of Energy Power and Mechanical Engineering,North China Electric Power University, Baoding 071003,Hebei China)

The instability problem of the wind power towers induced by the sectional structure is studied.The rigid finite element method is used to establish the three-dimensional dynamic model of the sectional structure.The first five nonzero modals are extracted.The modal characteristics of the inner and outer flanges of the joints of the tower are studied under the turbulent conditions.The results show that the vibration displacements of the outer flange are all smaller than those of the inner flange.The magnitudes of vibration variation are small,so the resonance is unlikely to occur.The first order vibration of the outer flange plays a dominant role in nonlinear torsional deformation.The results provide a reference for the towers to avoid the resonance in the operation process.

vibration and wave;tower;sectional structure;vibration spectrum;torsional deformation

TK83

：A

：10.3969/j.issn.1006-1355.2017.03.007

1006-1355(2017)03-0037-05

2016-11-11

国家自然科学基金重点基金（11232012）；中央高校基本科研业务费专项资金项目（2016XS107）

程友良（1963－），男，博士，教授，博士生导师，主要研究方向为流体动力学理论及其应用、流体设备与节能、可再生能源理论及其应用、清洁能源利用技术与设备。

薛占璞（1983－)，博士研究生，专业为流体机械及工程，研究方向为清洁能源利用技术与设备。E-mail:shenghuo166@163.com