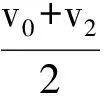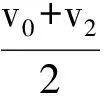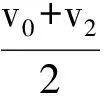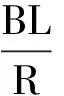例谈物理解题中似是而非的“平均值”

彭立君

(湖南省岳阳市第一中学，湖南 岳阳 414000)



例谈物理解题中似是而非的“平均值”

彭立君

(湖南省岳阳市第一中学，湖南 岳阳 414000)

本文通过解析两例采用平均值求解物理问题的过程,分析说明平均值求解问题的非一般性,当命题中的物理量处于变化状态时应采用微元分析，化变化量为不变量进行处理求解．

平均值； 均匀变化； 非一般性； 微元分析

当量值处于变化状态时,“平均值”是一种习惯的思维方式．当物理量处于均匀变化时,采用平均值处理问题也是物理解题中的一种常用方法．同样,命题者在命题时也往往在问题情景中设置均匀变化的物理量,促成解题时能够使用平均值处理．但是平均值求解并非十分严谨的科学方法,有时简单采用平均值处理可能会得到正确的答案,却不一定正确理解了物理情景,有时不经深思采用平均值进行问题的求解,则会造成问题的错解．下面,从两例问题来思考如何正确看待物理解题中的“平均值”．

1 “平均值”带来的解题失误

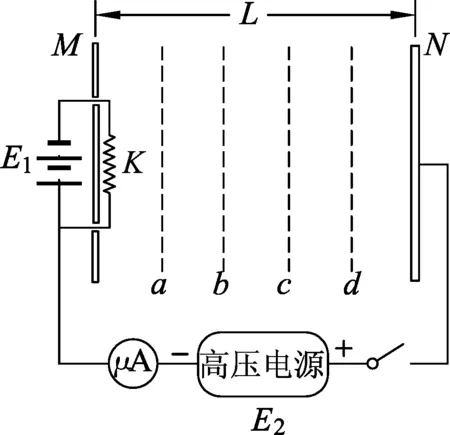
图1

例1.当金属的温度升高到一定程度时就会向四周发射电子,这种电子叫热电子,通常情况下,热电子的初始速度可以忽略不计．如图1所示,相距为L的两块平行金属板M、N接在输出电压恒为U的高压电源E2上,M、N之间的电场近似为匀强电场,a、b、c、d是匀强电场中4个均匀分布的等势面,K是与M板距离很近的灯丝,电源E1给K加热从而产生热电子．电源接通后,电流表的示数稳定为I,已知电子的质量为m、电荷量为e．求:

(1) 电子达到N板瞬间的速度;

(2) 电子从灯丝K出发达到N板所经历的时间;

(3) 电路稳定的某时刻,M、N之间运动的热电子的总动能．

本例题流转于网络、复习资料,甚至出现在大型考试中,无论是网络、复习资料还是考试中的参考答案一律采用平均值求解,恰恰本例虽是一种均匀变化，却不能采用平均值求解．

参考答案(第3问为典型错解):

(1) 电场中加速,由动能定理得

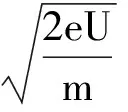
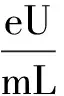
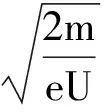
有没有更让人信服的方法求解呢?

图2

不妨作出t0时间内的带电粒子的v-t图像,如图2所示．设t0为带电粒子在电场中运动的时间,则v0为带电粒子到达右极板时的速度．同样也可以把图像看作是极板间所有粒子速度随时间的分布．由于电流稳定为I,在相等时间间隔内通过截面的电荷量相等,故图中取相等的时间间隔分析,其对应的电荷数相等．

设板间电荷总量为Q,则Q=It．

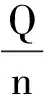
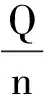
板间粒子总动能为

Ek总=∑Eki，

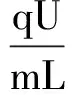
本例也可以直接从电场力做功等于动能的增量的角度来处理．

设板间电荷总量为Q,把电荷量按时间顺序均分为n等份，第n等份恰好到达N板,有

则第i等份到达的位置距离M板为

由动能定理知,第i等份电荷量所具有的动能为

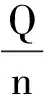
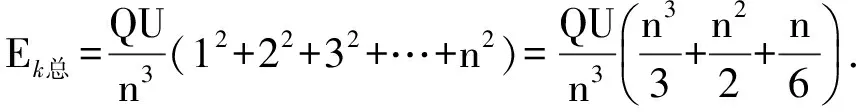
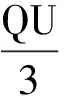
2 “平均值”似是而非的巧合

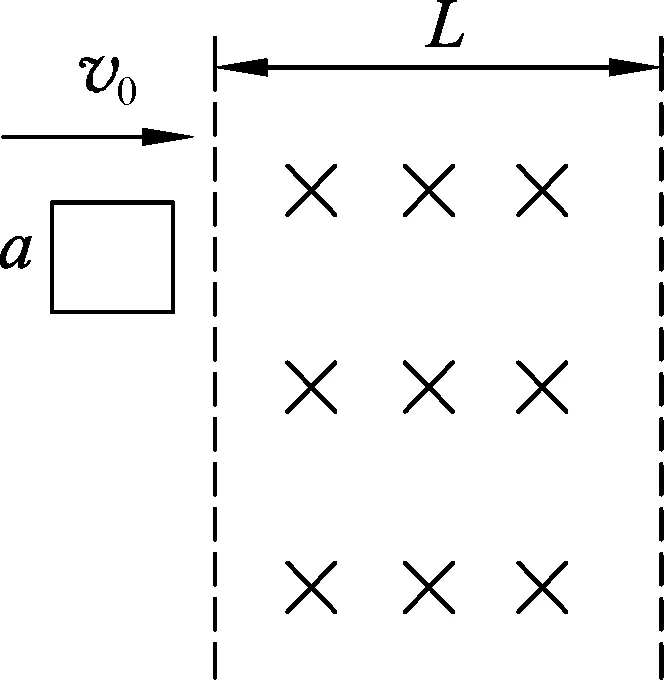
图3

例2.一有界匀强磁场区域的宽度为L,磁场方向竖直向下,在光滑的水平面上,一个边长为a(a

本例题也是常见于各种复习资料、网络中,看似一种不均匀变化,但又似乎能用平均值进行处理．最简单的想法,当然是相加除2．这是没有情景思考的一个想法,也巧合了本题的答案．

本题常采用动量定理求解．

对线框进入磁场过程分析,由动量定理可知

对线框穿出磁场过程分析,由动量定理可知

任取很短的一段时间Δti分析,由于时间很短电流可以看作不变量．

两边同乘以Δti，得

则这段时间内流过导线截面得电荷量为

由此可知

从以上两例的解析过程可知,“平均值”未经严谨的推理验证,并不能只根据想象就可以采用,它不是一种十分严谨的科学方法,是一种经验后的非一般性处理问题方法．当处理物理量发生变化的问题时,若未经严谨的逻辑推理,不应该采用“平均值”的方式处理,应采用微元分析把变量转换为不变量进行问题的分析．

本文系湖南省教育规划课题“数学模型在中学物理教学中的建构与应用研究”(批准号： XJK014CZXX077)的阶段性成果.

2017-02-12)