主瓣可控的鲁棒自适应波束形成算法*
武炳阳,马彦恒
(军械工程学院,河北 石家庄 050000)
主瓣可控的鲁棒自适应波束形成算法*
武炳阳,马彦恒
(军械工程学院,河北 石家庄 050000)
自适应波束形成技术能够有效地接收目标信号并抑制干扰,提高阵列输出的信干比。但传统自适应算法无法控制波束形状,为了形成固定主瓣宽度的波束,通过定义权重函数将波束形成问题转化为加权方向图综合问题,对协方差矩阵修正以提高算法鲁棒性,并用迭代FFT方法解决得到的表达式。通过仿真分析,该自适应波束器能够很好的控制主瓣宽度,并在干扰方向上形成零陷。
自适应波束形成;主瓣宽度;鲁棒性;循环FFT;空域滤波;协方差矩阵修正
0 引言
自适应波束形成是阵列信号处理中一个重要的研究方向。在给定优化准则的情况下,自适应天线阵列能够根据接收信号的变化自动调整权值,将方向图主瓣指向目标信号方向,同时在干扰方向形成零陷[1-2]。
传统的自适应波束形成算法在信号方向形成的主瓣较窄,且无法对其宽度进行准确的控制,在波束扫描中无法保证空间的覆盖。此外,当目标方向估计或目标信号阵列流形存在误差时,将会导致算法性能降低或失效。为了解决这些问题,可以产生一个相对较宽的平顶主瓣防止目标逃出主瓣角度并保证空间覆盖[3]。文献[4]提出基于二乘锥规划(SOCP)方法对波形进行约束,该方法在快拍数较小及模型存在误差时性能降低,并且需设定旁瓣电平值。文献[5]提出通过设计一个平顶的阵列响应函数进行约束,该方法需要较高的角度采样数,导致算法运算量极大。
本文提出一种基于循环FFT的鲁棒自适应波束形成算法,该方法可在低快拍条件下同时约束主瓣宽度、波纹大小和旁瓣电平,并提高了波束形成器的鲁棒性。通过仿真验证算法有效。
1 数学模型
1.1 自适应波束形成器信号模型
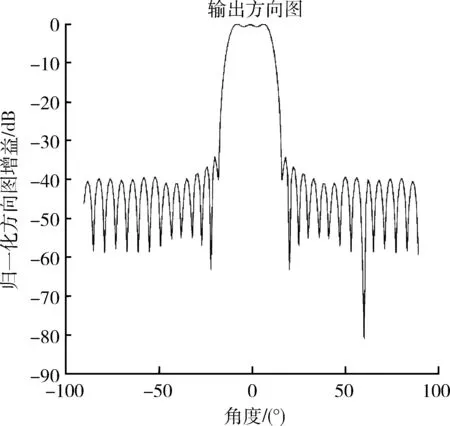
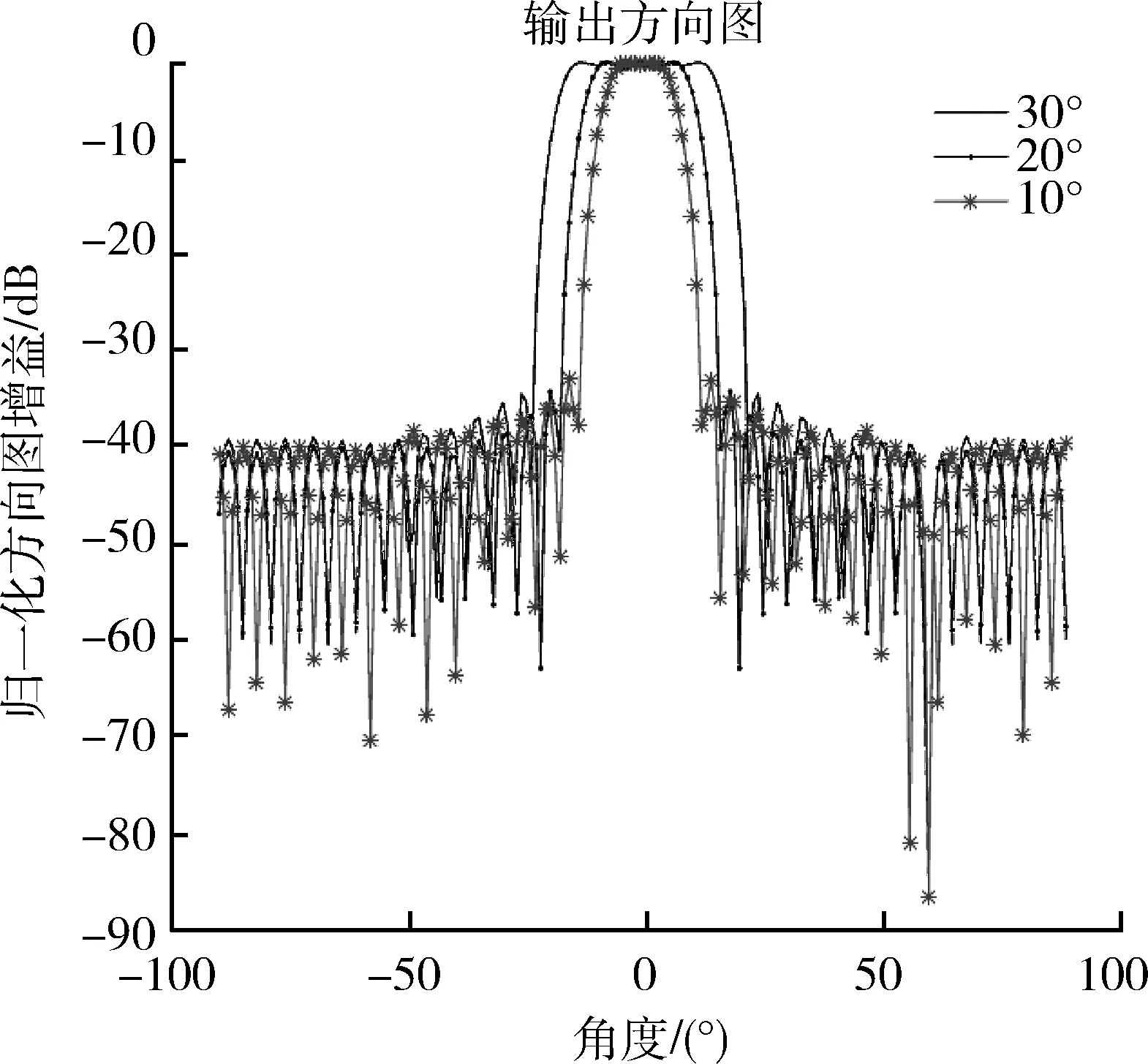
考虑一个N元均匀线阵,各个阵元均为全向阵元且间距为d,有一个远场窄带期望信号从θ0方向入射,M个远场干扰信号分别从θi(i=1,2,…,M)入射到阵列,且满足M+1 (1) 波束形成器输出为 (2) 式中:w=(w1,w2,…,wN)T为阵列加权矢量。 阵列输出总功率为 (3) 1.2 主瓣宽度可控的鲁棒自适应波束形成算法 为了对主瓣进行有效控制,本文将波束形成问题转换为一个加权方向图的综合问题,定义一个权重函数[6-7],如下: (4) (5) (6) (6) 循环直至得到目标方向图或达到最大循环次数。 1.3 信号协方差矩阵修正 将信号协方差矩阵Rx进行特征值分解[14]为 (7) 式中:λ0为期望信号对应的特征值,λi(i=1,2,…,M)为干扰信号对应特征值,λi(i=M+1,M+2,…,N-1)为噪声对应的小特征值;ui为λi对应的特征向量。由于Rx为Hermitian阵,所有特征值全部为实数且特征向量相互正交。用矩阵的形式表示式(7)得 (8) 式中:Ui,Un分别为Rx对应的干扰子空间和噪声子空间;Λi=diag{λ1,λ2,…,λM};Λi=diag{λM+1,λM+2,…,λN-1}。 在实际应用中,求解Rx采用SMI算法实现,该算法利用L次快拍数据估计得到Rx[15]。 (9) 但受快拍数有限的限制,噪声子空间的小特征值由于存在估计误差而产生发散,当快拍数L<2N时,发散加剧,导致副瓣升高、零陷变浅。 本文通过信号协方差矩阵Rx与单位阵E的凸线性组合来估计协方差矩阵为 (10) 式中:β为修正指数,且β∈[0,1]。 当β=1时,Rx干扰子空间与噪声子空间经修正后不变,此时在低快拍情况下仍然会出现小特征值发散。 当β=0时,Rx干扰子空间与噪声子空间经修正后相同为1,失去了对干扰的抑制能力。 当0<β<1时,Rx经过修正,干扰子空间与噪声子空间之间的比值减小,小特征值发散情况得以改善,波束形成器鲁棒性得以增强。在强干扰的情况下,β需要选取较大值进行抑制;在弱干扰的情况下,β需要选取较小值以加快波束形成器收敛速度。 综上,该修正方法可以抑制小特征值的扩散,增强算法鲁棒性。 下面通过仿真对算法性能进行验证。 接收阵列为一均匀线阵,阵元个数N=30,阵元且间距为半波长。假设期望信号入射角度范围为[-10°,10°],干扰信号入射方向为60°,信号信干比(SJR)为-20 dB,快拍数10次,根据SJR取值,仿真中修正指数β取0.5。图1给出本文算法输出的方向图。 图1 方向图Fig.1 Array pattern 从图1中可以看出,主瓣宽度约为20°,顶部平坦;旁瓣区域为[-90°,-14°]∪[14°,90°],方向图形状与设定条件相符。在干扰角度60°方向上,有-80 dB的零陷,能够有效地抑制干扰。 下面设定不同的主瓣宽度,设置平顶区域宽度分别为10°,20°,30°,干扰信号入射方向为60°,信号信干比(SJR)为-20 dB,快拍数10次,β=0.5。如图2所示,给出了不同主瓣宽度设置下的方向图。 图2 不同主瓣宽度设置下方向图Fig.2 Array pattern under different width of the main lobe 由图2可以看出,宽的主瓣可以提高波束形成器对模型误差的稳健性,但会导致零陷变浅,降低对干扰的抑制能力。因此在实际应用中,要根据空间覆盖率等指标需求,选取合适的主瓣宽度,以尽可能提高阵列输出信号的信干比。 本文提出一种主瓣可控的自适应波束形成算法,该算法在对信号协方差矩阵进行修正的基础上,将自适应波束形成问题转会化为一个加权方向图综合问题,使用迭代FFT算法产生平顶方向图。通过仿真实验验证了算法的有效性。 [1] STOICA P,LI J,ZHU X,et al.On Using a Priori Knowledge in Space-Time Adaptive Processing[J].IEEE Transactions on Signal Processing,2008,56(6):2598-2602. [2] 程乃平,倪淑燕.改进的特征空间波束形成算法[J].通信学报,2010,31(8):32-36. CHENG Nai-ping,NI Shu-yan.Modified Eigenspace-Based Beam-Forming Algorithm[J].Journal on Communication,2010,31(8):32-36. [3] 刘聪峰,廖桂生.最差性能最优的稳健波束形成算法[J].西安电子科技大学学报,2010,37(1):1-8. LIU Cong-feng,LIAO Gui-sheng.Robust Beam-Forming Algorithm with Worst Performance[J].Journal of Xidian University,2010,37(1):1-8. [4] JING L,GERSHMAN A B,ZHI-Quan L,et al.Adaptive Beam-Forming with Side-Lobe Control:A Second-Order Cone Programming Approach[J].IEEE Signal Processing Letters,2003,10(11):331-334. [5] YU Z,SER W,Meng Hwa E,et al.Robust Adaptive Beamformers Based on Worst-Case Optimization and Constraints on Magnitude Response[J].IEEE Transaction on Signal Processing Letters,2009,57(7):2615-2628.[6] 阳凯.阵列方向图综合与自适应波束形成技术研究[D].成都:电子科技大学,2013. YANG Kai.Research on Array Pattern Synthesis and Adaptive Beam-Forming Technologies [D].Chengdu:University of Electronic Engineering,2013. [7] 吴梦,刘宏伟,王旭.一种循环迭代的 MIMO 雷达发射方向图设计方法[J].电子与信息学 报,2015,37(3):322-327. WU Meng,LIU Hong-wei,WANG Xu.A Cyclic Iterative Method for MIMO Radar Transmit Beam-Pattern Design [J].Journal of Electronic & Information Technology,2015,37(2):322-327. [8] 李洪涛,贺亚鹏,朱晓华,等.一种低快拍情况下稳健的波束形成算法[J].信号处理,2011,27(6):809-912. LI Hong-tao,HE Ya-peng,ZHU Xiao-hua,et al.A Robust Beam-Forming Algorithm in the Situation of Limited Snapshots[J].Signal Processing,2011,27(6):809-912.[9] 张小飞,汪飞,陈伟华.阵列信号处理的理论与应用[M].北京:国防工业出版社,2013. ZHANG Xiao-fei,WANG Fei,CHENG Wei-hua.Theory and Application of Array Signal Processing [M].Beijing:National Defence Industry Press,2013. [10] 王文涛,张剑云,曹磊,等.FRFT应用于雷达抗主瓣压制干扰技术研究[J].现代防御技术,2011,39(1):125-128. WANG Wen-tao,ZHANG Jian-yun,CAO Lei,et al.Study on FRFT Application in Radar Anti-Jamming Technology [J].Modern Defence Technology,2011,39(1):125-128. [11] 王强,张永顺,司文涛.多干扰源环境下多基地雷达主瓣干扰抑制方法[J].现代防御技术,2015,43(3):35-48. WANG Qiang,ZHANG Yong-shun,SI Wen-tao.Main-Lobe Jamming Suppression Method in the Presence of Many Disturbance Sources[J].Modern Defence Technology,2015,43(3):35-48. [12] 洪振清,张剑云.基于二阶锥规划的MIMO雷达稳健自适应波束形成[J].现代防御技术,2012,40(3):137-143. HONG Zhen-qing,ZHANG Jian-yun.Robust Adaptive Beam-Forming Based on SCOP for MIMO Radar[J].Modern Defence Technology,2012,40(3):137-143. [13] 张德平,王超,袁乃昌.基于DDS阵列的发射数字波束形成系统设计[J].现代防御技术,2011,39(1):125-128. ZHANG De-ping,WANG Chao,YUAN Nai-chang.Design of Transmit Digital Beam-Forming System Based on DDS Array[J].Modern Defence Technology,2011,39(1):125-128. [14] GU Y J,LESHEM A.Robust Adaptive Beam-Forming Based in Interference Covariance Matrix Reconstruction and Steering Vector Estimation[J].IEEE Transactions on Signal Processing,2012,60(7):3881-3885. [15] 张珂,张剑云.单通道相控阵雷达及类波束形成技术[J].现代防御技术,2011,39(5):102-107. ZHANG Ke,ZHANG Jian-yun.Switch Antenna Phased Array Radar and Beam-Forming-Like Technology [J].Modern Defence Technology,2011,39(5):102-107. Robust Adaptive Beam-Forming Algorithm with Controllable Main-Lobe WU Bing-yang,MA Yan-heng (Ordnance Engineering College,Hebei Shijiazhuang 050000,China) Adaptive Beam-forming technology can effectively improve the SINR of array by receiving the desired signal and rejecting the interference, while traditional adaptive algorithms can not control the beam shape.In order to form a fixed width of the main-lobe, beam-forming problem is transformed into a weighted pattern synthesis problemby defining the weight function. The modified covariance matrix improves the robustness of the algorithm, and iterative FFT method is used to solve the resulting expression. The simulation results show the proposed method can control the width of the main-lobe and form a null in the direction of interference. adaptive beam forming;main-lobe width;robustness;circular FFT;spatial filtering;covariance matrix correction 2016-07-09; 2016-08-30 武炳阳(1992-),男,河北石家庄人。硕士生,主要从事多基地雷达信号处理研究。 通信地址:100080 北京海淀区马连洼街道东北旺路103号院 E-mail:wby1331@163.com 10.3969/j.issn.1009-086x.2017.03.021 TN959.6;TP301.6;TP391.9 A 1009-086X(2017)-03-0129-04


2 数值仿真
3 结束语

