生活中的几何
文 /韩丽华
智慧数学
生活中的几何
文 /韩丽华

责任编辑:王二喜
数学来源于生活,又服务于生活,学习数学的目的是为了运用数学知识来解决实际问题.在中考中,生活中的几何问题越来越受到命题者的青睐.
一、生活中的几何原理
例 1 (2016年永州卷)对下列生活现象的解释,其数学原理运用错误的是( )
A.把弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理.
B.木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中,垂线段最短”的原理.
C.将自行车的车架设计为三角形形状是运用了“三角形稳定性”的原理.
D.将车轮设计为圆形是运用了“圆的旋转对称性”的原理.
解析:任选两个点就能画出一条笔直的墨线是运用了“两点确定一条直线”的原理,B不正确.其他各选项正确.选B.
温馨小提示:用数学原理解释生活中的现象,熟悉常见的几何定理是解题的关键.
二、刀片上的角度
例 2 (2016年湖州卷)图1是我们常用的折叠式小刀,图2中刀柄外形是一个矩形挖去一个小半圆,其中刀片的两条边沿线可看成两条平行的线段,转动刀片时会形成∠1与∠2,则∠1与∠2的和是______度.

图1

图2
解析:如图2,AB椅CD,蚁AEC=90°.
所以∠1+∠2=∠AEF+蚁CEF=蚁AEC=90°.填90.
温馨小提示:利用平行线和矩形的性质,解决了将刀片转动时角度的计算问题.
三、足球射门的角度
例 3 (2016年金华卷)足球射门,不考虑其他因素,仅考虑射门点到球门AB的张角大小时,张角越大,射门越好.在图3的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射门点在( )
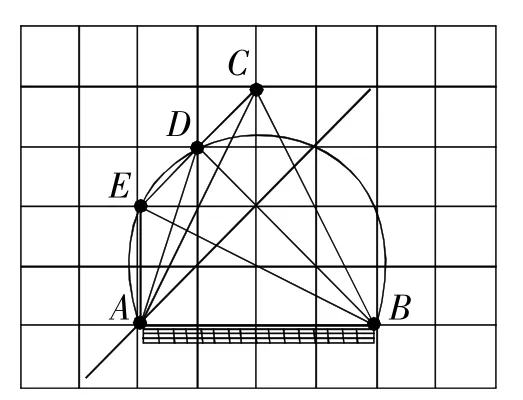
图3
A.点C. B.点D或点E.
C. 线段DE(异于端点)上一点. D. 线段CD(异于端点)上一点.
解析:连接EB,AD,DB,AC,CB,作过点A,B,D的圆,可以确定点E在圆上,点C在圆外,根据圆周角及圆外角的性质可以得到蚁AEB=蚁ADB>蚁ACB,所以最好的射门点是线段DE(异于端点)上一点.选C.
温馨小提示:构造辅助圆,根据圆周角、圆内角及圆外角的性质确定各张角的大小,进而得出结论.
四、地毯的面积
例 4 (2016年金华卷)一楼梯如图4所示,BC是铅垂线,CA是水平线,BA 与CA 的夹角为兹.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )

图4

温馨小提示:利用平移思想,将地毯的长转化为直角三角形两条直角边的和,就容易求面积.
五、求标语的长度

图5
例 5 (2016年宜昌卷)杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下:如图5,ABOHCD,相邻两平行线间的距离相等,AC,BD相交于O,ODCD,垂足为D,已知AB=20米.求标语CD的长度.

∵ 相邻两平行线间的距离相等,∴BO=DO,

温馨小提示:将实际问题转化为全等三角形的问题是解题的关键.
六、求行走的路程
例 6 (2016年十堰卷)如图6,小华从点A 出发,沿直线走10米后左转24°,再沿直线走10米,又向左转24°,一直这样走,当他第一次回到出发地A点时,一共走的路程是( )

图6
A.140米. B.150米. C.60米. D.240米.
解析:正多边形的外角和是360°,每次左转24°,所以360÷24=15,走的路程是一个边长为10米的正十五边形的周长,一共走了150米. 选B.
温馨小提示:本题把正多边形外角的计算与路程结合在一起,考查外角和的应用.
七、破碎的玻璃片
例 7 (2016年绍兴卷)小敏不慎将一块平行四边形玻璃打碎成如图7的四块,为了能在商店配到一块相同形状的玻璃,他带了两块碎玻璃,其编号应该是( )

图7
A.①② B.①④ C.③④D.②③
解析:只有②③两块角的两边互相平行,它们延长线的交点就是平行四边形的顶点.选D.
温馨小提示:要确定平行四边形,只需确定四个顶点.
八、求阁楼的高度

图8
例 8 (2016年陕西卷)小亮、小芳等同学想测量“望月阁”的高度,因观测点与“望月阁”底部间的距离不易测得,于是他们用平面镜进行测量.方法如下:如图8,在直线BM上平放一平面镜,在镜面上做了一个标记点C,镜子不动,小亮看着镜面上的标记走动,走到点D时,看到“望月阁”顶端点A 在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地 面的高度ED=1.5米 ,CD=2米.然后 ,在阳光 下,他们用测影长的方法进行了第二次测量. 方法如下:小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮的影长FH=2.5米,身高FG=1.65米.

解得AB=99.
答:“望月阁”的高AB为99米.
温馨小提示:要熟练掌握平行投影的性质和光线的入射角等于反射角的特征.
九、求物体上升高度
例 9 (2016年兰州卷)如图9,用—个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )

图9
A.仔cm. B.2仔cm. C.3仔cm. D.5仔cm.
解析:当滑轮上一点P旋转了108°时,重物上升的距离就是点P旋转的弧长
温馨小提示:将物体上升高度转化为弧长是解题的关键.
十、求扇形的面积
例 10 (2016年青岛卷)如图10,一折叠纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB 长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )

图10

解析:∵AB=25,BD=15,∴AD=25-15=10,



温馨小提示:扇环的面积等于两个扇形面积之差.

