传统方法解盈亏和鸡兔同笼类问题的局限性

☉重庆独立学者 熊 明

☉四川广安前锋区桂兴镇初级中学 熊 鉴

传统方法解盈亏和鸡兔同笼类问题的局限性

☉重庆独立学者 熊 明

☉四川广安前锋区桂兴镇初级中学 熊 鉴

盈亏问题和鸡兔同笼问题在我国古代用算术法求解，现今在小学也是用算术法求解，而在初中用方程法求解.但对于一些稍微复杂点的盈亏问题和鸡兔同笼推广问题，我们发现中国古代方法和传统的方程方法都不能得到这些问题的全部解.为此我们分别引入参变量的方程和不定方程组以弥补中国古代方法和传统方法在解决盈亏问题和鸡兔同笼类问题方面的缺陷和不足.在此与广大数学同仁交流和相互学习.

一、引入参变量解决某些盈亏问题的全部解

在代数和方程没有出现之前，古代中国人把“盈亏问题”划分为5类问题，对每类问题用相应的公式求解，这在当时领先世界.但当代数和一次方程的理论和方法完善后，解决这类问题变得非常简单，用一元方程或二元方程组便可解决.但某些盈亏问题存在多个解，仅仅靠公式法、一元方程法或二元方程组并不能得到全部解，而引入参数用不定方程可弥补这一缺陷和不足.尽管我们在2004年已经对盈亏问题传统解法做出过纠正，但现今网络上和某些辅导书上的求解方法仍然没有纠正过来.

例1 快乐幼儿园大班和小班的小朋友共43人，如果大班每人给7块糖，小班每人给5块糖，就多余15块糖；如果大班每人给10块糖，小班每人给7块糖，就有13位小朋友分不到糖.问：小班和大班各有多少个小朋友？（1998年2月27日香港小学数学精英选拔赛）

某些辅导书和网络上百度文库给出的解法：大班每人多发10-7=3（块），小班每人多发7-5=2（块），就需要多15+13×7=106（块）.因此小班人数是：（43×3-106）÷（3-2）=23，大班人数是：43-23=20.

我们认为求解时有如下两方面的情况需要考虑：（1）本题并没有指出未分到糖的小朋友是小班还是大班；（2）当大班按照每人10块糖分时，若不足10块则不再继续分，这时糖块可能还有剩余；同理，当小班按照每人7块分时，若不足7块，这时糖块可能仍有剩余.于是下面我们引入参变量并分类讨论.

解：设小班小朋友x人，则大班小朋友43-x人.因此按第一种分糖法，糖块总数为7（43-x）+5x+15，即-2x+ 316.

对第二种分糖法，下面我们分两种情况分别讨论：

（1）若未分到糖的13位小朋友为大班的，则设m表示不足10的糖块数，于是按第二种分糖法，糖块总数为7x+ 10（43-x-13）+m，从而得到含参变量m的方程-2x+316= 7x+10（43-x-13）+m.

整理上述不定方程得到x=m-16，其中m是0到9的整数，此时x＜0，因此此方程无意义，不再继续讨论.

（2）若未分到糖的13位小朋友为小班的，则设n表示不足7的糖块数，于是按第二种分糖法，糖块总数为7（x-13）+10（43-x）+n，其中n是0到6的整数.进而得到方程-2x+316=7（x-13）+10（43-x）+n，整理此方程得到x=23+n，其中n是0到6的整数.从而得到此方程的七个解：

最后可求得小班和大班的小朋友分别为23、20，或24、19，或25、18，或26、17，或27、16，或28、15，或29、14，共七种情形.原方法仅得到这七种情形的第一种.

上述问题中，若不分别引入一个参数m、n，建立含参变量的方程，则不能够得到该问题的全部解.

我们可以举出类似于例1的多个例子（略），读者可参阅“对盈亏问题传统解法的质疑和纠正”一文［1］.

二、“鸡兔同笼类”问题存在多个解

古代中国人解决“鸡兔同笼”这类问题在世界数学史上也是非常有名的.比较简单的“鸡兔同笼类”问题，我们既可以用中国古代传统的假设法求解，也可以用初中的一元一次方程或二元一次方程组求解.但对于稍复杂的推广类问题，这两种方法的局限性和缺陷便表现出来了.

1.一道小升初入学试题及其原解答.

例2 甲1分钟能洗3个盘子或9个碗，乙1分钟能洗2个盘子或7个碗.甲、乙两人合作，20分钟洗了134个盘子和碗.问：甲、乙共洗了几个盘子几个碗？说明理由.

原解答：假设20分钟都洗盘子，则可洗（2+3）×20= 100（个），共少洗了134-100=34（个）.甲如果洗1分钟碗，数量就要多9-3=6（个）；乙如果洗1分钟碗，数量就要多7-2=5（个）.因为6×4+5×2=34，所以洗碗的个数是4×9+2× 7=50，盘子的个数是134-50=84.

2.对上述小升初试题的进一步探讨.

上述方法是用中国古代传统的假设法求解的，解答过程非常简洁，那么是否还有其他解的情形呢？

我们发现：若乙把20分钟的时间全用于洗盘子，则可洗盘子40个洗碗0个；在此期间，甲分别用分钟洗盘子和洗碗，则甲分别洗了×9=51（个）盘子和碗；于是甲、乙两人洗盘子的总个数和洗碗的总个数则分别为83、51（盘子和碗总数仍然是134）.于是我们发现此问题的答案并不唯一.

进一步地，是否还有其他解？若有，如何求出这个问题的全部解？显然，传统的假设法显得无能为力！这就是这个古代假设法解决鸡兔同笼类问题的缺陷和局限性

3.对小升初试题的改编详解和引申.

例2的改编：甲1分钟能洗3个盘子或9个碗，乙1分钟能洗2个盘子或7个碗.甲、乙两人在20分钟内洗了134个盘子和碗（盘子和碗的总数为134）.甲、乙各自洗了多少个盘子和多少个碗？各自洗盘子和洗碗的时间分别是多少？

解：设甲洗的盘子和碗分别为x1、x2个，乙洗的盘子和碗分别为y1、y2个.则可根据他们洗盘子或碗的时间，以及盘子和碗的总数，列出如下四元方程组：

其中x1、x2、y1、y2都是非负整数.

上述方程组只有三个方程，但却有四个未知数，我们把这类方程组称为不定方程组.下面我用代入消元法求解该不定方程组.

将④⑤都代入方程③，从而得如下二元不定方程：

我们通过代入消元法已经将方程组化为了二元不定方程⑥.方程⑥变形为：

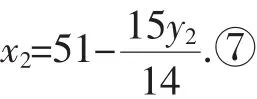
因为x2、y2都为非负整数，而且方程⑦中15和14互质，所以y2应该是14的整数倍，如果令方程⑦中的y2= 14k，再依次回代则可以得出x2、x1、y1关于k的表达式，从而可得到原不定方程组的一般解，如下：

因为根据此问题的实际情况，x1、x2、y1、y2都是非负整数，而当k取负整数或大于3的整数时，x2、y1便出现负数，不合题意，所以k只能取0、1、2、3这四个整数，从而得4个不同的解：

（x1，x2，y1，y2）=（43，51，40，0）、（48，36，36，14）、（53，21，32，28）、（58，6，28，42）.

由上可知：此方程组有且只有四个不同的解，即甲洗盘子和洗碗的个数及乙洗盘子和洗碗的情形有四种：（43，51，40，0），或（48，36，36，14），或（53，21，32，28），或（58，6，28，42）.

现在换一种代换方式，如果例2中方程①和②分别变形为x2=180-3x1和后，代入方程③，可得，整理后得

令y1=4m，则可得例2中原不定方程组一般解的另一种表达式：

其中m=7、8、9、10.两个表达式虽然形式上有差别，但可以验证两个表达式完全等价.

1.熊明.对盈亏问题传统解法的质疑和纠正［J］.基础教育（重庆），2004（7）.

2.基础教育考试评价中心.小学毕业升学真题详解·数学［M］.西安：西安出版社，2016.

3.熊明.在实数教学中渗透极限思想［J］.课程教育研究（中），2012（6）.