多带多重双向向量值小波包

张桂霞

(三门峡市教师进修学校，河南 三门峡 472000)



多带多重双向向量值小波包

张桂霞

(三门峡市教师进修学校，河南 三门峡 472000)

通过引进双向向量值多分辨分析与多带多重双向向量值小波包的概念.运用矩阵理论和时频分析方法，刻画了多带多重双向向量值小波包的性质，得到多带多重双向向量值小波包的正交公式，并且也得到了向量值函数空间L2(R,R3)的正交基.

双向向量值多分辨分析；面具函数；向量值正交小波；双向向量值小波包

1 问题的提出

小波分析(Wavelet Analysis)是近三十多年发展起来的一个数学分支，是应用数学和工程领域中一个飞速发展的新领域.向量值小波是一类广义的多小波[1]451-460.1996年，Xia和Suter[2]508-518首先引进了向量值小波的概念，研究了向量值正交小波的存在性及其构造方法，Fowler和Li利用离散的向量值正交小波变换研究海洋涡流现象[3]3018-3027. 2007年，杨守志教授引入了双向小波的概念[4]1908-1920，与传统意义上的小波相比，双向小波具有一般的情形，具有单小波和多小波都没有的某些性质，应用上也具有灵活性，譬如，人们可以利用双向小波变换得出心电图压缩算法[5]117-121.随着人们对小波分析研究的不断深入，双向小波成为了一个研究热点.与经典小波相比双向向量值小波有着明显的优势，在实施离散的多小波变换之前要预滤波，而实施离散的双向向量值小波变换则不需要进行预滤波，这样就大大地减少了工作量.所以，研究双向向量值小波是必要的.Luo L[6]10146-10157等引入了两尺度双向向量值正交小波的概念，陈清江等[7]662-673引入了多尺度双向向量值正交小波的概念，研究了它们的构造算法.双向向量值小波在向量值信号处理中应用广泛，然而，关于双向向量值小波的研究成果甚少.受文献[6,7]等的启发，本文研究刻画了多带多重双向向量值小波包的性质，得到多带多重双向向量值小波包的正交公式.

2 双向向量值多分辨分析

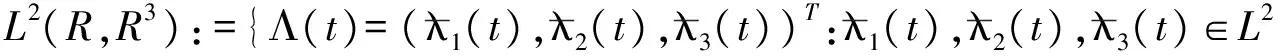
定义向量值函数Λ(t)∈L2(R,R3)的傅立叶变换为：

对任意的Λ(t)∈L2(R,R3)，‖Λ‖2表示向量值函数的范数，并且

对于两个向量值函数Λ(t),Γ(t)∈L2(R,R3)，定义它们的符号内积为：

其中“*”表示复共轭转置.如果向量值函数H(t)∈L2(R,R3)满足下面的双向加细方程

(1)

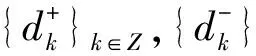
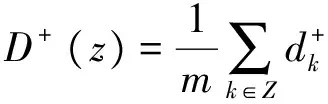
定义1 如果向量值加细函数H(t)∈L2(R,R3)满足(2)式，则称H(t)是正交的，

(2)

(3)

i) Yτ⊂Yτ+1，τ∈Z；

ii)Λ(t)∈Yτ⟺Λ(mt)∈Yτ+1, τ∈Z；

iii) ∩j∈ZYj={O}, ∪j∈ZYj在L2(R,R3)中稠密，其中O表示L2(R,R3)中的零向量；

iv) 双向向量值函数族{H(t-k),H(v-t):k,v∈Z}构成子空间Y0的一个Riesz基.

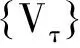
设Xτ是子空间Yτ在Yτ+1中的直交补空间，并且存在m-1个紧支撑的向量值函数Gα(t)∈L2(R,R3),α∈Ω:={1,2,…,m-1}，使得Gα(t)伸缩平移构成Xτ的Riesz基，即

(4)

由于Gα(t)伸缩平移构成Xτ的Riesz基，因此向量值函数Gα(t)应满足下面的加细方程

(5)

在(5)的两边做傅立叶变换可得：

(6)

定义2 设H(t)∈L2(R,R3)是双向向量值正交尺度函数，向量值函数Gα(t)满足(5)式.如果H(t)与Gα(t)满足以下条件，

(7)

则称Gα(t)是关于H(t)的双向向量值正交小波函数.

定理1 设Φ(t)是双向向量值正交尺度函数,Ψα(t)是对应于Φ(t)的双向正交向量值小波函数，则对于∀l∈Z，有以下结论成立：

证明：由于H(t)是双向向量值正交尺度函数，根据定义1，有：

即第(1)式成立，同理可以证明第(2)式至第(6)式也成立.

3 多带多重双向向量值小波包的性质

为了进一步细化频域带，将双向向量值小波的概念推广为双向向量值小波包.记：

定义3 称向量值函数族{Ψmr+μ(t):r∈Z+,μ∈Ω0}为对应于尺度函数Ψ0(t)的多带多重向量值小波包，其中Ω0:={0,1,2,…,m-1}，

(8)

在加细方程(8)的两边做傅立叶变换，得：

(9)

为了研究双向向量值小波包的性质，将(8)式改写为

(10)

记

(11)

因此，(11)式是关于双向向量值尺度函数Fmr+μ(t)的加细方程，并且它傅立叶变换为

(12)

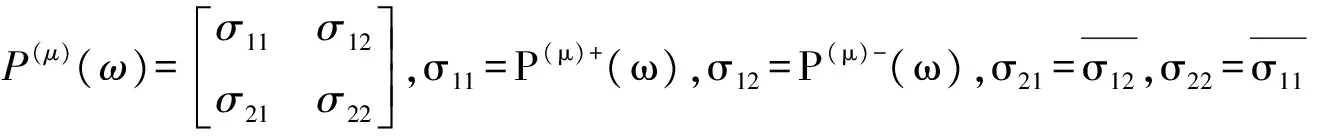
引理1[7]662-673若{Ψr(t):r∈Z+}是关于双向向量值正交尺度函数Ψ0(t)的小波包，则有

(13)

引理2[8]249-262如果{Ψr(t):r∈Z+}是关于Ψ0(t)的双向向量值小波包，则对m,r∈Z+,有

(14)

定理2 若{Ψr(t):r∈Z+}是关于Ψ0(t)的双向向量值小波包，则对∀α,β∈Z+,有

(15)

证明：根据矩阵理论，双正交关系式(15)等价于双正交关系式(16)

(16)

当α=β时，证明同定理2.现证α≠β的情形，令α>β，α=m[α/m]+ρ1，β=m[β/m]+μ1，情形1：如果[α/m]=[β/m]，那么ρ1≠μ1，

情形2：若[α/m]≠[β/m]，令[α/m]=m[[α/m]/m]+ρ2，[β/m]=m[[β/m]/m]+μ2，ρ2,μ2∈{0,1,…,m-1}.如果[[α/m]/m]=[[β/m]/m]，那么证明类似与情形1，现只证明[[α/m]/m]≠[[β/m]/m]的情况.再令[[α/m]/m]=m[[[α/m]/m]/m]+ρ3，[[β/m]/m]=m[[[β/m]/m]/m]+μ3,ρ3,μ3∈{0,1,…,m-1}，则，以同样的方式经有限步(记为θ步)运算后ρθ,μθ∈{0,1,…,m-1}，αθ,βθ∈{0,1,…,m-1}.若αθ=βθ，则ρθ≠μθ，由情形1知原命题成立.若αθ≠βθ，可以得到：

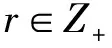
(17)

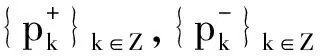
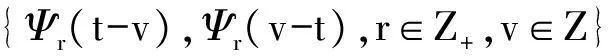
定理4 对于任意的n∈Z+，双向向量值函数族{Ψr(mjt-k),Ψr(k-mjt),r∈Εn,k∈Z}构成向量值函数空间L2(R,R3)的正交基．

证明：根据定理2，向量值函数族{Ψr(t-v),Ψr(v-t),r∈Εn,v∈Z}构成子空间DnX0的正交基,则对每一个j∈Z，{Ψr(mjt-v),Ψr(v-mjt),r∈Εn,v∈Z}构成子空间DjDnX0的正交基．所以，对任意的正整数n，则有

⊕表示子空间的正交和.因此，向量值函数族{Ψr(mjt-v),Ψr(v-mjt),r∈Εn,v∈Z}构成向量值函数空间L2(R,R3)的正交基．

[1]YangS，TangY，ChengZ.Constructionofcompactlysupportedorthogonalmultiwaveletwithscale=a[J].MathematicaNumericaSinica，2002，25(01).

[2]XiaXG，SuterBW.Vector-valuedwaveletsandvectorfilterbanks[J].IEEETransactionsonSignalProcessing，1996，44(03).

[3]FowlerJE，LiH.WaveletsTransformsforVvectorFieldsUsingOmnidretionallyBalancedMutli-wavelet[J].IEEETransactionsonSignalProcessing，2002，50(12).

[4]YangShouzhi，LiYoufa.Two-directionrefinablefunctiongsandtwo-directionwaveletswithdilationfactorm[J].AppliedMathematicsandComputation，2007，188(02).

[5] 费小英，王培康.基于双向小波变换的心电图压缩算法[J].航天医学与医学工程，2002，15(02).

[6]LuoL，LiW，LiQ.Astudyonorthogonaltwo-directionvector-valuedwaveletsandtwo-directionwaveletpackets[J].AppliedMathematics&Computation，2011，217(24).

[7] 陈清江，王晓凤，白 娜.多尺度双向向量值小波的构造与性质[J].应用数学，2015，28(03).

[8] 杨守志，郑贤伟.L2(Rn)上的半正交多小波框架[J].中国科学:数学，2014，44(03).

[责任编辑 梧桐雨]

Multiple Vector-Valued Two-direciton M-band Wavelet Packets

ZHANG Guixia

(SanmenxiaTeacherEducationSchool,Sanmenxia472000,China)

The notion for vector-valued two-direction multiresolution analysis and multiple vector-valued two-direction m-band wavelet packets are introduced. The properties for multiple vector-valued two-direction m-band wavelet packets are characterized by virtue of matrix theory and time-frequency analysis method. The orthogonal relationship formulae concerning the multiple vector-valued two-direction m-band wavelet packets are obtained. Moreover, orthogonal bases ofL2(R,R3) are constructed.

vector-valued two-direction multiresolution analysis; mask function；orthogonal vector-valued wavelets; multiple vector-valued two-direction m-band wavelet packets

2016-12-15

国家自然科学基金项目“低秩张量恢复及应用”(61403298)；陕西省自然科学基金项目“索伯列夫空间中小波框架的性质及其应用研究”(2015JM1024)

张桂霞(1965- )，女，河南三门峡人，三门峡市教师进修学校高级讲师,主要从事微分方程研究。

O174.2

A

1671-8127(2017)03-0076-05