几个数学建模案例在高等数学教学中的应用

康 卫，荆 科

（1.阜阳师范学院信息工程学院，安徽 阜阳 236041；2.阜阳师范学院数学与计算科学学院，安徽 阜阳236037）

几个数学建模案例在高等数学教学中的应用

康 卫1，荆 科2

（1.阜阳师范学院信息工程学院，安徽 阜阳 236041；2.阜阳师范学院数学与计算科学学院，安徽 阜阳236037）

本文主要研究了几个数学建模案例在高等数学教学中的应用，通过案例能够更好地理解高等数学中零点定理、微分方程的概念以及数学期望的知识点。进一步分析了将数学建模思想融入高等数学教学过程中的必要性，提升了学生学习高等数学的意识，进而培养学生利用数学思想去解决实际问题的能力。

高等数学；数学建模；教学案例

一、引 言

众所周知，高等数学的学习对很多理工科以及经管类专业的学生是至关重要的。其一，高等数学是大一新生进校后首先面临的一门重要的基础课程，而且高年级的很多课程甚至研究生阶段的部分课程都可以看成是它的延伸和应用。其二，学习高等数学能够增强学生的逻辑思维能力，还为分析和解决实际问题提供了必要的工具。因此高等数学这门课学习程度的好坏会对后继课程的学习和学生知识能力的培养产生影响的深远。 但是，现在的高等数学的教学模式仍然是以老师教、学生学为主，这样导致了很多学生不能灵活的运用数学理论知识来分析解决实际生活中的一些问题。 由于，数学建模这门课程提供了很多具体的案例来诠释如何将实际问题转化为数学问题，进而利用数学知识作为工具去解决这些实际问题。所以在高等数学的教学过程中老师应该适当的引入一些典型的数学建模案例，这样能够使学生更加深刻的理解高等数学课本中那些难以理解、枯燥乏味的数学定理和定义，进而促使学生对学习高等数学产生浓厚的兴趣。

我们知道由于几何学、物理学、天文学等研究领域的进展和突破，推动了高等数学的发展。从物体运动的三大定律到发现万有引力，从行星运动中切向加速度等于零的现象到极值问题的探讨研究，进一步到微分中值定理的形成，这些物理学中的现象都充满着无比深奥的数学建模思想，[1]从而推动了高等数学向前发展。除此之外，我们还可以通过对自然现象中许多数学关系的变化，发现他们之间的规律，建立各种各样的数学建模案例。 如果能够在高等数学的教学过程中去引入这样的数学建模案例，就可以增加老师和学生之间的互动性，丰富课堂教学的内容，开阔学生的眼界，激发学生学习兴趣，提升学生的数学素养。下面本文就引入三个具体的数学建模案例来诠释其在高等数学教学中的应用。

二、数学建模案例在高等数学教学中的应用

1.零点定理与椅子放平问题

高等数学中有很多重要的定理，学生学了但是不知道有什么作用。如果能够和实际问题相结合，往往能够让学生更容易理解，印象更为深刻，起到事半功倍的效果。下面我们引入数学模型[2]来解释高等数学中的零点定理。

例1：四条腿一样长的椅子可以在不平坦的地面上放稳吗？

乍一看，这是一个和数学毫无相关的问题，然而，我们如果能够把这个实际问题转化成数学模型，把它转化成为数学语言来表达，进而利用数学中的定理作为工具来解决这一问题，一定可以引起学生的兴趣。接下来，我们经过合理的简化假设把此问题转化为数学问题。

已知 f（θ），g（θ）是某闭区间上的连续函数，对任意的θ我们有f（θ）＊g（θ）＝0并且f（0）＞0，g（0）＝0，则证明至少存在一点θ0，使f（θ0）＝0，g（θ0）＝0.

证明：首先，将椅子旋转900（π／2），由于f（0）＞0，g（0）＝0，可以得到f（π／2）＝0，g（π／2）＞0，下一步，令h（θ）＝f（θ）－g（θ），则h（0）＞0和h（π／2）＜0.

又因为 f（θ），g（θ）都是连续函数，因此可以得到f（θ）也是一个连续函数。然后，利用数学中的零点定理，可以知道至少有一点θ0（0＜θ0＜π／2）使得h（θ0）＝0，最后，根据 f（θ0）＊g（θ0）＝0，可得 f（θ0）＝g（θ0）＝0.

2．乒乓球比赛胜负问题

通过这个数学建模案例可以更好地使学生理解概率中期望的数学含义。以达到增强学生的好奇心，活跃课堂气氛，开阔视野的效果。

例2.乒乓球是我们得的国球，中国队在这项运动中具有绝对的优势.现就乒乓球比赛的安排提出一个问题：假设韩国队和中国队比赛，赛制有两种，一种是双方各出3人，三场两胜制，一种是双方各出5人，五场三胜制，哪一种赛制对中国队更有利？

由于中国队在这项比赛中的优势，我们不妨设中国队每一位队员对韩国队员的胜率都为60%.根据前面的分析，下面我们只需比较两队的数学期望即可。

在五场三胜制中，中国队要取得胜利，获胜的场数有3、4、5三种结果.我们计算三种结果所对应的概率、应用二项式定律可知，恰好获得三场胜利对应的概率：恰好获得四场对应的概率五场全胜的概率：

因此随机变量X的数学期望：

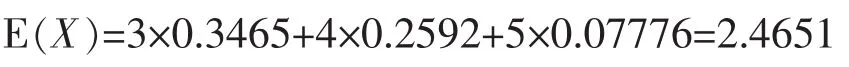
在三场两胜制中，中国队取得胜利，获胜的场数有2、3两种结果.胜两场对应的概率为：

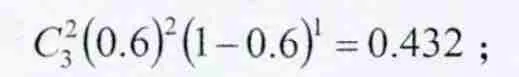
因此随机变量X的数学期望：

比较两个期望值，所以我们可以得出结论，五场三胜制对中国队更有利。

3．湖泊体积及平均水深的估算.

通过文献中的这一案例[3]，可以使学生对抽象的重积分程建立直观印象，还能使学生认识到重积分与实际联系比较密切的教学内容。

例3．椭球正弦曲面是许多湖泊的湖床形状的

被积函数和区域D的形状启示我们用变换

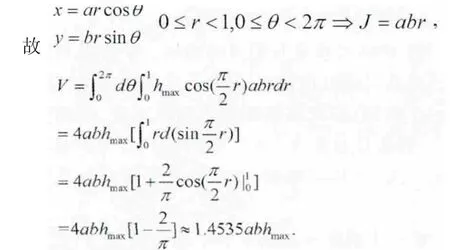
上述公式可估计湖水的体积。容易证明椭圆D的面积为πab，因而平均湖水深度为：

三、小结

通过以上的三个具体的数学建模案例，我们可以看出在高等数学的教学过程中融入数学建模的思想可以给学生直观上的感受，也可以引导学生自主学习，自主思考的能力，关键是还可以使得学生利用数学知识作为工具去解决实际的问题，培养了学生的推理、计算的能力。 另一方面，我们老师在高等数学授课过程中也应该引导学生参加大学生数学建模竞赛，以赛促教，让学生喜欢高等数学，热爱数学建模，让学生通过参加数学建模竞赛发挥他们的才智，享受数学建模的过程，享受学习高等数学的快乐。 总之，在高等数学教学过程中尽可能多的引入数学建模案例，达到事半功倍的效果，同时培养学生把高等数学知识作为强有力的工具来解决实际问题的能力，是我们高等数学老师追求的目标。

[1]张玉吉.数学建模在高等数学教学中的渗透[J].长春理工大学学报（高教版），2009,4（2）：147-148.

[2]姜启源，谢金星，叶俊.数学模型[M].北京：高等教育出版社，2011.

[3]梅顺治,刘富贵.高等数学方法与应用[M]，科学出版社，2000.

编辑：崔月华

On Application of Mathematics Models to the Process of Teaching Advanced Mathematics

KANG Wei1，JING Ke2
（1.School of Information Engineering,Fuyang Teachers College,Fuyang Anhui 236041；2.School of Mathematics and Computational Science,Fuyang Teachers College，Fuyang Anhui 236037）

In this paper，we analysis the application of several mathematical modeling cases in advanced mathematics.In order to understand Existence theorem of zero point,the concept of differential equations and mathematical expectation,some mathematical modeling cases was introduced.Then,we analysis the necessity of integrating mathematical modeling into the teaching of advanced mathematics,stimulates the students'interest,and cultivate students'ability to integrate theory with practice.

advanced mathematics；mathematics models；teaching cases

G642

A

2095-7327（2017）-01-0190-03

康卫（1985-），男，安徽利辛人，阜阳师范学院讲师，博士研究生，研究方向：数学建模、控制理论。

荆科（1983-），男，安徽颍上人，阜阳师范学院讲师，博士研究生，研究方向：数值逼近、统计计算。

安徽省教育厅自然科学研究重点项目（KJ2016A555），安徽省专业综合试点改革项目（2014zy138），安徽省教学团队项目（2015jxtd121），阜阳师范学院教研项目（2013JYXM48）,阜阳师范学院科研项目（2016FSKJ07）。