3正则的ID-因子临界图

梁彩霞

（肇庆学院 数学与统计学院，广东 肇庆 526061）

3正则的ID-因子临界图

梁彩霞

（肇庆学院 数学与统计学院，广东 肇庆 526061）

如果对于G中任意和 ||V(G)有相同奇偶性的独立集I,G-I有完美匹配,则称图G是ID-因子临界图，给出了3-正则的ID-因子临界图的刻画.

完美匹配;3-正则;独立集;ID-因子临界图

1 概述

文中未定义的术语和概念参见文献[1].本文涉及的图为有限、无向的简单图.令S为图G的顶点的子集，G-S的奇分支数记为o(G-S).设u是G中任一顶点，记意2点不相邻,则称I为独立集.若G的所有顶点的度都等于k,则称G为k-正则图.图G不包含K1,3为导出子图，称之为无爪图.对边集M⊆E(G),如果G的任意顶点至多与M中的1条边关联,则称M是G的匹配.称覆盖所有顶点的匹配为完美匹配.

因子理论一直是图论中的重要研究领域[2],对因子理论的研究最早可以追溯到1个世纪以前.1891年，Peterson[3]指出：2-边连通的3-正则图有1-因子，这被认为是现代因子理论研究的开始.1947年，Tutte[4]给出一个普通图G有1-因子的充要条件,该结论是因子理论中最基本的理论,奠定了因子理论的基础.1952年，Tutte[5]又给出图G有 f-因子的充要条件；1970年，Lovász[6]得到一个图G有(g,f)-因子的充要条件.从那时起，关于图的因子理论的结果不断涌现.如果对于G中任意顶点u,G-u有完美匹配(即1-因子)，则称G是因子临界图.在文献[7]中,原晋江把因子临界图的概念推广为独立集可削去的因子临界图.如果对于G中任意和 ||V(G)有相同奇偶性的独立集I,G-I有完美匹配，则称图G是独立集可消去的因子临界图(简称为ID-因子临界图).ID-因子临界图的研究成果可参见文献[8-12].本文刻画了3-正则的ID-因子临界图，进一步完善了图的因子理论.

2 主要结果与证明

引理1[4]若图G有完美匹配,当且仅当对任意的S⊆V(G),o(G-S)≤ ||S.

由图的正则性，在以下的讨论中G中顶点的个数为偶数.

定理1 无爪的3-正则ID-因子临界图只有图1中的G1,G2及G3.

证 易验证G1,G2及G3都是无爪的3-正则ID-因子临界图.设G是无爪的3-正则ID-因子临界图，下面证明G同构于G1,G2或G3.设u是G中任一顶点，由G是无爪图知1≤f(u)≤3.

情形1 f(u)=1.

在该情形下，2≤ ||N(2)(u)≤4.不失一般性，不妨设x1与x2相邻，由G的正则性知x3与N(2)(u)中的2个顶点，不妨设为y1与y2相邻，且由G无爪知y1与y2相邻.

当 ||N(2)(u)=2时，由G是3-正则的知xi(i=1,2)与且仅与y1和y2中之一相邻，yi(i=1,2)与且仅与x1和x2中之一相邻，此时G≅G1.

当 ||N(2)(u)=3时，不失一般性，设另有y3∈N(2)(u),且y3与x1相邻.若x2也与y3相邻，取I={ } x3,y3，则G-I含有奇分支，与引理1矛盾，从而x2与y3不相邻.不妨设x2与y2相邻，则有y1与y3必不相邻，否则图G含有以y3为中心的爪.从而I={ } y1,y3是G中的独立集,且G-I含有奇分支，矛盾.

当 ||N(2)(u)=4时,不失一般性，设另有y3,y4∈N(2)(u),且y3与x1相邻，y4与x2相邻.断言1 y3与y1和y2不相邻，y4与y1和y2不相邻.

若y3与y1相邻，则y3与y2也相邻，否则含爪.由G是3-正则的，有取含有奇分支,矛盾，从而有y3与y1不相邻，类似地有y3与y2不相邻，y4与y1,y2不相邻.

断言2 y3与y4不相邻.

假设y3与y4相邻，且y3与z∈N(3)(u)相邻.若y4与z相邻，取I={ } z,x3,G-I含有奇分支,矛盾；若y4与z不相邻，取

否则，设w∈N(4)(u),由断言2知是图G中的独立集，但G-I含有奇分支,矛盾.

当 |N(3)(u)|=6时，由G的正则性知与且仅与N(2)(u)中的1个顶点相邻.不妨设y1与z1相邻，取独立集则G-I含有奇分支,矛盾．

情形2 f(u)=2.

不失一般性，设x1,x2均与x3相邻.在这种情形下

情形3 f(u)=3.

显然，此时G≅K4=G3.

定理2 含爪的3-正则ID-因子临界图只有图2中的G4,G5,G6,G7,G8.

证 易验证图2中的Gi(i=4,5,6,7,8)是含爪的3-正则ID-因子临界图.设G是含爪3-正则ID-因子临界图，下证明G同构于图2中的Gi(i=4,5,6,7或8).不妨设G′是G中的1个爪,其中V(G′)={ } u,x1,x2,x3,u是该爪的中心.

由定理1和定理2显然有以下推论1.

推论1 3-正则的ID-因子临界图有且只有8个，见图1和图2.

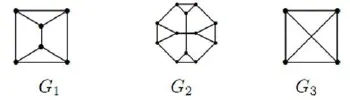
图1 无爪的3-正则ID-因子临界图

[1] BONDY JA,MURTY S R.Graph theory with applications[M].London:Macmillan Press Ltd,1976.

[2] 于青林,刘桂真.图的因子和匹配可扩性[M].北京：高等教育出版社,2010.

[3] PETERSEN J.Die theorie der regulären[J].AetaMath,1891,15:193-220.

[4] TUTTE W T.The factorizations of linear graphs[J].London Math Soc,1947,22:107-111.

[5] TUTTE W T.The factors of graphs[J].Can J Math,1952(4):314-328.

[6] LOVÁSZ.Subgraphs with prescribed valancies[J].J Comb Theory Ser B,1970(9):391-416.

[7] YUAN Jinjiang.Independent-set-deletable factor-critical power graphs[J].Acta Mathematica Scientia,2006,26B(4):577-584.

[8] LIU Yan.The degree conditions of ID-factor-critical graphs[J].SouthestAsian Bulletin of Mathematics,2003,27:641-648.

[9] LIANG Caixia,LIU Yan.The degree sum conditions of ID-factor-critical Graphs[J].Chinese Journal of Engineering Mathematics,2006,23:169-174.

[10] 马芳,刘岩.独立集可削去的因子临界图和无爪的独立集可削去因子临界图的度条件[J].华南师范大学学报(自然科学版),2008(2):29-33.

[11] MA Fang,LIU Yan.ID-factor-critical and claw-free graphs of diameter 2[J].Southeast Asian Bulletin of Math，2009,33:879-883.

[12] LIANG Caixia,LIU Yan.ID-factor-critical claw-free Graphs[J].Pacific Journal ofApplied Mathematics,2013,4(5):253-258.

3-Regular ID-Factor-Critical Graphs

LIANG Caixia

(School of Mathematics and Statistics,Zhaoqing University,Zhaoqing,Guangdong 526061,China)

:Gis ID-factor-critical if for every independent setIofGwhich has the same parity with ||V(G), G-Ihas a perfect matching.The 3-regular ID-factor-critical Graphs are characterized.

:perfect matching;3-regular;independent set;ID-factor-critical

O157.5

A

1009-8445（2017）02-0008-04

（责任编辑：陈 静）

2016-07-01

广东省自然科学基金资助项目（2014A030310277）；肇庆学院教学质量工程项目（80111323）

梁彩霞（1978-），女，广东茂名人，肇庆学院数学与统计学院讲师，硕士.