斜坡形非全周滑阀的特性研究

张友杰，倪受春

斜坡形非全周滑阀的特性研究

张友杰，倪受春

针对斜坡形非全周滑阀，推导出阀口的过流面积计算公式，并对过流面积的变化特点进行分析；利用流场仿真的方法得到了不同流动方向下的阀芯稳态液动力，结果表明油液在阀口内的流动方向不同，阀芯稳态液动力有明显差距。在流入方向，稳态液动力值很小，几乎可以忽略。

斜坡形非全周滑阀；过流面积；稳态液动力

非全周开口滑阀由于具有水力半径大、抗阻塞性能好、阀口面积梯度易调节、流量控制范围宽等优点[1-2], 因此在工程机械多路阀主控制阀芯等液压阀中得到了广泛应用[3]。

液压控制阀的流量控制特性本质上取决于其阀口过流面积和流量系数，节流槽滑阀阀口面积特性较传统滑阀丰富，但其计算要比传统滑阀复杂的多。冀宏等人在推导节流槽阀口过流面积上作了大量研究[4]，但由于节流槽形式的多样性，多数节流槽的阀口面积还未有现成的公式[5]，包括本文提出的斜坡形节流槽。

滑阀液动力除对操纵力有影响外，还对阀的动态响应特性有影响[6]。且近年来对于节流槽形式滑阀液动力的研究成果已经颠覆了传统的认识，如冀宏等[7]利用流场计算研究了非全周开口滑阀U型和V型节流槽稳态液动力,发现在特定的阀口开度范围内，液动力会使阀口趋于开大；方文敏[8]等通过试验测试和流场仿真相结合的方法,分析带U形节流槽滑阀的稳态液动力,结果表明不论是在单向流出流入情况还是在双向进出油情况下,带U形节流槽滑阀的稳态液动力会出现负值,使阀口趋于打开。

本文根据节流槽阀腔内的压力分布，确定了斜坡形非全周阀口过流面积的计算方法，并准确推导了该形式阀口过流面积的计算公式；利用CFD技术仿真得到了流体在流出和流入阀口时阀芯的稳态液动力。

1 阀口过流面积的计算方法和公式推导

1.1 阀口过流面积的计算方法

本文所研究的斜坡形阀口属于渐扩形节流槽，其典型特征为随阀口开度的变化截面逐渐变大，应用最小过流面来计算阀口面积[9]。

图1给出了斜坡形节流槽的结构简图及压力分布解析结果,可以看出:阀进出口压差集中分布在斜面A上，斜坡形节流槽的阀口面积A可按阀口开度处的截面A1在斜面A上的投影面积计算。

图1 斜坡形阀口过流面积

即斜坡形阀口过流面积：

(1)

式中：β为阀口坡角。

1.2 阀口过流面积公式推导

图2为斜坡形阀口过流面积计算简图，可以看到图1中的面积A1即为图2中A-A剖面图中空白部分的面积。

图2 斜坡形阀口过流面积计算简图

定义r=d/2，则阀口过流面积函数解析式为：

(2)

式中：x为阀口开度，β为阀口坡角，A为斜坡形阀口过流面积。

取d=20mm，给出了不同阀口坡角时阀口面积随阀口开度的变化规律，如图3所示，面积曲线线性度较好，整体曲线呈现凹型，说明随着阀口开度的增加其面积增益越大。

图3 阀口面积曲线

2 阀芯稳态液动力计算

2.1 稳态液动力的计算方法

计算阀芯的稳态液动力，目前有两种方法，一种是用传统的动量定理法，针对某一质点系的控制体，寻求动量变化与作用力之间的相互关系；另一种方法为通过CFD技术对壁面进行积分以得到流体对壁面的作用力。

2.1.1 动量定理法

用动量定理计算稳态液动力的公式：

(3)

式中：ρ为流体密度；q为流量，v2,v1分别是流体流入和流出控制体的速度，θ2,θ1分别是流体的入射角和出射角。

由于阀口射流角会随阀口开度的变化而变化[7]，用式(3)因此很难准确计算阀芯稳态液动力，只能定性判断液动力的方向和变化趋势。因此本文仅用动量定理法进行定性分析，而不再作为定量计算的依据。

2.1.2 基于CFD的壁面积分法

CFD技术可以得到阀腔内流场压力分布的数值解，对阀芯与流体的接触面积进行积分可以得到阀芯的液动力，求解公式可以表示为：

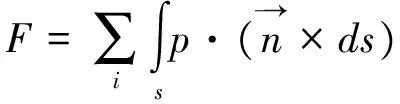
(4)

2.2 稳态液动力的仿真计算

2.2.1 几何模型

稳态液动力是指流体流入和流出控制体时由于动量的变化而对阀芯造成的附加作用力，可以分解为轴向分量和径向分量。由于节流槽一般对称布置，径向分量可以相互抵消，因此只需研究轴向作用力。为了研究方便，本文在建模时只取单节流槽作为研究对象。几何模型图4所示。

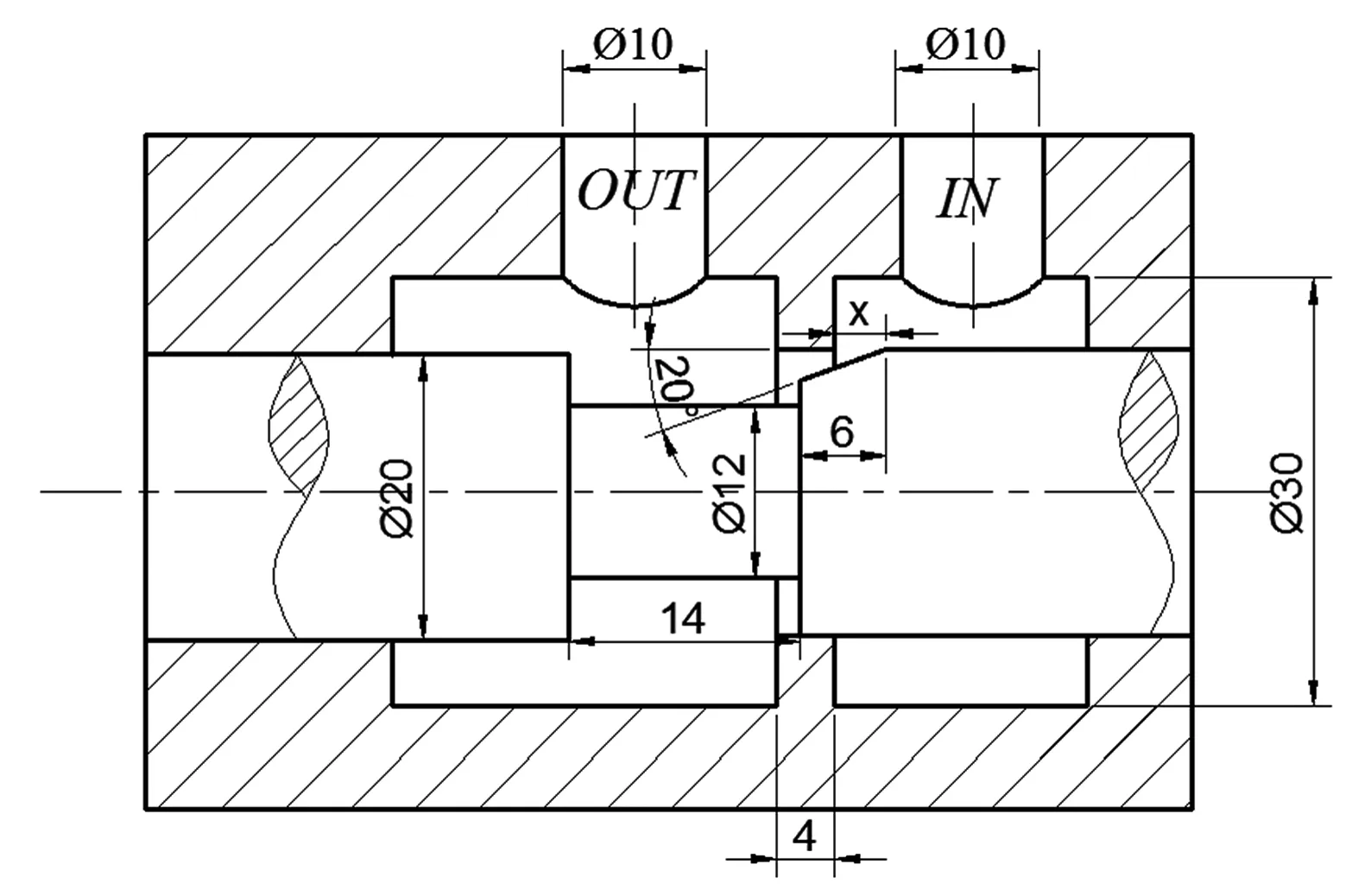
图4 几何模型

为了便于叙述，图4所示的IN→OUT的流动方向定义为流入方向，反之则为流出方向。

2.2.2 三维建模与网格划分

在Proe中进行三维建模并导入到ICEM中进行网格划分。采用非结构化网格，三维对称结构，在阀口区域进行局部细化。网格划分结果图5所示。

2.2.3 边界条件设置

利用fluent软件完成流场计算，采用恒压差边界条件，设置进口压力16Mpa，出口压力10Mpa；油液密度870kg/m3，动力粘度0.051pa·s；采用标准k-ε湍流模型，收敛准则为0.001。

2.2.4 稳态液动力计算结果

Fluent提供了物理量对于面的积分功能，在ICEM中标定阀芯的受力面，可以在Fluent中直接通过积分功能得到阀芯的稳态液动力。稳态液动力计算结果图6所示。

图5 计算网格

图6 稳态液动力曲线

2.2.5 计算结果分析

图6可以发现，流体在流入和流出阀口时稳态液动力差距很大。流出阀口时液动力为负值，方向使得阀口趋于关闭，随着阀口开度的增加液动力值变大；流出控制体时液动力值很小，但考虑到仿真计算时的误差，本文不对此时的液动力方向加以研究，仅对两者出现较大差距的原因进行分析。

图7为流体流入和流出阀口的速度矢量图，黑色粗线条包围区域为稳态液动力计算控制体。可以发现，流体按(a)方向流动，入射角几乎为90°，其轴向分量很小；流体按(b)方向流动，出射角依然存在很大的轴向分量。根据式(3)可以分析，流体在流入方向稳态液动力很小，流出方向液动力较大。

图7 速度矢量图

3 结语

推导了斜坡形非全周阀口的过流面积计算公式，并用流场仿真的方法分析阀芯的稳态液动力，得出以下结论：

(1)斜坡形非全周阀口过流面积线性度较好，且随着阀口开度的增加其面积增益越大；

(2)油液在阀口内的流动方向不同，阀芯稳态液动力有明显差距。在流入方向，稳态液动力值很小，几乎可以忽略。

[1] 林建亚, 何存兴.液压元件[M].北京: 机械工业出版社, 1988.

[2] 路甬祥, 胡大纮.电液比例控制技术[M].北京: 机械工业出版社, 1988.

[3] 侯敏, 王涛, 彭彪.非全周开口滑阀阀口面积快速计算方法[J]. 机床与液压. 2013, 41(9): 91-92.

[4] 冀宏, 傅新, 杨华勇. 几种典型液压阀口过流面积分析及计算[J]. 机床与液压, 2003(5): 14-16.

[5] 雷天觉. 液压工程手册[M]. 北京: 机械工业出版社, 1990.

[6] 汪世益, 毛亚西. 闭式双向变量泵伺服系统的特性分析[J]. 液压与气动, 2013(12): 26-29.

[7] 冀宏, 傅新, 杨华勇. 非全周开口滑阀稳态液动力研究[J]. 机械工程学报, 2003, 39(6):13- 17.

[8] 方文敏, 成琳琳等. 带U形节流槽的滑阀稳态液动力研究[J]. 浙江大学学报, 2010, 44(3)574-579.

[9] 冀宏, 王东升等. 非全周开口滑阀阀口面积的计算方法[J]. 兰州理工大学学报, 2008, 34(3)48-51.

责任编辑：刘海涛

Analysis on the Characteristics of Slope-shaped Spool Valve with Notches

Zhang Youjie, Ni Shouchun

The calculation formula for orifice area of slope-shaped spool valve with notches is deduced and the varying features of orifice area are analyzed; by adopting the method of flow field simulation, the value of steady flow force at valve element in different flow directions is explored. The study shows that there exists obvious disparity for the value of steady flow force along with the different flow directions of oil. When the oil flows into the valve port, the value of steady flow force turns out to be rather low, even dropping to nearly zero.

slope-shaped spool valve with notches; orifice area; steady flow force

K249.3

A

1673-1794(2017)02-0023-03

张友杰，滁州学院机械与汽车工程学院教师，硕士；倪受春，滁州学院机械与汽车工程学院副教授(安徽 滁州 239000)。

滁州学院校级规划项目(2015GH47)

2016-07-03