一种条件属性递减系统的核属性动态更新算法

任 倩, 姚光顺, 胡成祥

一种条件属性递减系统的核属性动态更新算法

任 倩, 姚光顺, 胡成祥

为了解决信息系统在条件属性动态减少情况下的核属性更新问题，本文通过深入分析得到与文献[1]中所给可分辨矩阵等价的二进制可分辨矩阵和求核方法，并分析了条件属性递减对二进制可分辨矩阵的影响，基于此提出了条件属性动态减少时核属性的动态更新算法。该算法对已有的二进制可分辨矩阵进行局部更新得到新的二进制可分辨矩阵，从而更新核属性，避免了重新计算，提高了运算效率。实验结果证明，该算法是正确有效的。

条件属性；递减；二进制可分辨矩阵；核属性

在粗糙集理论的众多研究内容之中，高效的属性约简和求核算法，尤其是动态环境中的高效算法，一直是众多学者探索的目标之一。杨明在文献[1]中提出一种基于改进可分辨矩阵的核增量式更新算法，主要考虑对象动态增加情况下核的更新问题；赖桃桃等认为杨明给出的改进可分辨矩阵中存在不必要的计算，为此在文献[2]中提出一种基于改进可分辨矩阵的核增量式更新算法，该算法具有近线性时间和空间复杂度。文献[3]也在文献[1]的基础之上，提出一种基于决策表的核增量式高效更新算法，降低了算法的时间复杂度和空间复杂度，从而有效地提高了动态更新核的效率以及算法的灵活性；文献[4]提出一种基于可分辨矩阵的核属性快速更新算法，该算法主要考虑对象动态删除情况下核的更新问题；文献[5]在深入分析文献[4]的算法后，提出一种不存储可分辨矩阵的改进核增量式更新算法，主要考虑对象动态删除情况下核的更新问题，该算法与文献[4]的算法一样具有线性时间复杂度，且计算量少于文献[4]算法。以上各种动态算法主要是针对信息系统中对象动态增加或删除情况下核属性的更新问题。文献[6]针对信息系统中条件属性动态增加情况下的核属性动态更新情况进行了讨论。

但在人们认知世界的过程中，除了上述的条件属性递增的情况外，随着人们对属性本质的深入了解，一些不重要的属性将被丢弃，也就存在属性递减的情况。然而目前针对信息系统中条件属性动态递减的高效核属性动态算法设计较少，利用普通方法则需要在条件属性每次递减时重新计算，重复了大量的计算。文献[7]虽然针对这一问题提出了相应的解决办法，但在条件属性每次递减时均需要计算相应的剩余属性集依赖度函数，计算复杂。针对这一问题，本文从二进制可分辨矩阵入手，分析了条件属性递减对二进制可分辨矩阵的影响，提出一种基于二进制可分辨矩阵的条件属性递减的核属性更新算法，从而避免了重新求核。理论分析和实验结果表明，该算法是正确可行的。

1 粗糙集相关概念

定义1[8](决策表)一个决策表S=(U,A,V,f)，其中U是对象的集合，也称为论域，A=C∪D是属性集合，其中C是条件属性，D是决策属性，V是属性值的集合，f:U×A→V是一个信息函数，它指定了U中每一个对象x的取值。

定义3 (上下近似) 给定一个决策表S=(U,A,V,f)，对于任意子集X⊆U和一个等价关系B，我们定义子集X关于知识B的下近似和上近似分别为：B_(X)=∪{Yi|(Yi∈U|IND(B)∧Yi⊆X),B-(X)=∪{Yi|(Yi∈U|IND(B)∧Yi∩X≠φ)

其中，U|IND(B)={X|X⊆U∧∀x∀y∀b(b(x)=b(y))}，是不可分明关系B对U的划分，也是论域U的B基本集的集合。

定义4 (正区域)给定一个决策表S=(U,C∪D,V,f)，设U/D={D1,D2,…,Dk}表示决策属性集D对论域U的划分，U/C={C1,C2,…,Cm}表示条件属性集C对论域U的划分，其中Ci(i=1,2,…,m)称为基本块，称为C关于D的正区域。

证明 根据定义4即可得证。

定理1表明，C关于D的正区域实际上是由在决策属性上取值唯一的基本块的并集组成的；反之，任何在决策属性上取值不唯一的基本块都不在正区域中。

2 可分辨矩阵和求核方法

Hu[9]等学者提出的基于可分辨矩阵的求解核的方法是经典的核求解方法之一，虽然该方法有效地降低了计算量，提高核的求解效率，但是在某些情况下不能计算得到正确的核。叶东毅[10]等针对这一问题给出了改进的可分辨矩阵定义和求核方法，纠正了文献[9]方法的错误，并且该方法可有效地降低计算代价。本文则给出一个与文献[1]等价的二进制可分辨矩阵，并利用新的二进制可分辨矩阵，进行条件属性递减情况下核属性动态更新。

2.1 已有的可分辨矩阵和求核方法

定义6[1]对给定的决策表S=(U,C∪D,V,f)，定义可分辨矩阵M1={mi,j}，其元素为：

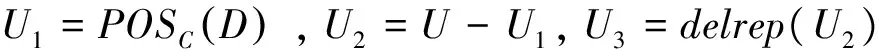
begin

U3=φ;

for任意x∈U2

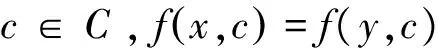
then

U3=U3∪{x};

returnU3;

end

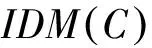
证明 见文献[1].

例1 决策表1S=(U,C∪D,V,f)如表1所示，其中C={c1,c2,c3,c4}是条件属性集，D为决策属性集。

表1 决策表1

对于表1，根据定理1计算可得U1={x1,x2,x5,x6}，U2={x3,x4}，U3=delrep(U2)={x3}。依据定义6建立可分辨矩阵如表2所示。

根据定理2可得，表1的核

表2 决策表1的M1

2.2 等价的二进制可分辨矩阵及求核

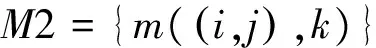
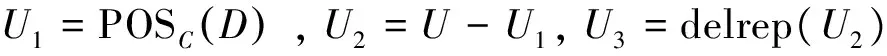
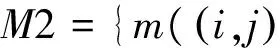
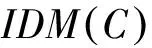
对于表1，根据定义7建立二进制可分辨矩阵如表3所示。

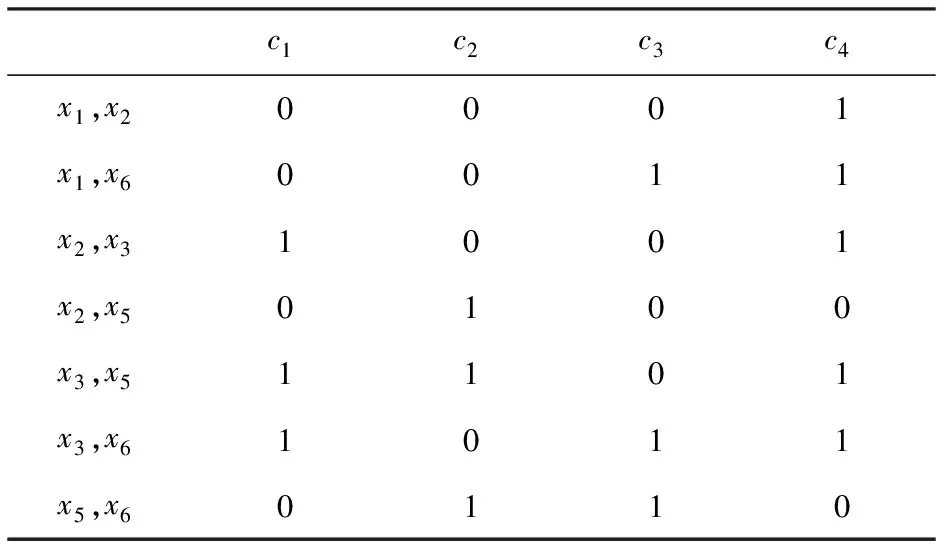
表3 决策表1的M2

上述求解核的方法是针对静态信息系统的，而现实世界是不断变化的，因此研究核属性动态更新算法具有非常重要的实际意义和应用价值。

2.3 核属性动态更新算法

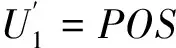
(1)若xi∈U1，xj∈U1，删除条件属性ci之后分以下3种情况：

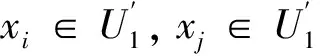
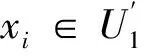
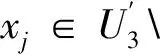
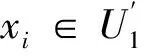
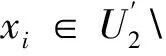
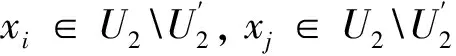
综上，得出条件属性递减系统的核属性更新算法，如算法1所示。

算法1 条件属性递减系统的核属性动态更新算法

输入：S=(U,C∪D,V,f)，M2(C)，U1，U2，U3以及删除的条件属性ci

输出：M2(C(c)i})，Core(C(c)i})

step1 令M2(C(c)i})=M1(C),Core(C(c)i})=φ;

step2 删除M2(C)中ci对应的列，得到的矩阵记为M2'(C);

step4 对M2'(C)作如下更新：

step4.1 if (xi∈U1&&xj∈U1)

step4.3 (xi,xj)所在行保持不变;

step4.5 (xi,xj)所在行保持不变;

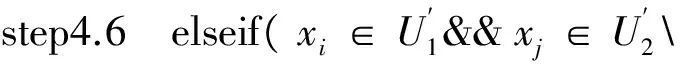
step4.7 删除(xi,xj)所在的行;

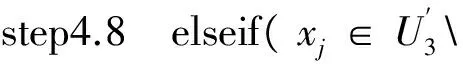
step4.9 新增一行(xi,xj);

step4.11 删除(xi,xj)所在的行;

step4.12 else

step4.13 对M2'(C)不做任何更新;

step4.14 elseif(xi∈U1&&xj∈U3)

step4.16 (xi,xj)所在行保持不变;

step4.18 删除(xi,xj)所在的行;

step4.19 else

step4.20 对M2'(C)不做任何更新;

step4.21 else

step4.22 删除(xi,xj)所在的行;

step5 得到M2(C(c)i});

step6 遍历M2(C(c)i})中的每一行，若该行中只有一个元素的值为“1”，则元素1所在列对应的条件属性U2属于核属性，Core(C(c)i})=Core(C(c)i})∪{ck}

3 实例分析

以例1中的决策表为例，删除条件属性c4之后，计算核属性Core(C(c)4})。

第一步 据U1，U2，U3的定义，计算出

U1={x1,x2,x5,x6}，U2={x3,x4}，U3={x3}，根据M2的定义计算出M2，如前面的表3所示。

第三步 依据算法1，对M2(C(c)4})作如下更新：

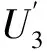
第四步 得到M2(C(c)4})，如表4所示。

第五步 遍历M2(C(c)4})，可知第1、5行中值为1的元素有且只有一个，则其对应条件的属性c2和c3是核属性，即Core(C(c)4})={c2,c3}。

表4 决策表1的M2(C(c)4})

所求得的核属性与文献[1]、文献[7]和文献[10]中算法的结果是相同的。由此证明算法1是正确和可行的。

4 结束语

本文提出一种与文献[1]所给可分辨矩阵等价的二进制可分辨矩阵以及基于该可分辨矩阵的核属性动态更新算法，主要考虑条件属性递减情况下如何快速地求出核属性。该算法在更新二进制可分辨矩阵时，需要删除一列，增加并更新若干行。为条件属性动态删除情况核属性的动态更新提供了一种新的思路。

[1] 杨明.一种基于改进差别矩阵的核增量式更新算法[J].计算机学报,2006,29(3):407-413.

[2] 赖桃桃,冯少荣,张东站.基于改进差别矩阵的核增量式更新算法[J].计算机应用,2009,29(9):2477-2480.

[3] 钱文彬,徐章艳,杨炳儒,等.一种基于决策表的核增量式高效更新算法[J].小型微型计算机系统,2010, 31(4):739-743

[4] 杨明,杨萍.基于差别矩阵的属性核快速更新算法[J].控制与决策, 2007,22(4):453-456.

[5] 冯少荣,赖桃桃,张东站.一种改进的核增量式更新算法[J].计算机工程与应用,2010,46(20):96-98.

[6] 姚光顺,任倩,杨传健,等.条件属性递增系统的核属性动态更新算法[J].计算机工程与应用,2012, 48(7):158-164.

[7] 陈炎龙.基于属性递减策略的属性约简递归算法[J].科学技术与工程,2012,20(24): 6179-6183.

[8] 胡峰,代劲,王国胤.一种决策表增量属性约简算法[J].控制与决策,2007,22(3):268-277

[9] Hu X H, CERCONE N. Learning in relational databases:a Rough Set approach[J]. Computational Intelligence,1995,11(2):323- 337.

[10] 叶东毅,陈昭炯.一个新的二进制可辨识矩阵及其求核的计算[J].小型微型计算机系统,2004,25(6):965-967.

责任编辑：刘海涛

Algorithm for Updating Core Attributes for the Information Systemwith Descending Conditional Attributes

Ren Qian, Yao Guangshun, Hu Chengxiang

In order to solve the problem of updating core attributes for the information system with descending conditional attributes, a binary discernible matrix which is identical to the discernibility matrix that gived in literature[1] is proposed based on in-depth study at first. Then, an algorithm for fast updating core attributes for the information system with descending conditional attributes is given by analyzing the influence caused by the descended condition attributes to the binary discernibility matrix. The algorithm computes new binary discernibility matrix to get core attributes based on the originally binary discernibility matrix and updating its local portion. Because the proposed algorithm avoids calculating the core attributes from very beginning, it can avoid re-calculating and improving the computing speed. The theoretical analysis and experimental results show the proposed algorithm is much more efficient and useful in computing.

condition attribute; descending; binary discernibility matrix; core attribute

TP391

A

1673-1794(2017)02-0008-05

任倩，滁州学院计算机与信息工程学院讲师，姚光顺，滁州学院计算机与信息工程学院副教授，胡成祥，滁州学院计算机与信息工程学院讲师(安徽 滁州 239000)。

滁州学院科研启动项目(2014qd18)，安徽省高校自然科学研究项目(KJ2017A418，KJ2015B19)

2016-08-05