基于贝叶斯推断估计药物动力学模型参数
余晓美, 张海永,沈永昌
基于贝叶斯推断估计药物动力学模型参数
余晓美, 张海永,沈永昌
为克服药理观测数据的不确定性和未知参数高维化给非线性药物动力学模型参数估计带来的困难,基于贝叶斯定理推导了模型参数的后验分布。采用马尔科夫链蒙特卡罗(MCMC)方法对参数的后验分布进行采样,从而获得参数的估计值。抽样方法为延迟拒绝自适应抽样算法(DRAM),实证结果表明,DRAM方法能够对药物动力学模型进行良好的参数估计。对比DRAM算法和常用、经典的Metropolis Hastings(MH)模拟结果,可以发现DRAM算法在求解药物动力学模型参数估计问题具有更小的误差,同时具有稳定、收敛速度更快,高效的特点。
贝叶斯推理;药物动力学模型;DRAM;MCMC
1 前言
药物动力学主要用于建立监测个体的体内药量或药物浓度随时间变化的数学表达式,并求算出有关药动学参数,从而研究药物、毒物及其代谢在体内的吸收、分布、代谢和排泄的动态过程及这些过程与药理反应间的定量规律。结合药动学模型和药动学参数,调整和确定用药方案,保证药物治疗的有效性和安全性[1]。目前用于刻画药物在体内的动力学规律的动力学模型类别多样,从常微分方程到随机微分方程,从房室模型到非房室模型,从线性到非线性模型[2]。非线性药动学参数的计算方法主要有加权非线性最小二乘法进行曲线拟合,Gauss-Newton、Hartley等求导类算法和单纯形算法、遗传算法等非求导类算法[3]。对现实研究而言,经常面临临床实验数据相对比较少,或者是实验条件昂贵,甚至是实验情况不允许大规模进行的情况。由于贝叶斯估计方法不仅能够充分结合模型、数据的信息和参数的先验信息,而且还能对缺失数据进行简明化处理,因此,贝叶斯估计方法在药物动力学研究中具有无语伦比的优势,成为药物动力学参数估计的新兴方法[4]。
马尔科夫链蒙特卡罗(MCMC)方法的提出解决了贝叶斯估计中复杂的后验概率分布积分的数值求解问题,从而将贝叶斯统计方法从理论拓展到了药物动力学、水动力学等非线性高维度模型的应用。为适应更加复杂的现实领域问题的模型参数求解,MCMC方法在基本的Gibbs抽样和Metropolis-Hastings(MH)抽样算法的基础上,发展演化出切变抽样(Slice Sampling)算法、适应性Metropolis(AM)算法、延迟拒绝(DR)算法、延迟拒绝适应性Metropolis(DRAM)算法等。DRAM耦合了DR和AM的优点,被认为在处理非线性、参数高维、参数高度相关的模型,或者是在目标分布远远偏离于高斯分布时有突出的优势[5]。目前,DRAM在国外和国内的药物动力学等领域应用研究都比较少[6]。
本文以非线性药物代谢动力学模型未知参数的贝叶斯估计为目标,结合DRAM算法实现模型反演并获得良好的药物代谢规律的模拟效果。同时,对比DRAM这一新的抽样方法与MH进行对比,为高度非线性、高维模型参数估计提供参考标准。
2 药物代谢动力学模型的贝叶斯参数估计
2.1 药物动力学模型
假设药物的药代动力学满足口服单隔室分布,且模型是非线性吸收动力学及一级消除动力学过程:
(1)
(2)
其中,Q(mg)代表口服药物的药量,C(mg/l)为血浆中的药物浓度,Vmax(mg/min)为体内药物最大转运速率常数,Km称为米氏常数,CL(l/min)为清除速率常数,Vd(l)为表观分布容积,它是联系着体内药量Q与血药浓度C的桥梁。患者服用药物后某一时刻的体内药量无法知道,但是血药浓度可以根据即时抽取的血样测定出来,两者联系的数学公式表示为Vd=Q/C。
药物代谢模型的形式多样。研究表明,许多新的类别的模型如随机微分模型,分数阶模型等的改进和确定都可以基于以上典型常微分药物代谢动力学模型进行。因此,不失一般性,我们的计算模型将以此为例,利用实测的时间-血药浓度的数据构建有效合理的贝叶斯算法,以获取药物代谢动力学特征参数θ=(Vmax,Km,V,CL),为新药的研制、剂量的确定和给药方案的设计提供理论依据。在计算中,记初始药量为Q0=Q(0),初始血药浓度为C0=C(0)。
2.2 模型参数估计的贝叶斯算法
为获取模型特征参数θ=(Vmax,Km,V,CL)的信息,根据贝叶斯原理,可以知道参数的后验分布πpost(θ|Y)满足以下计算公式:
(3)
其中π(θ)为参数θ的先验分布,L(Y|θ)为给定样本观察数据Y的似然函数。由贝叶斯算法的基本原理,参数θ=(Vmax,Km,V,CL)的识别问题将转化为下述给定观测数据Y的统计反问题。
记前向药动力学模型式(1)的解为f(θ),假设观测导致的误差模型表示为

(4)

(5)
根据模型(4),给定n个独立同分布样本观察数据Y=(y1,y2,…,yn)'的似然函数L(Y|θ,σ2)的似然函数可以表示为:
(6)
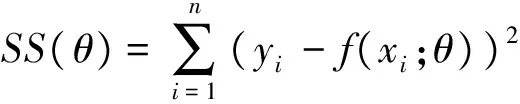
由贝叶斯定理(3),可以推导出所有参数的后验分布为

2.3 DRAM抽样算法
一旦获得了所有参数的后验分布,就可以获得参数的后验特征。然而一般情况下是无法得到其相关的解析形式,因此我们通常借助MCMC抽样算法来实现复杂积分的数值求解。经典的MH算法计算步骤是[5,7]:
1)给出参数初始值θ(0)和建议分布q;
2)从建议分布q(θ(i+1)|θ(i))中抽取变量θ(i+1);
3)以概率α(θ(i+1),θ(i))接受θ(i+1),其中

(7)
4)重复步骤2,直至获取足够的抽样。
显然,M-H算法中建议分布一旦设定变保持不变,研究证明建议分布会影响马尔科夫链的收敛速度,建议分布越接近目标分布,则马尔科夫链收敛越快[1]。马尔科夫链的收敛速度在高非线性和高维参数估计模型中显得尤为重要。在AR算法中采取不断更新建议分布的协方差的方式,使其不断接近目标分布。DR算法采取延迟拒绝抽样值的方式来降低拒绝概率,为了提高效率,Haario等吸收AR和DR的抽样思想,设计提出了DRAM算法[1]。以高斯型建议分布为例,基于药物动力学模型(1)(2)的贝叶斯参数估计的DRAM抽样算法具体步骤如下:

2)DR循环抽样。从建议分布qi(θ*|θ(i))中抽取新的参数θ*,以第1层的接受概率来接受θ*;
3)如果接受θ*,令θ(i+1)=θ*;如果拒绝θ*,令θ(i+1)=θ(i);
4)如果循环次数i>n0,提出新的建议分布的协方差C(i),从而得到更高层的建议分布q,并根据新的建议分布。
5)重复步骤2,直至获取足够的抽样。
3 模型的贝叶斯模拟
在药物动力学模型的参数估计和DRAM抽样算法的模拟中,选取文献中的临床试验数据[8]取参数的初始值为
CL=0.05(l/min),Q0=5(mg),C0=0(mg/l)
样本的时间点取值为1,2,4,6,8,10,15,20,30,40,50,60,70,80,90, 100,150,200,250,300;相应的血药浓度为0.018081,0.035952,0.071065,0.10535,0.1388,0.17145,0.24949,0.32249,0.45305,0.56133,0.64181,0.68151,0.6663,0.61523,0.55859,0.50569,0.3067,0.186,0.1128,0.068409。根据上述贝叶斯算法,进行了10000次迭代,为减少统计误差,舍弃前1000次迭代结果。图1和图2分别给出了MH抽样算法和DRAM抽样算法的迭代过程,显然,DRAM算法相对于MH算法收敛更快,具有更好的混合性。如图3所示,DRAM算法取得良好的参数估计效果。为更细致考察两种抽样算法生成的马尔科夫链的收敛性,表1和表2给出了两种算法相关统计指标的结果。从参数的均值、标准差和估计误差来看, MH算法和DRAM算法都取得了比较好的估计效果。从Geweke检验方法结果来看,两种方法的马尔科夫链均已收敛,收敛程度有微小的差异。从序列的自相关时间间隔(τ)来看,DRAM方法显然更有效率。以参数V的τ值来看,大约每间隔15个取样点能取得独立同分布的样本,而MH算法大约需要每隔20个点采样才能取得独立同分布的样本。

图1 MH抽样算法参数估计的迭代过程和误差

图2 DRAM抽样算法参数估计的迭代过程和误差
表1 MH算法模拟的统计数据

参数均值标准差估计误差τGewekeVmax0.110610.0039250.0001272215.0410.99615Km0.764050.137410.004920716.5880.97035V4.94680.0795320.0031120.6570.99522CL0.0502060.000727093.0009e⁃00515.9720.99817

表2 DRAM算法模拟的统计数据

图3 DRAM抽样算法模型参数拟合效果
4 结论
本文针对非线性药物动力学模型的参数估计问题,给出了MCMC的DRAM算法,仿真结果表明:MCMC算法能够很好解决药物动力学模型的参数估计问题,为药理分析和药物临床试验提供较好的参考,药物动力学模型拟合结果和实测结果拟合效果良好,说明了用MCMC及其相关方法应用于药物动力学模型的有效性;结果显示DRAM算法具有更好的灵活性和高效性,在收敛速度和混合性方面都具有明显的优势,适合用在高度非线性和高维参数估计模型中。因此,基于DRAM
算法的非线性药物动力学模型反演结果能在现实应用中具有重要的价值。
[1] 张萍, 陆涛, 言方荣等. 基于随机微分方程的群体药物代谢动力学参数的极大似然估计 [J]. 药学研究, 2013, 26(3), 304-309.
[2] 曾文艺,孙晓颖. 药物动力学房室模型的改进[J]. 北京师范大学学报(自然科学版), 2010, 46(5): 541-545.
[3] 蔡晔,孙春萌,沈雁. 非线性药物动力学参数的计算方法研究进展[J]. 药学研究, 2014, 33(7), 401-404.
[4] Fanni Natanegara,Beat Neuenschwander,John W, Seamen et al. The current state of Bayesian methods in medical product development: survey results and recommendations from the DIA Bayesian scientific working group[J]. Pharmaceutical Statistics, 2014, 13:3-12.
[5] Marko Lain. Adaptive MCMC methods with applications in environmental and geophysical models[D]. Finland, 2008,12-14.
[6] 张庆庆, 许月萍, 张徐杰等. 基于DRAM的水质模拟不确定分析和风险决策[J]. 浙江大学学报(工学版), 2012, 46(12): 2231-2236,2242.
[7] Zuev K M, Katafygiotis I S. Modified Metropolis-Hastings algorithm with delayed rejection[J]. Probability Engineering Mechanics,2011, 26(3): 405-412.
[8] 褚娟. 利用随机微分方程建立药物代谢动力学模型及其应用[D]. 华中科技大学, 2012.
责任编辑:刘海涛
Application of Bayesian Inference to Estimate the Parametersin Pharmacokinetics Model
Yu Xiaomei, Zhang Haiyong, Shen Yongchang
To overcome the parameter estimation's difficulty from the measurement uncertainty and high dimensions of unknown parameters, mathematical model of posterior probability distribution based on Bayesian inference was set up to estimate the parameters in pharmacokinetics model. Markov chain Monte Carlo(MCMC) method is used to explore the posterior distribution to get the estimation. Delay Rejection Adaptive MCMC is used during sampling. The results show that DRAM method could give a better estimate results comparison to traditional sampling MCMC method such as Metropolis Hastings(MH). DRAM method has been proved to be more stable and effective than MH for pharmacokinetics parameters calculation.
Bayesian inference; Pharmacokinetics model; DRAM; MCMC
O212.8;R969.1
A
1673-1794(2017)02-0004-04
余晓美,滁州学院数学与金融学院讲师,博士,研究方向:应用统计;张海永,沈永昌,滁州学院数学与金融学院(安徽 滁州 239000)。
安徽省人才基金项目(1408085QA06,KJ2014A180);滁州学院科研启动项目(2012qd04);滁州学院科学研究项目(2015GH34)
2016-12-07

