相似与解直角三角形

张继海

一、选择题

1.如图1，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为F，连接DF.给出下列四个结论：① △AEF∽△CAB； ② CF = 2 AF ； ③ DF = DC ；④ tan∠CAD =[2].其中正确的结论有（ ） [A][B][C][D][E][F][A][B][C][E][O][D][图1 图2]

A.4个 B.3个

C.2个 D.1个

2.如图2，D，E分别是△ABC的边AB，BC上的点，且DE∥AC，AE，CD相交于点O，若S△BDE∶S△CDE = 1∶2，则S△DOE与S△COA的比是（ ）

A.1∶3 B.1∶16

C.1∶4 D.1∶9

3.如图3，在正方形网格中，每个小正方形的边长均相等.网格中三个多边形（分别标记为①②③）的顶点均在格点上.被一个多边形覆盖的网格线中，竖直部分线段的长度之和记为m，水平部分线段的长度之和记为n，则这三个多边形中满足m = n的是（ ） [＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&][①][②][③][图3]

A.只有② B.只有③

C.②③ D.①②③

4.如图4，在△ABC中，AD和BE是高，∠ABE = 45°，点F是AB的中点，AD与FE，BE分别交于点G，H，∠CBE =∠BAD.给出下列结论：① FD = FE；② AH = 2 CD；③ BC·AD =[2]AE2；④ S△ABC = 4 S△ADF.其中正确的结论有（ ） [A][B][C][D][E][F][G][H][图4 ]

A.1个 B.2 个

C.3 个 D.4个

5.已知抛物线y =-x2-2x + 3与x轴交于A，B两点，将这条抛物线的顶点记为C，连接AC，BC，则tan∠CAB的值为（ ）

A.[12] B.[55]

C.[255] D.2

6.如图5，点D（0，3），O（0，0），C（4，0）在⊙A上，BD是⊙A的一條弦，则sin∠OBD =（ ）

A.[12] B.[34]

C.[45] D.[35][O][x][y] [A][B][C][D][·] [A][B][C][D][E][F][G][P][Q][图5 图6]

7.如图6，在正方形ABCD中，E，F分别为BC，CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA的延长线于点Q.给出下列结论：① AE = BF； ② AE⊥BF； ③ sin∠BQP =[45]； ④ S四边形ECFG = 2 S△BGE.其中正确的结论有（ ）

A.4 个 B.3 个

C.2个 D.1个

8.如图7，在4×4的正方形方格图形中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则图中∠ABC的余弦值是（ ）[＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&] [A][B][C][图7]

A.2 B.[255]

C.[12] D.[55]

9.如图8，在Rt△ABC中，∠B = 90°，∠BAC = 30°，以点A为圆心，BC长为半径画弧交AB于点D，分别以点A，D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠EAD的余弦值是（ ） [A][B][C][图8] [M][D][E]

A.[312] B.[36]

C.[33] D.[32]

10.如图9，某办公大楼正前方有一根高度是15米的旗杆ED，从办公楼顶端A测得旗杆顶端E的俯角a 是45°，旗杆底端D到大楼前梯坎底边的距离DC是20米，梯坎坡长BC是12米，梯坎坡度i = 1∶[3]，则大楼AB的高度约为（精确到0.1米，参考数据：[2]≈1.41，[3]≈1.73，[6]≈2.45）（ ） [A][B][C][D][E][α][图9]

A.30.6 B.32.1 C.37.9 D.39.4

二、填空题

11.如图10，正方形ABCD的边长为3，连接AC，AE平分∠CAD，交BC的延长线于点E，FA⊥AE，交CB的延长线于点F，则EF = . [A][B][C][D][E][F][图10]

12.如图11，在矩形ABCD中，AB =[3]，BC =[6]，点E在对角线BD上，且BE = 1.8，连接AE并延长交DC于点F，则[CFCD]= . [A][B][C][D][E][F] [A][B][C][D][图11 图12]

13.如图12，在四边形ABCD中，∠ABC = 90°，AB = 3，BC = 4，CD = 10，DA =[55]，则BD的长为 .

14.⊙O的半径为1，弦AB =[2]，弦AC =[3]，则∠BAC的度数为 .

15.如图13，在正方形ABCD外作等腰直角

△CDE，DE = CE，连接BE，则tan∠EBC = . [A][B][C][D][E][图13]

三、解答题

16.在△ABC中，P为边AB上一点.

（1）如图14，若∠ACP =∠B，求证：AC2 = AP·AB；

（2） 如图15，若M为CP的中点，AC = 2，∠PBM =∠ACP，AB = 3，求BP的长. [A][B][C][P][A][B][C][P][M][图14 图15]

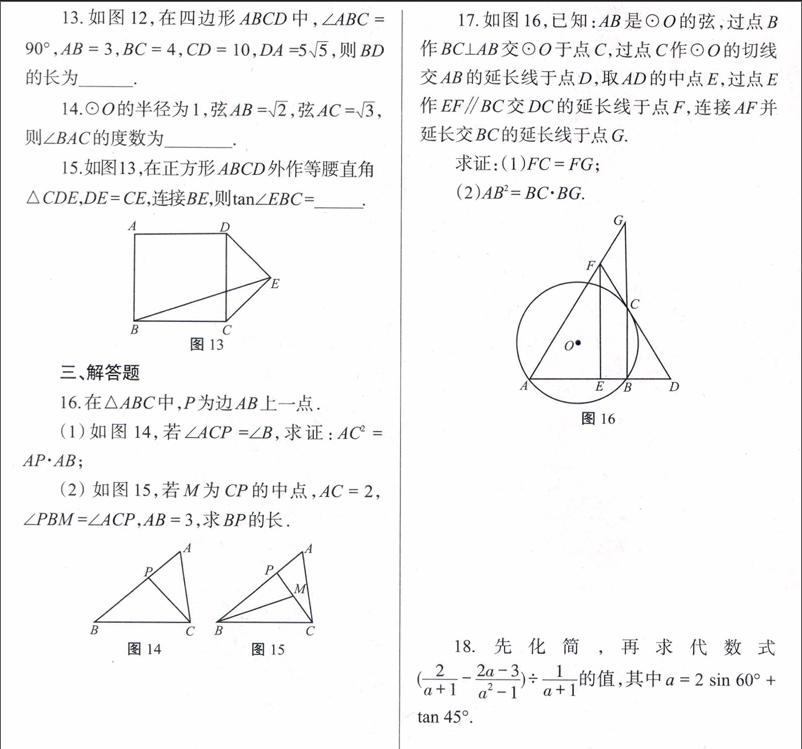
17.如图16，已知：AB是⊙O的弦，过点B作BC⊥AB交⊙O于点C，过点C作⊙O的切线交AB的延长线于点D，取AD的中点E，过点E作EF∥BC交DC的延长线于点F，连接AF并延长交BC的延长线于点G.

求证：（1）FC = FG；

（2）AB2 = BC·BG. [A][B][C][D][E][F][G][O][·][图16]

18.先化简，再求代数式[（2a+1-2a-3a2-1）÷1a+1]的值，其中a = 2 sin 60° + tan 45°.

19.如图17，△ABC和△BCE均为等腰直角三角形，且∠ACB =∠BEC = 90°，AC = 4[2]，点P为线段BE延长线上一点，连接CP以CP为直角边向下作等腰直角△CDP，线段BE与CD相交于点F. [A][B][C][D][E][F][P][圖17]

（1）求证：[PCCD=CECB].

（2）连接BD，请你判断AC与BD有什么位置关系？并说明理由.

（3）设PE = x，△PBD的面积为S，求S与x之间的函数关系式.

20.某班数学兴趣小组利用数学活动课时间测量位于小山山顶的炎帝雕像高度，如图18，已知该山坡面与水平面的夹角为30°，山高857.5尺，组员从山脚D处沿山坡向着雕像方向前进1 620尺到达点E，在点E处测得雕像顶端A的仰角为60°，求雕像AB的高度. [A][B][C][D][E][图18]

21.如图19，天星山山脚下西端A处与东端B处相距800（1 +[3]）米，小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°，东端的坡角是30°，小军的行走速度为[22]米/秒.若小明与小军同时到达山顶C处，则小明的行走速度是多少？ [A][B][C][45°][30°][图19]

22.如图20，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB = 80 m，DE = 10 m，求障碍物B，C两点间的距离是多少（参考数据：[2]≈1.41，[3]≈1.73，结果精确到0.1 m）？ [A][B][C][图20] [D][E] [30°][45°]