四边形的认识与证明

韩敬

一、选择题

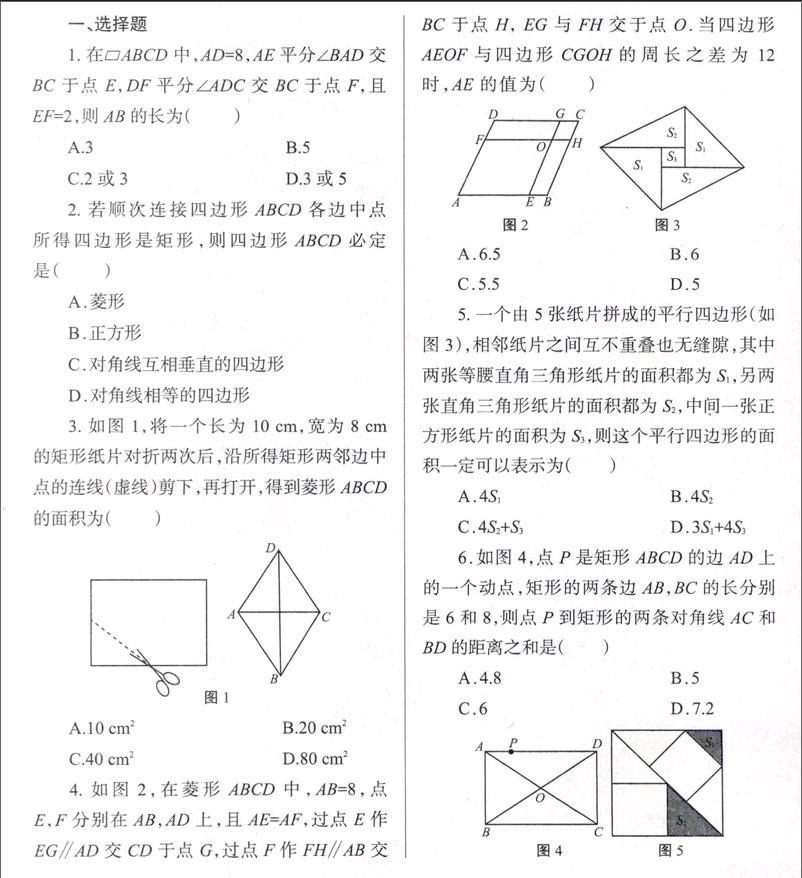
1. 在[?]ABCD中，AD=8，AE平分∠BAD交BC于点E，DF平分∠ADC交BC于点F，且EF=2，则AB的长为（ ）

A.3 B.5

C.2或3 D.3或5

2.若顺次连接四边形ABCD各边中点所得四边形是矩形，则四边形ABCD必定是（ ）

A.菱形

B.正方形

C.对角线互相垂直的四边形

D.对角线相等的四边形

3.如图1，将一个长为10 cm，宽为8 cm的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再打开，得到菱形ABCD的面积为（ ） [A][B][C][D][图1]

A.10 cm2 B.20 cm2

C.40 cm2 D.80 cm2

4. 如图2，在菱形ABCD中，AB=8，点E，F分别在AB，AD上，且AE=AF，过点E作EG∥AD交CD于点G，过点F作FH∥AB交BC于点H， EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时，AE的值为（ ） [A][B][C][D][E][F][G][H][O][图2 图3] [S1][S2][S3][S1][S2]

A.6.5 B.6 C.5.5 D.5

5. 一个由5张纸片拼成的平行四边形（如图3），相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1，另两张直角三角形纸片的面积都为S2，中间一张正方形纸片的面积为S3，则这个平行四边形的面积一定可以表示为（ ）

A.4S1 B.4S2

C.4S2+S3 D.3S1+4S3

6.如圖4，点P是矩形ABCD的边AD上的一个动点，矩形的两条边AB，BC的长分别是6和8，则点P到矩形的两条对角线AC和BD的距离之和是（ ）

A.4.8 B.5

C.6 D.7.2 [A][B][C][D][O][P][·] [S1][S2][图4 图5]

7.有3个正方形如图5放置，阴影部分的面积依次记为S1，S2，则S1∶S2等于（ ）

A.1∶[2] B.1∶2

C.2∶3 D.4∶9

8.如图6，在四边形ABCD中，∠ABC=90°，AB=BC=[22]，E，F分别是AD，CD的中点，连接BE，BF，EF.若四边形ABCD的面积为6，则△BEF的面积为（ ）

A.2 B.[94]

C.[52] D.3 [A][B][C][D][E][F][A][B][C][D][E][F][B′][图6 图7]

9. 如图7，在矩形ABCD中，AB=4，AD=6，E是AB边的中点，F是线段BC上的动点，将△EBF沿EF所的在直线折叠得到△EB′F，连接B′D，则B′D的最小值是（ ）

A.[210-2] B.6

C.[213-2] D.4

二、填空题

10.如图8，在[?]ABCD中，AB=[213]cm，AD=4 cm，AC⊥BC，则△DBC比△ABC的周长长 cm. [A][B][C][D][图8]

11.如图9，菱形ABCD的面积为120 cm2，正方形AECF的面积为50 cm2，则菱形的边长为 cm. [A][B][C][D][E][F][图9]

12.如图10，在Rt△ABC中，∠B=90°，AB=4，BC>AB，点D在BC上，以AC为对角线的所有平行四边形ADCE中，DE的最小值是 . [A][B][C][D][E][F][O][A][B][C][D][E][图10 图11]

13.如图11，在正方形ABCD中，AD=5，点E，F是正方形ABCD内的两点，且AE=FC=3，BE=DF=4，则EF的长为 .

14. 如图12，一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是 . [A][B][C][D][E][·][图12]

三、解答题

15.在方格纸中，点A，B，P都在格点上.请按要求画出以AB为边的格点四边形，使点P在四边形内部（不包括边界），且点P到四边形的两个顶点的距离相等.

（1）在图13中画出一个[?]ABCD.

（2）在图14中画出一个四边形ABCD，使∠D=90°，且∠A≠90°.[＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&][＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&＼&][A][B][P][A][B][P][·][·] [图13 图14]

16.如图15，在矩形ABCD中，点F在边BC上，且AF=AD，过点D作DE⊥AF，垂足为点E.

（1）求证：DE=AB；

（2）以A为圆心，AB长为半径作圆弧交AF于点G，若BF=FC=1，求扇形ABG的面积（结果保留π）. [A][B][C][D][E][F][G][图15]

17.如图16，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点，点M是AB边上的一个动点（不与点A重合），延长ME交CD的延长线于点N，连接MD，AN. [A][B][C][D][E][M][N][图16]

（1）求证：四边形AMDN是平行四边形.

（2）填空：①当AM的值为 时，四边形AMDN是矩形；

②当AM的值为 时，四边形AMDN是菱形.

18.已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF=60°.

（1）如图17，当点E是线段CB的中点时，直接写出线段AE，EF，AF之间的数量关系；

（2）如图18，当点E是线段CB上任意一点时（点E不与B，C重合），求证：BE=CF； [A][B][C][D][E][F] [A][B][C][D][E][F][图17 图18]

（3）如图19，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离. [A][B][C][D][E][F][图19]

19.（1）问题情境：

如图20，在正方形ABCD中，E，F，G，H分别为AB，BC，CD，DA边上的动点，连接EG，HF相交于点O，且∠HOE=∠D.试判断：EG与FH的数量关系，不要说明理由. [A][B][C][D][E][F][G][H][O][A][B][C][D][E][F][G][H][O][图20 图21]

（2）拓展延伸：

如图21，在菱形ABCD中，E，F，G，H分别为AB，BC，CD，DA边上的动点，连接EG，HF相交于点O，且∠HOE=∠D，试探究：（1）中EG与FH的数量关系还成立吗？请说明理由.

（3）反思提升：

若将（2）中的菱形ABCD改为平行四边形ABCD（如图22），AB=a，AD=b，其他条件不变，则[EGFH=ba]的猜想正确吗？请说明理由.