浅析用基本不等式求函数最值

广东省惠东县惠东中学 李 莎

基本不等式：若实数a＞0,b＞0,则（当且仅当a=b时取等号）

在使用基本不等式时，要注意把握四个方面，即“一正，二定，三相等，四同时”。一正即各项都是正实数；二定即和为定值或积为定值；三相等即等号能否取得到，若取不到，可以利用“对勾函数“的单调性解题；四同时即多次使用基本不等式，等号要同时成立。

一、利用基本不等式求最值要注意条件的验证

若x＞0时，满足不等式条件，可以直接利用基本不等式求最值；若x＜0时，需要先转化成-x＞0，才能利用基本不等式求最值。

例1 若x＞0，求函数的值域.

解：因为x＜0，所以-x＞0，则

因为所以f( x) ≤ -12，当且仅当时，即x=-2时，故f(x)函数的值域为(-∞,-12].

二、通过代数变换配凑成使用基本不等式的形式

通常会出现“二次比一次”，“一次比二次”，“二次比二次”这三种类型.（1）对于“二次比一次”和“一次比二次”的类型，基本思路都是对一次函数整体换元，求出新的变量的范围，转化为对勾函数；（2）对于“二次比二次”的类型，一般先分离常数，然后转化成一次比二次的类型，再来求解。.

例2 已知求的最小值.

解：令则，代回原式可得，

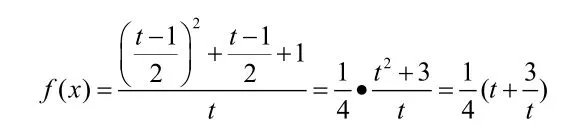
三、“1”的变换或正常数a的变换

利用题目中的条件“1”或正常数a代换成给定的代数式，然后将需求解的函数乘以该代数式，化成可以使用基本不等的形式。

例3 已知且，求x+y的最小值.

解：因为，所以

=当且仅当即时，

四、在求二元函数最值中应用转化思想和方程消元思想

例4 若实数满足求a+b的最小值。由等量关系可知，只要将需要求解的部分a+b之外的部分利用不等式转化为所求形式，然后解不等式即可。

解法一（基本不等式）：由当且仅当a=b时取等号.令则整理得解得或（舍去），即，此时，a=b=3.

解法二（判别式法）：令代入原式得，整理得：解得（舍去），，解得a=b=3满足题意，即

五、灵活选择和运用基本不等式的变式

要灵活选择和运用基本不等式，主要在于能观察出所求式子与题目中给的条件的联系，运用基本不等式灵活建立两者之间的联系。

例5 设求的最大值.以

解：因为所

，当且仅当时等号成立，解得

故

纵观上述求函数最值五种类型，在使用基本不等式时，一定都要把握住四个方面，即“一正，二定，三相等，四同时”。这四个方面缺一不可，若忽略了某个条件的检验，都有可能会出现。