从不同的视角解决《电磁学》问题*

信江波，李春雷，刘 芳，吴淑杰，俞 莹

(东北林业大学)

从不同的视角解决《电磁学》问题*

信江波，李春雷，刘 芳，吴淑杰，俞 莹

(东北林业大学)

物理概念的掌握和数学方法的选择是解决《电磁学》问题的两个主要方面.以两道习题为例，来说明不同的视角分析和解决《电磁学》问题的重要性.

视角;电场强度;电位;积分

0 引言

在《电磁学》教学中，引导学生从不同的视角分析和解决问题，可以加深学生对《电磁学》问题的理解，开阔学生思路，培养发散性思维，从而提高学生解决实际问题的能力.通常不会做的题多半是没有掌握该题的正确物理概念，或者没有选择适当的数学方法进行计算.下面以两道典型的电磁学习题为例，阐述一下从不同的视角分析和解决问题的重要性.

例1 如图1所示，在半径为R1和R2的两个同心球面上，分别均匀地分布着电量为Q1和Q2的电荷，试求当Q1=－Q2时，Ⅰ、Ⅱ、Ⅲ三个区域内电位的分布情况.

视角一

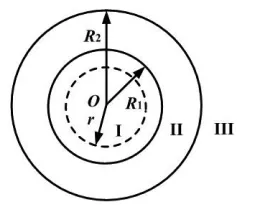
图1

从电位的定义视角出发，先求解空间各区域的电场强度，再由电场力做功求解出电位的分布情况.

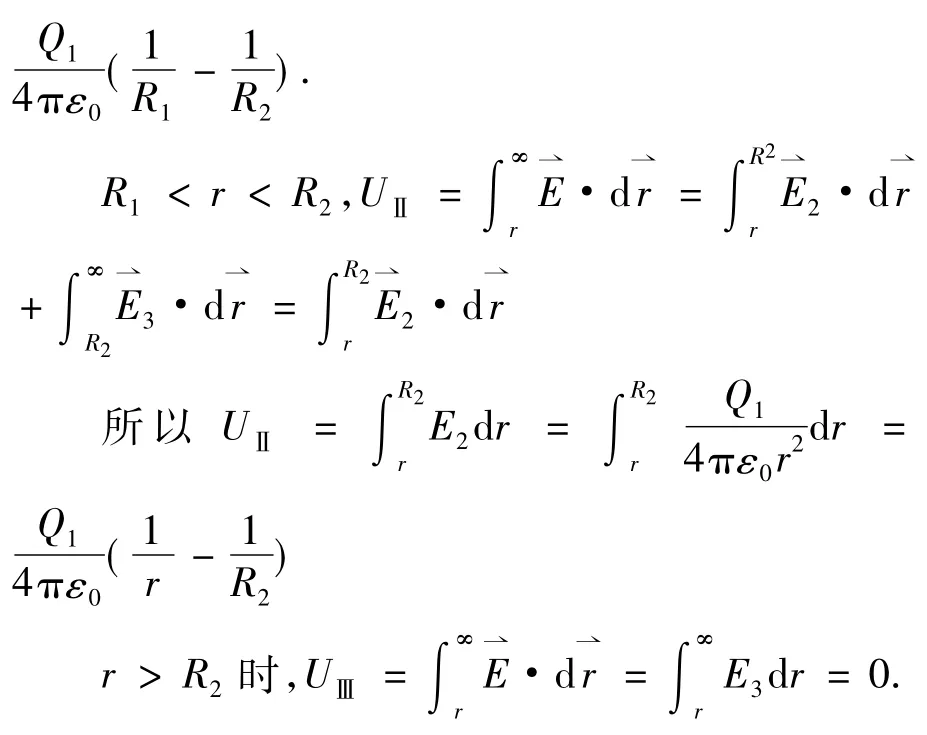
视角二

从电位叠加原理视角出发，先求解各带电体在空间的电位，再进行叠加求解出各区域的电位分布情况.

半径为R1的带电球面在空间的电位分布:

r≤R1时，带电球面处于静电平衡状态，球面及内部空间为一个等位体，则

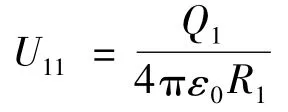
r＞R1时，带电球面类似于一个点电荷，则

半径为R2的带电球面在空间电位分布:

r≤R2时，带电球面处于静电平衡状态，球面及内部空间为一个等位体，则

r＞R2时，带电球面类似于一个点电荷，则

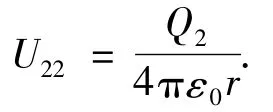
由电位叠加原理，Ⅰ区域的电位为两球面在该区域电位的叠加，则

Ⅱ区域的电位也为两球面在该区域电位的叠加，则

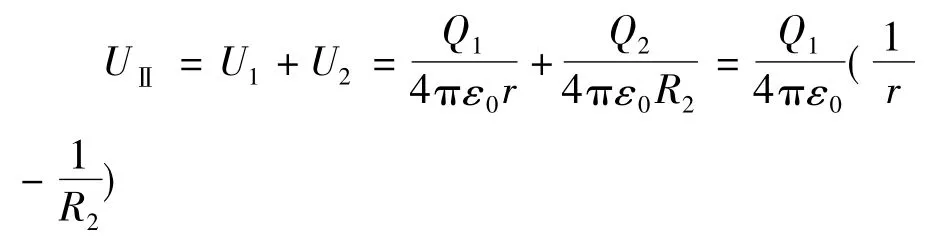
同理，Ⅲ区域的电位为

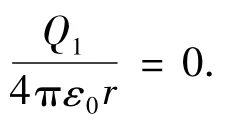
该题分别从电位的定义和电位叠加原理两个视角出发，求解电位在空间的分布情况.第一个视角需要学生理解电位的概念，以电场力做功为基础，把单位正电荷从该点移到电位为零点电场力做的功即为该点的电位，思路简单，积分是主要的计算手段，计算过程略为复杂.第二个视角需要学生在学会电位定义的基础上，理解电位叠加原理，带电体在空间的电位具有独立性，先求解出每个带电体的电位，再进行叠加得到空间的电位分布.带电体的电位与导体的静电平衡状态和点电荷的电位有关，等位体和点电荷的电位可以作为已知条件直接应用，所以只需要简单的加减计算，计算过程简单.

例2一个半径为R的均匀带电半圆环，电荷线密度为λ，试求带电细环环心处O点的电场强度.

分析:根据电场强度叠加原理来求解，先计算出环上电荷元dq在环心处产生的电场强度dE，再对dE进行叠加，即可求解出带电细环环心处O点的电场强度.把积分对象作为视角，选择不同的积分对象，分析它对求解问题的影响.

设半径R与x轴的夹角为φ，则电荷元所带的电量为

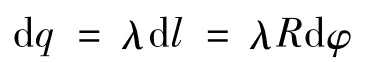
根据库仑定律，电荷元dq在环心产生的电场强度为

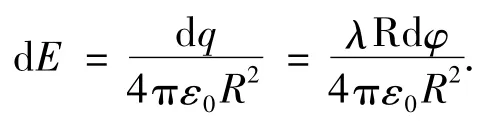
由于每个电荷元在O点产生的电场强度dE的方向不一致，所以不能直接叠加，需要把dE沿着x轴和y轴两个方向分解之后再进行叠加(如图2所示).

dE在 x轴和 y轴的分量分别是 dEx= dEcosφ，dEy=dEsinφ.

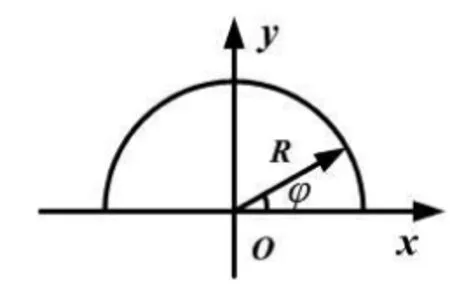
图2

解法1:选择角度φ作为积分对象，可得

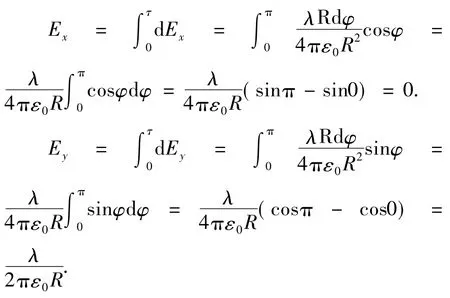
解法2 选择纵坐标y作为积分对象，可得

解法3 选择弧长l作为积分对象，可得

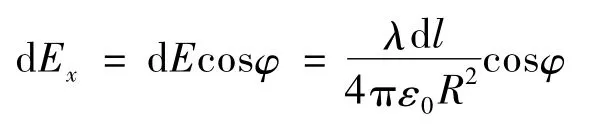
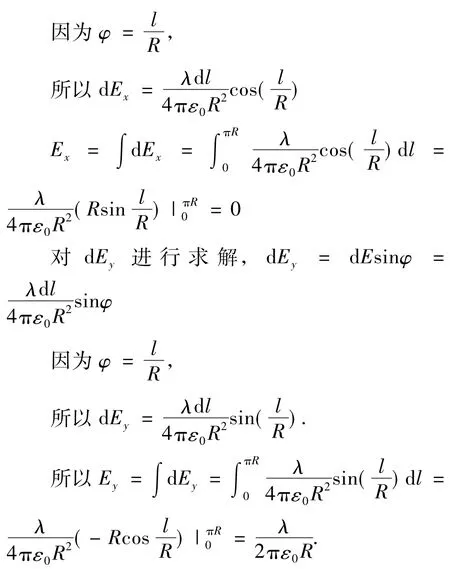
该题分别从角度φ、纵坐标y和弧长l三个视角进行积分求解.对角度φ积分的计算思路清晰，过程简单.对纵坐标y和弧长l积分时，变换积分对象容易出现错误，计算过程比较复杂.应用数学工具时，选择最简便的计算方法，可以节约时间，提高正确率.

该文给出了两道《电磁学》习题的详细求解过程，意在让学生学会从不同的视角分析和解决问题.掌握正确的物理概念，选择适当的数学方法，《电磁学》问题就会迎刃而解.

［1］赵凯华，陈熙谋.电磁学［M］.北京:高等教育出版社，2011.67.

［2］张之翔.电磁学千题解［M］.北京:科学出版社，2008.45.

Solving the Electromagnetic Problems from Different Perspectives

Xin Jiangbo，Li Chunlei，Liu Fang，Wu Shujie，Yu Ying

(Northeast Forestry University)

The physical concepts and the mathematical methods are the two main aspects of solving the electromagnetic problems.Two exercises are taken to explain the importance of electromagnetic problems to be analyzed and solved from different perspectives.

Perspective;Electric field intensity;Electric potential;Calculus

O441

:A

:1000－5617(2017)01－0095－03

(责任编辑:季春阳)

2016－12－19

*2015年度东北林业大学重点课程建设项目资助