基于均匀线阵的自适应单脉冲两目标分辨技术

刘二平，鲁振兴

(1.海军驻保定地区航空军事代表室，河北 保定 071000；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

基于均匀线阵的自适应单脉冲两目标分辨技术

刘二平1，鲁振兴2

(1.海军驻保定地区航空军事代表室，河北 保定 071000；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

自适应单脉冲是相控阵跟踪雷达存在副瓣干扰情况下常用的一种测角技术。在均匀线性阵列条件下，分析了自适应和差波束加权的基本方式，并证明了自适应单脉冲比为实数。雷达主瓣内存在两目标的情况下，基于自适应单脉冲比的实数性质，提出了一种基于双采样点的目标角度测量方法，并对单脉冲比的测量误差进行了分析。仿真结果表明，该方法可实现对两个不可分辨目标的角度估计，估计精度随两采样时刻相位差的不同产生变化。

自适应单脉冲；均匀线阵；不可分辨目标；角估计

0 引言

当相控阵雷达[1]处于跟踪模式时，一般采用单脉冲方法对目标角度进行测量[2]，而在副瓣干扰存在的情况下，需要进行自适应波束形成[3]，传统单脉冲技术测角效果变差，此时，文献[4-6]采用了自适应单脉冲的方法进行测角。然而，单脉冲技术的一个缺点就是无法对同一距离和多普勒单元内的2个或多个目标进行分辨。

对于2个目标情况下的常规单脉冲角度测量，国内外很多学者已经进行了相关的研究。Kanter[7]曾指出如果2个目标回波幅度稳定并且相对相位符合[0,2π]均匀分布，那么单脉冲比的均值将会指向回波较强的目标。如果2个目标均为瑞利目标，那么单脉冲比的均值将会指向2个目标的功率重心。当2个瑞利目标的相对RCS已知时，Blair[8]和Wang[9]分别利用不同的方法得到了2个目标的角度。这2种方法都是基于目标RCS统计特性的，因此需要足够多并且能够反映目标RCS起伏特性的采样点。文献[10]提出了一种基于粒子群的多目标分辨方法。文献[11]提出了一种基于单个脉冲的2个目标角度估计方法，然而，该方法并不适用于一维阵列。

在常规单脉冲体制下，文献[12]曾提出一种基于双采样点的两稳定目标分辨方法，本文将把该方法推广至自适应单脉冲的情况。需要注意的是，虽然文献[13-15]采用空间谱估计的方法对多个目标进行分辨，但该类方法通常在相关处理之前就需要较高的输入信噪比[16]，另外，当同一波束的不同距离速度单元存在多个目标时，该方法很难进行目标和角度之间的关联。

1 自适应单脉冲的基本特性

1.1 阵列模型

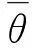
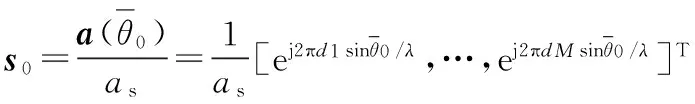
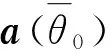
根据MVDR[18]的基本原理，自适应和、差波束的加权矢量可以分别表示为：

(1)

和

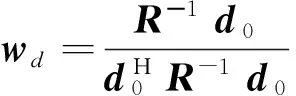
(2)

假设天线阵元接收到目标a和b的回波信号Sa(n)和Sb(n)，两目标入射方向θa和θb均位于接收波束的主瓣。和差通道内的两目标信号可以分别表示为：

以及

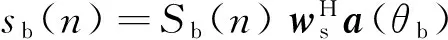
令

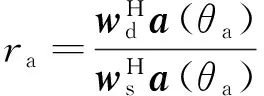
(3)

(4)

于是，差通道中的信号da(n)=rasa(n)，db(n)=rbsb(n)。

1.2 自适应单脉冲比的实数性证明

在均匀线阵中，假设阵元位置di是以阵列中心为原点的，即d1=-dM，d2=-dM-1，…，那么，对于任意2个角度θ1和θ2，有

Im[aH(θ1)a(θ2)]=0，

(5)

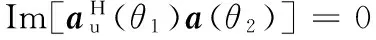
(6)

其中Im[·]代表求虚部。

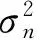
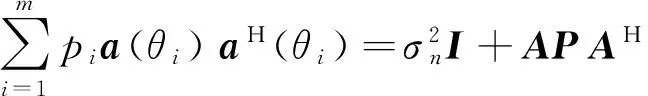
式中，

A=[a(θ1),…,a(θm),a(θa),a(θb)]；

P=diag{p1,…,pm,pa,pb}。

根据矩阵求逆引理[19]，有

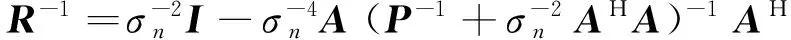
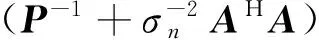
为表示方便，令θm+1=θa，θm+2=θb，

于是，对于式(3)给出的和波束加权向量，有

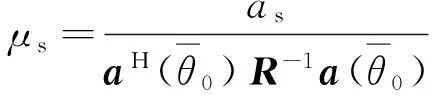
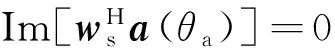
2 两目标分辨方法

2.1 自适应单脉冲比测量方法

假设经过自适应波束形成，脉冲压缩以及相参积累之后，目标信噪比足够高。在进行测角时，暂时不考虑通道中的干扰和噪声成分，于是可以将和、差通道信号表示为：

ys(n)=sa(n)+sb(n)，

yd(n)=rasa(n)+rbsb(n)。

如果在n1和n2时刻，目标回波sa(n)和sb(n)的幅度不变，那么这2个时刻的接收信号可以表示为：

式中，下标1和2分别代表时刻n1和n2；φa1，φa2，φb1和φb2分别代表目标a和b的回波在n1和n2时刻的相位。

因为ra和rb均为实数，所以，经过整理可以得到一个一元二次方程[12]，求出ra和rb之后，根据相应的单脉冲公式就可以求得目标角度(假设目标对单脉冲特性的影响较小)。

需要注意的是上述方法中的“采样点”也可以代表不同的相参积累周期，只要积累时间相同，可以保证目标积累后的幅度稳定即可。

2.2 测量误差分析

上面的求解过程没有考虑噪声的影响，真实情况中噪声是存在的。为简化分析，假设和、差通道中的噪声(这里将通道中的噪声与干扰之和统称为噪声)是不相关的。

实际上和、差通道中的干扰成分存在一定的相关性，但理想情况下自适应波束的零点深度与干扰功率的平方成正比[20]，强干扰可以得到足够的抑制。另外，在自适应和差波束主瓣形变很小的情况下，可以认为波束加权矢量与差波束加权矢量是近似正交的。如果各阵元通道的内部噪声是独立同分布的，那么波束形成之后和差通道内的噪声就近似不相关。所以，可以认为和、差通道中的噪声(与干扰之和)不相关。

假设和、差通道噪声为零均值的复高斯过程。将n1和n2时刻和、差通道中噪声引起的扰动表示为Δys1，Δyd1，Δys2和Δyd2。对一元二次方程的解进行一阶泰勒展开，可以得到ra的估计误差如下：

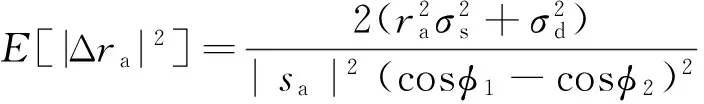
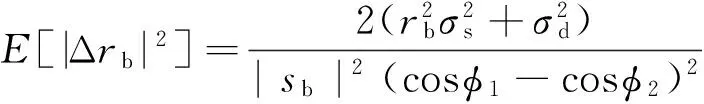
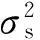
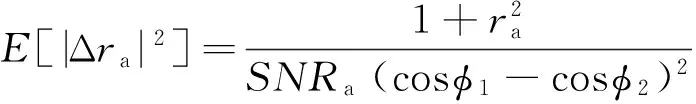
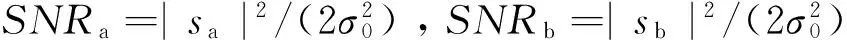
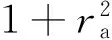
综上可知，cosφ1-cosφ2的大小正比于q2，即n1和n2时刻和通道信号功率之差。所以，在实际中能够获得多个采样点的情况下可以选取功率之差较大的那些点进行目标的角度测量。

3 仿真验证

3.1ra和rb估计的偏差与均方根误差

下面通过仿真对算法的性能进行分析。仿真中，假设|sb|=2|sa|,ra=0.15，rb=-0.2，和、差通道中噪声不相关，并且功率相等。

假设φ1=0°，当φ2在80°～280°变化时，图1和图2给出了经过1 000次蒙特卡洛仿真得到的ra和rb估计的均值偏差和均方根误差(RMSE)(当φ2更加接近φ1时估计的性能会明显变差，这里没有给出相应的结果)。

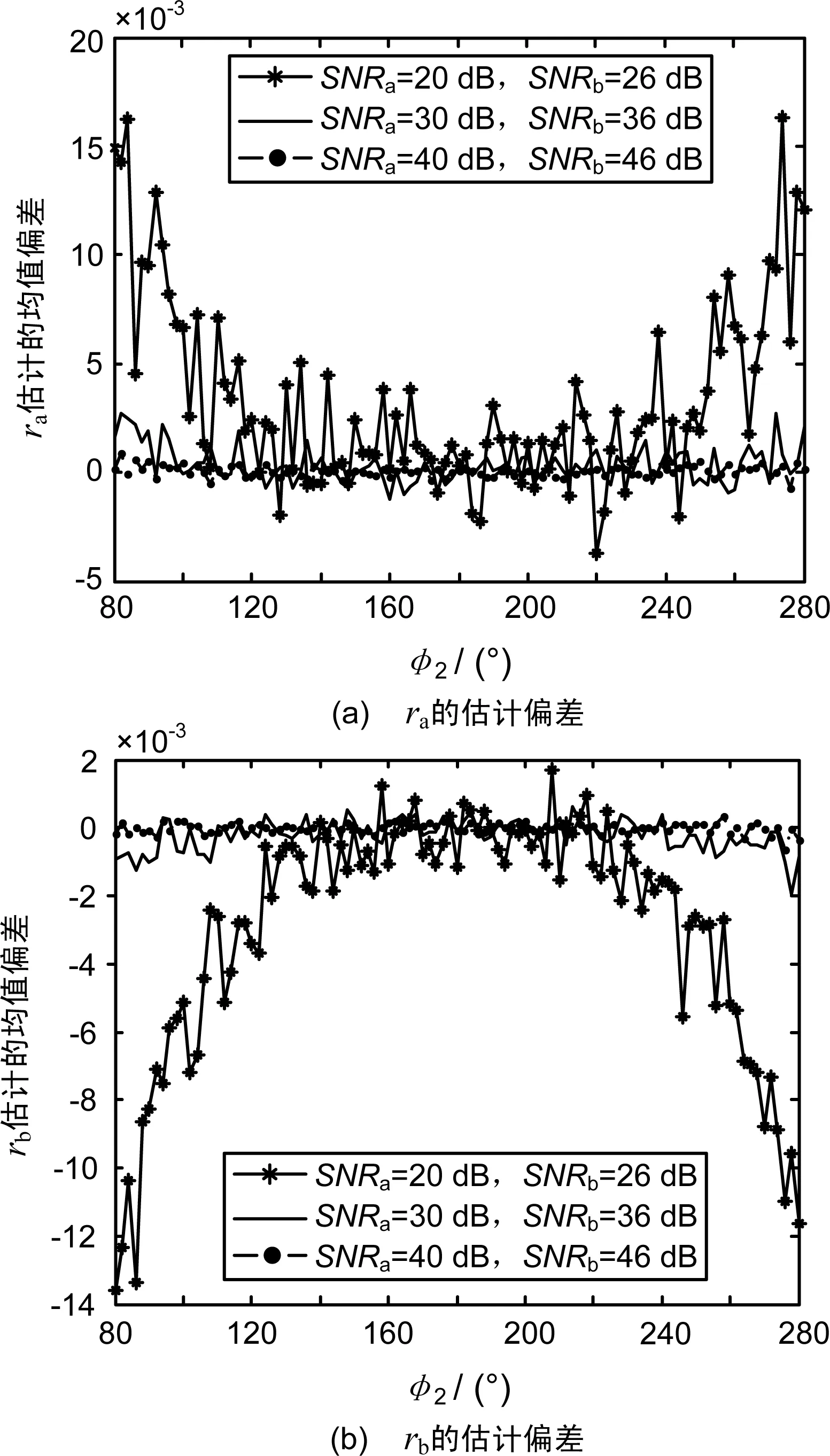
图1 ra和rb估估计偏差

图2 ra和rb估计的均方根误差

从图1可以看出，算法对单脉冲比的估计是存在一定偏差的，但总体而言偏差不大。对于给定的信噪比，当φ2接近180°时，cosφ1-cosφ2最大，算法性能最好。此时得到的均方根误差小于单目标情况下传统单脉冲比方法得到的结果(当信噪比为20 dB、30 dB和40 dB时，传统单脉冲比方法得到的均方根误差分别为0.073、0.023和0.007；当信噪比为26 dB、36 dB和46 dB时，传统单脉冲比方法得到的均方根误差分别为0.036、0.011和0.003 6)。当φ2接近80°或280°时，该算法得到的均方根误差仅为传统单脉冲比方法的2倍左右。

从图2还可以看出，仿真中得到的单脉冲比测量方差与理论分析基本一致。但在低信噪比条件下，仿真结果与理论值存在一定的偏差，这可能是由于在测量方差的分析中仅采用了一阶泰勒级数进行近似。

3.2 目标幅度起伏对算法性能的影响

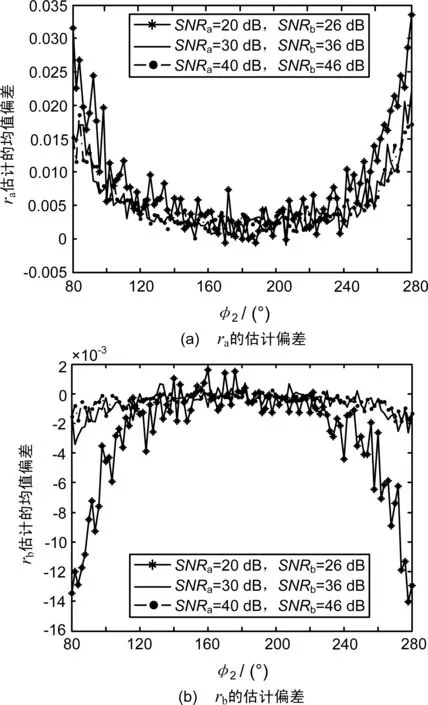
图3 目标起伏情况下的估计偏差

虽然相比于目标非起伏的情况，此时的估计偏差和均方根误差均有所增大，但是该方法仍然可以对两目标进行分辨。

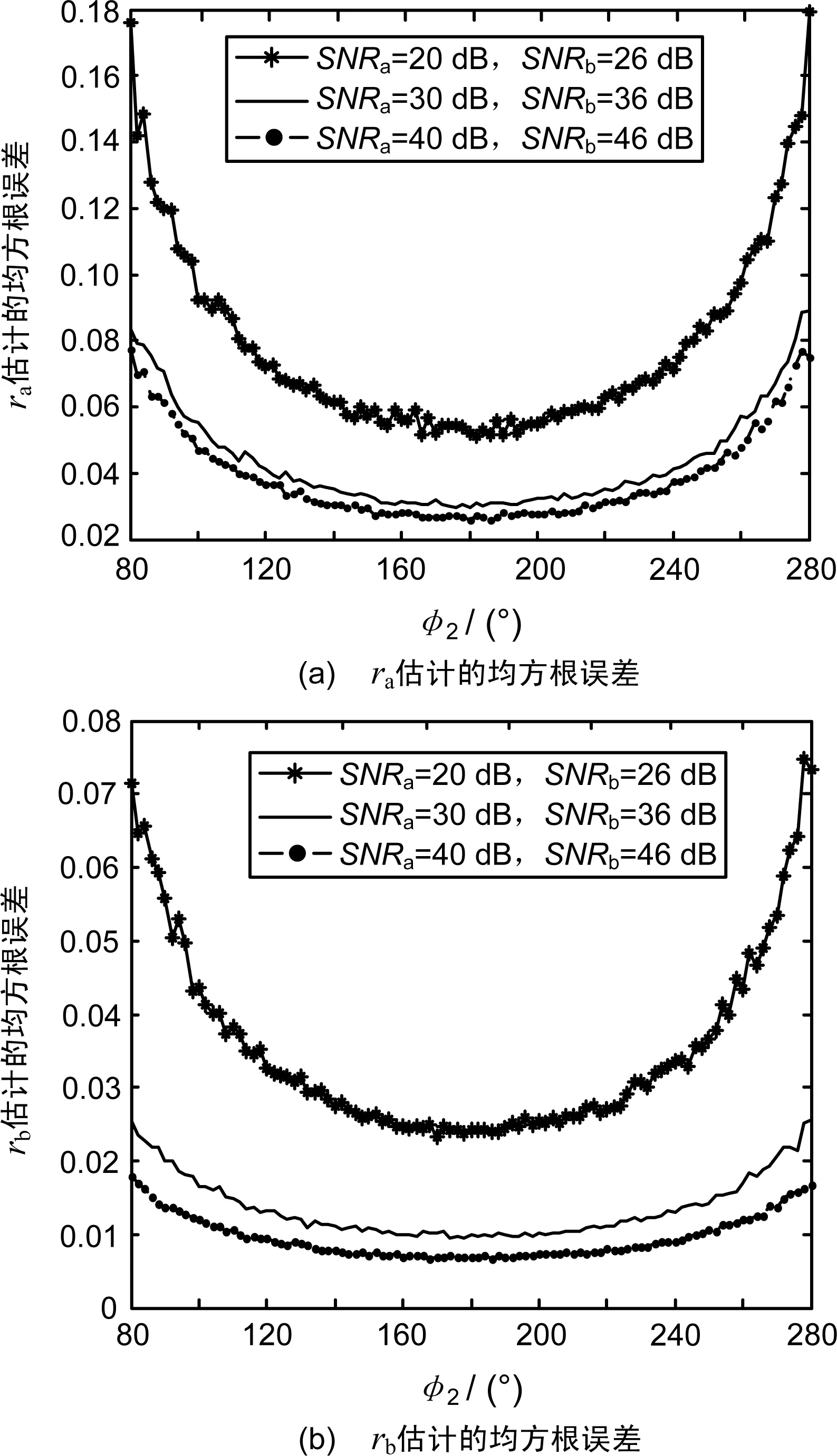
图4 目标起伏情况下的均方根误差

4 结束语

相控阵雷达中采用自适应单脉冲技术实现目标角度测量及副瓣干扰抑制，对于常用的自适应和差波束加权，证明了自适应单脉冲比的实数性质。雷达主瓣中存在2个不可分辨稳定目标情况下，利用2个时刻的和差通道信息得到了目标角度估计值。分析表明，角度估计的方差反比于目标信噪比以及两脉冲时刻接收信号的功率差。通过仿真对算法性能进行了验证，分析了角度估计偏差、方差以及目标起伏带来的影响。

[1] 郭崇贤.相控阵雷达接收技术[M].北京：国防工业出版社,2009.

[2] 张喜明,李秀成,张鹏.单通道单脉冲自跟踪信号源的设计[J].无线电工程,2014,44(2):24-56.

[3] LIE J P,SER W,SEEM C M S.Adaptive Uncertainty Based Iterative Robust Capon Beamformer Using Steering Vector Mismatch Estimation[J].Transactions on Signal Processing,2011,59(9):4 483-4 488.

[4] YU K,MURROW D J.Adaptive Digital Beamforming for Angle Estimation in Jamming[J].IEEE Transactions on Aerospace and Electronic Systems,2001,37(2):508-523.

[5] NICKEL U.Monopulse Estimation with Adaptive Arrays[J].IEE Proceedings-F,1993,140(5):303-308.

[6] NICKELU.Performance of Corrected Adaptive Monopulse Estimation[J].IEE Proceedings-Radar Sonar and Navigation,1999,146(1):17-24.

[7] KANTER I.Varieties of Average Monopulse Responses to Multiple Targets[J].IEEE Transactions on Aerospace and Electronic Systems,1981,17:25-28.

[8] BLAIR W D,BRANDT-PEARCE M.Monopulse DOA Estimation of Two Unresolved Rayleigh Targets[J].IEEE Transactions on Aerospace and Electronic Systems,2001,37(2):452-469.

[9] WANG Z,SINHA A,PETER W,et al.Angle Estimation for Two Unresolved Targets with Monopulse Radar[J].IEEE Transactions on Aerospace and Electronic Systems.2004,40(3):998-1019.

[10] 高明哲，祝明波，邹建武.基于改进粒子群算法的单脉冲雷达多目标分辨[J].无线电工程,2014,44(6):25-28.

[11] ZHENG Y,TSENG S M,YU K B.Closed-form Four-channel Monopulse Two-target Resolution[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(3):1 083-1 089.

[12] LUZhenxing,GAO Meiguo,JIANG Haiqing,et al.Closed-form Solutions for Directions of Two Steady Targets with Two Pulses in Monopulse Radar[C].2012 IEEE Radar Conference,Atlanta,GA,USA,2012:74-78.

[13] 杨荣山,张宁,张玉.基于L型阵的ESPRIT算法在DOA估计中的应用[J].无线电通信技术,2013,39(4):85-88.

[14] 刘柯邑,崔霞霞.一种改进的快速高分辨DOA估计方法[J].无线电通信技术,2009,35(4):41-43.

[15] 宋树田,秦建存.一种快速DOA估计算法[J].无线电通信技术,2009,35(5):58-61.

[16] 王永良,陈辉,彭应宁,等.空间谱估计理论与算法[M].北京:清华大学出版社,2004.

[17] NICKEL U.Overview of Generalized Monopulse Estimation[J].IEEE AES Magazine,2006,21(6):27-56.

[18] 王永良,丁前军,李荣锋.自适应阵列处理[M].北京:清华大学出版社,2009.

[19] 张贤达.矩阵分析与应用[M].北京：清华大学出版社,2004.

[20] MANOLAKIS D G,INGLE V K,KOGON S M.统计与自适应信号处理[M].周正,译.北京:电子工业出版社,2003.

A Two-target Resolution Technique with Adaptive Monopulse Based on Uniform Linear Array

LIU Er-ping1,LU Zhen-xing2

(1.AviationMilitaryRepresentativeOfficeofPLANavyStationedinBaodingRegion,BaodingHebei071000,China;2.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)

The adaptive monopulse is a widely used angular measurement method for phased array tracking radar in the presence of sidelobe jamming.This paper analyzes the basic adaptive sum and difference beamforming method for uniform linear array and proves that the adaptive monopulse ratio is a real value.An angular measurement method based on dual samples is proposed based on real adaptive monopulse ratio for two targets existing in radar main lobe,and the measurement error of monopulse ratio is analyzed.The simulation results show that,the proposed method can be used to estimate the angles of two unresolable targets and the estimation accuracy varies with the phase difference in the two samples.

adaptive monopulse;uniform linear array;unresolvable targets;angle estimation

10.3969/j.issn.1003-3106.2017.07.06

刘二平,鲁振兴.基于均匀线阵的自适应单脉冲两目标分辨技术[J].无线电工程,2017,47(7):25-29.[LIU Erping,LU Zhenxing.A Two-target Resolution Technique with Adaptive Monopulse Based on Uniform Linear Array[J].Radio Engineering,2017,47(7):25-29.]

2017-04-08

海洋公益性行业科研专项基金资助项目(201505002)。

TN958.92

A

1003-3106(2017)07-0025-05

刘二平 男，(1977—)，工程师。主要研究方向：自动化技术、信号处理算法。

鲁振兴 男，(1984—)，工程师。主要研究方向：雷达信号处理。