基于多项式插值的外测数据拼帧及平滑问题研究
淡 鹏,王 丹
(1.宇航动力学国家重点实验室,陕西 西安 710043;2.西安卫星测控中心,陕西 西安 710043)
基于多项式插值的外测数据拼帧及平滑问题研究
淡 鹏1,2,王 丹1
(1.宇航动力学国家重点实验室,陕西 西安 710043;2.西安卫星测控中心,陕西 西安 710043)
针对微波统一测控系统外测测量数据的插值对齐、拼帧与平滑计算问题,结合工程实际情况,探讨了基于多项式模型的计算方法,给出了多项式的选取建议,以及测角等类型测元数据处理的较高精度计算方法。仿真计算结果表明提出的方法可行,不同的插值方法、多项式选取和角度处理方法等对精度有较大影响,在具体的计算中需要综合考虑精度及实时性要求的限制。研究结果对外测测量数据的处理有一定的参考价值。
统一测控系统;插值;测距;测角
0 引言
航天器跟踪测量中,微波[1]统一测控系统[2]外测[3]测量数据是一类重要的观测数据,在卫星轨道、火箭弹道和返回舱弹道等的计算中有着重要价值。但由于测量机理及设备采集方法等方面的原因,此类设备的外测测距[4]、测速[5]和测角[6](包括方位角和仰角)等测元信息在实际采集后的传输中常常不在一帧数据中存在,从而给需要同时使用其中几类数据的计算带来困难,如某些实时弹道[7]计算方法需要使用测距、测角均有的数据,这时就需要对其中几类或全部测元数据进行拼帧操作,使之成为测元“完备”[8]的观测数据。但这些测元的时标[9]在修正后或修正前就可能不一致,从而需要对其进行基于时标的插值操作。另外,在数据采集频率较大时(如20点/s),为减少数据量,有时还需对多点数据进行平滑[10]处理,这些问题从本质上来说涉及的是对这些测元数据的插值及拟合问题。
目前对外测数据不同测元进行拼帧及平滑问题进行深入研究的文献较难找到,大多是直接使用其数据的应用算法(如文献[4-5,11-12])。为此,本文从工程实际情况出发,在充分考虑工程计算面临的实际困难,以及精度和可靠性要求的情况下,采用多项式[13]插值的方法对外测数据拼帧与平滑问题进行了分析。
1 外测数据多项式插值及平滑算法
对外测数据的拼帧及平滑问题,通过实际的工程计算可以发现,不合理的插值算法可能使得拼接后的数据计算的弹道偏差增大。特别是在测站对航天器的跟踪仰角出现最大值的前后(称为“过顶”,如图1所示),此时角度测量量变化快、精度低的插值计算会使得角度误差增大,进而使得单点测距与角度数据转换为位置时误差变大。同时考虑到在实时的外测数据处理中,过于复杂的插值算法又较难使用。为此具体的实现中要兼顾可靠性、精度和实时性等多个要求。
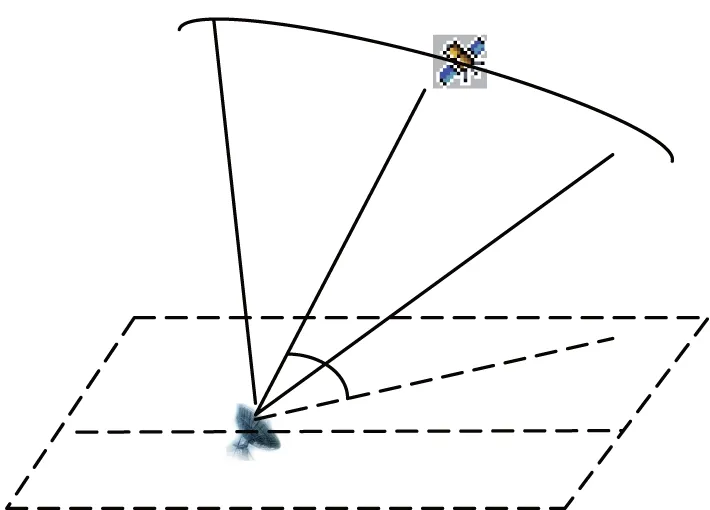
图1 航天器仰角“过顶”示意
1.1 多项式插值及拼帧方法
对外测数据中不同测量元素数据的插值与拼帧、平滑操作的基本算法是曲线拟合与插值,这方面的方法很多,如较常用的拉格朗日插值[13]、最小二乘曲线拟合插值[14]、样条插值[13]和抛物线插值[13]等。其中,拉格朗日插值具有算法简单、实现容易的特点,而最小二乘[15]曲线拟合插值在消除野值方面具有较好表现。为此本文在多项式插值与拟合计算中,主要采用了拉格朗日与最小二乘曲线拟合2种方法,相关方法实现可参考文献[13]。
当测距、测角和测速等测元数据插值到同一时间点后,即可按时间基准进行拼帧操作。在插值及拼帧操作中需要注意以下方面:
① 时标的跨天处理。在外测测元数列插值中,需要解决的一个问题是时标的跨天问题。处理方法为:对一时间点为T1,T2,…,Tn的测量序列,插值计算TK处的值,可将其时间点转换为T1-TK,T2-TK,…,Tn-TK,这样只需插值T=0处结果。此处通过对时间做差,避免了跨天问题。
② 插值中的时标对齐策略。在不同测元数据对齐时,可采用2种插值策略:一是对每一个测量量都进行插值,然后以时间驱动查找相同的时标点进行拼接;二是以某一个测量量时标为基准,将其他测量量插值到此时标处,这样可减小某一维数据的插值误差。如可采用以测距数据时标为基准,将测角、测速插值到其时标处然后进行拼接。
1.2 计算中的角度数据处理
角度数据是外测数据插值与平滑计算中需要特别对待的一类。此类数据在数值上可能是不连续的,如方位角的“过北”现象(从360°变为0°或相反过程),且插值精度低时会使误差变大。为此给出下面的转换插值算法。
① 对仰角E:若直接对角度进行插值拟合则偏差太大,故改为E的函数f(E)进行插值计算(f(E)通常取为正弦函数),最后再解算出E。
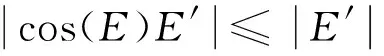
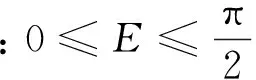
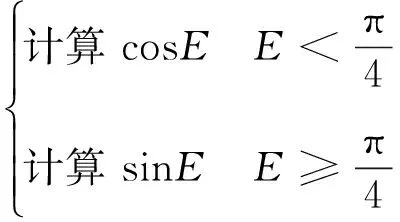
此时,函数f(E)变化率相对较小,一定程度上可减小插值误差。
② 对方位角A:在方位角“过北”情况下(即方位角从第1像限进入第4像限、或者从第4像限进入第1像限时),插值计算时需要进行角度连续性判断,判断方法为,如果前后两点方位角满足|Ak-1-Ak|>180.0,则认为过北。
为简化计算并正确处理过北情况,对A的处理可采用以下2种方法:
方法1:采用三角函数法进行插值计算,具体为对正弦与余弦函数sin(A)、cos(A)分别进行插值计算,然后再借用反三角函数arctan2解算出A。

关于角度与三角函数插值的误差问题,通过对某任务某观测站过顶前后的实测跟踪数据分别采用角度直接插值以及三角函数插值2种方法计算,然后做差,得到的差值曲线如图2所示。
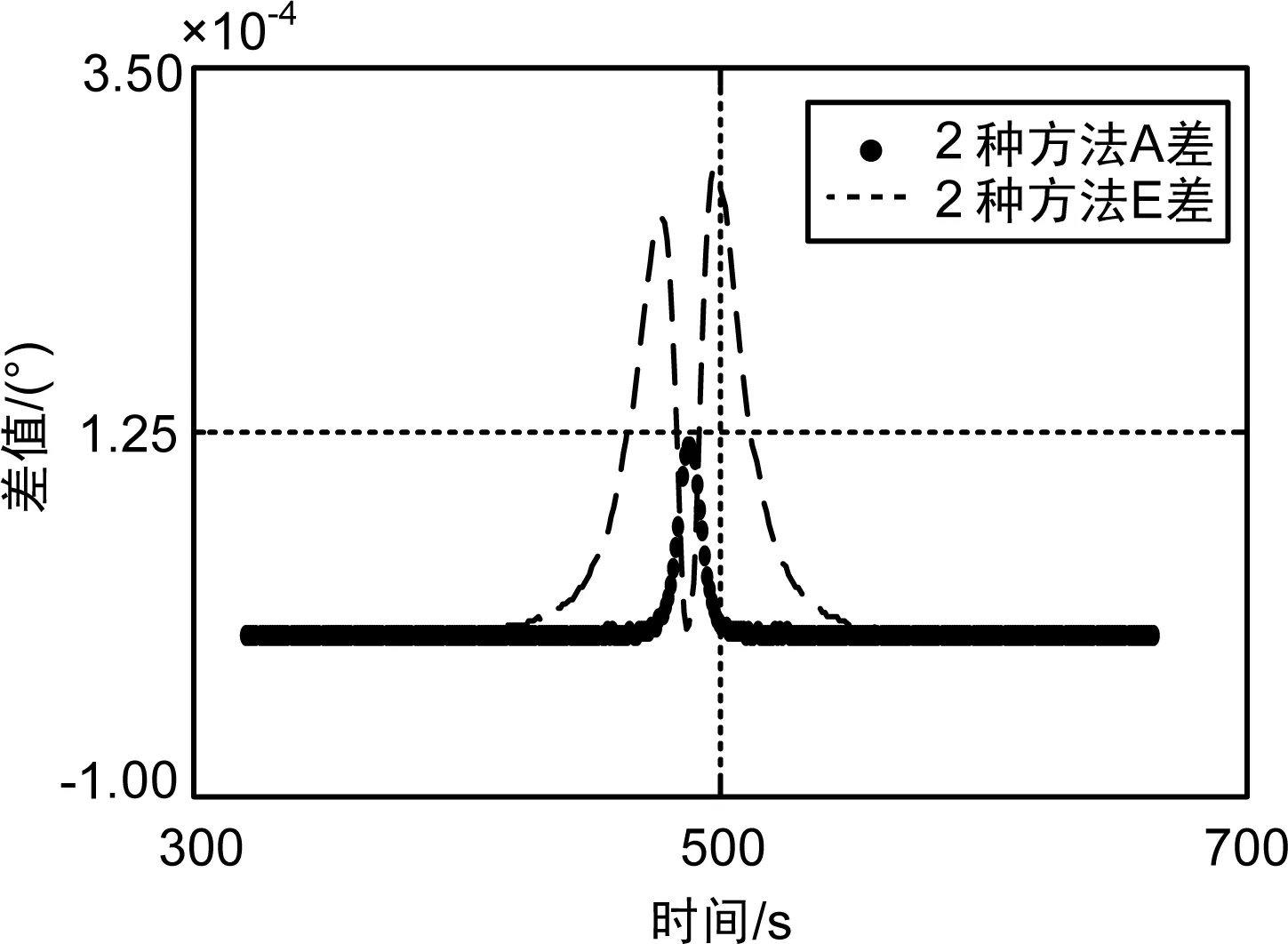
图2 测角数据2种方法插值结果互差散点
从图2中可看出,此样本数据2种方法计算结果,方位角最大差值为0.000 115°,仰角最大差值为0.000 283°,并且仰角偏差大的地方出现在其变化率大的地方,2种方法计算结果差别很小。
考虑到航天器飞行过程是位置、速度连续变化的过程,对TK处外测观测量的插值最终要归结为TK处飞行状态量的插值。因此也可从二者之间的转换关系比较直接使用角度与使用三角函数时的精度。
对测站地平坐标系[4]的球坐标观测量ρk,Ak,Ek和目标在地心固连坐标系[5]的坐标可表示为
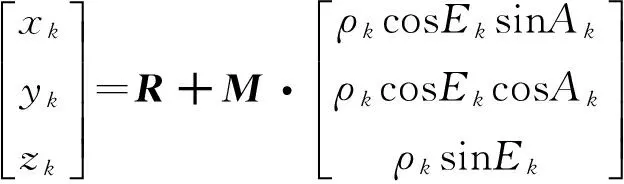
(1)
式中,M为测站地平系到地心固连系的转换矩阵;R为测站在地心固连系下的坐标。当测站确定时,M与R为确定量,而测距ρk的插值结果一定情况下,位置的插值精度直接决定于测角三角函数的插值精度。
1.3 多项式平滑算法
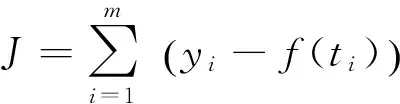
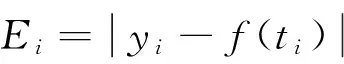
2 仿真计算与分析
为验证算法有效性及对不同条件下的计算效果进行对比,给定一组轨道初值,外推计算出某测站在过顶前后非整秒点的理论测量值进行曲线拟合插值计算。
考虑到在实时工程计算中,对数据处理时延要求严格,为此在时标插值计算中最多使用插值点后1 s内的数据进行计算。
2.1 拉格朗日插值测试
仿真数据为1 点/s,作以下2种计算:
算例1:采用拉格朗日插值方法,使用了插值点后的1点数据(即进行内插),分别计算了总点数为2点、3点和4点拟合结果,并与理论测量值做差。
算例2:只使用插值点时间之前的数据(即进行外插),外插后1 s的数据,分别计算了总点数为2点、3点和4点计算结果,并与理论测量值做差。
计算结果如图3所示。需要说明的是,外插时2点计算结果中某些值超出范围,未能在图中显示出来。
从图3中可以看出,对于内插,3点与4点插值误差明显小于2点插值结果,而4点插值结果误差已经很小,若采用更多点插值,误差并没有太多提高,相反使用过多点还可能使结果出现病态。而对于外插,4点插值结果要好于3点,而3点又明显好于2点结果。总体来说,内插好于外插。
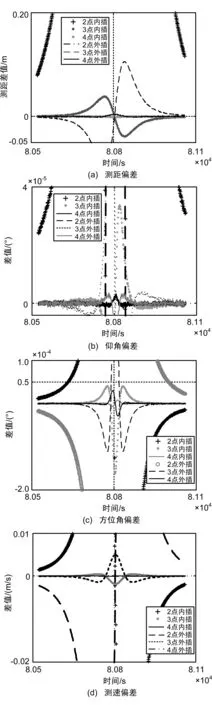
图3 拉格朗日插值对比
2.2 最小二乘拟合插值测试
仿真1 点/s的数据,分别使用10点、7点数据做2次和3次多项式最小二乘拟合插值(内插前1 s的数据),然后将插值结果与理论值做差,所得差值曲线如图4所示。

图4 最小二乘插值对比
从图4中可以看出,3次多项式最小二乘插值效果要好于2次多项式。而10点数据最小二乘插值结果并不比7点好,这是因为点数太多时,使用的插值点时标之前的数据过多(出于实时计算时延考虑,此处只使用了目标插值点后1 s的数据,其余均为之前的数据),使得拟合值对前面点的方差更小,曲线更趋近于前面的点。
2.3 多项式最小二乘平滑测试
仿真20 点/s数据,采用每2 s数据进行多项式中心最小二乘平滑计算,平滑后数据与理论计算值做差,可得到测距差在1 cm范围内,测角差在1″范围内,满足计算的精度要求。
2.4 结论
从上面的仿真计算可得出如下结论:
① 本文给出的基于多项式的外测数据插值与平滑算法是有效的,通过三角函数来实现角度数据的插值,可有效避免直接使用角度造成的不连续问题;
② 在外测数据插值计算时,推荐使用3次多项式插值,当采用拉格朗日插值算法时,可使用4点公式计算(即3次多项式);
③ 多项式最小二乘法的插值对齐与平滑算法对野值的剔除有一定效果,但使用时应尽量进行内插,外插时精度降低较大。
同时应该看到,拟合结果除了与使用点数、拟合方法有关外,还与数据的变化率和插值位置等因素有关,因此上面给出的结果只是针对于给定的计算条件。
综合对比图3和图4可以发现,最小二乘曲线拟合插值结果误差并不一定比拉格朗日结果好,在实时外测数据处理中,使用拉格朗日插值已经能够满足精度要求。但是考虑到观测值的野值问题,在数据质量不好的情况下使用最小二乘拟合方法结果可能会好一些。
3 结束语
本文对基于多项式算法的外测数据插值、拼帧及平滑方法进行了探讨,对计算中的有关细节问题进行了分析,计算结果表明了本文算法的有效性。
应该看到,在实际工程计算中,外测数据实时拼帧处理中的插值对齐问题需要综合考虑时延要求和插值位置等因素。综合上面的计算结果,认为实时插值时使用的点数不宜太多,应尽量避免外插的发生(但会增大计算延迟),同时简单的拉格朗日插值在精度上可以满足与最小二乘相当的精度(数据质量不好时差些,但这可通过在具体的数据使用过程中,应用滤波等方法进行二次处理来解决)。下一步将重点在测量数据的滤波处理等方面进行研究。
[1] ZAKA I,REHMAN H U,SHAH S I.PSO- and GA-based Jammer Excision in CDMA[J].Journal of Circuits Systems and Computers,2010,19(1):123-138.
[2] 赵楠.统一扩频测控系统中关键技术研究[D].哈尔滨:哈尔滨工业大学,2011.
[3] 茅永兴,马静远,钟德安,等.基于速度增量修正的卫星入轨段外测数据定轨新方法[J].宇航学报,2016,37(9):1 049-1 055.
[4] 淡鹏,李恒年,李志军.应用三向测量数据的深空探测器实时滤波定位算法[J].航天器工程,2015,24(2):21-26.
[5] 淡鹏,李恒年,张智斌.一种火箭外测弹道实时重建的自适应滤波算法[J].弹箭与制导学报,2013,33(6):188-190.
[6] 王英玲.低仰角跟踪技术研究及应用[J].无线电工程,2008,38(9):43-46.
[7] 胡亚男,甘友谊,王盛玺.卫星发射任务主动段实时弹道算法研究[J].无线电工程,2013,43(4):28-31.
[8] 淡鹏,李恒年,张定波,等.基于多元非完备信息的实时滤波定轨方法[J].飞行力学,2014,32(3):283-288.
[9] 王金华,刘魁星,韦欣荣.基于矩阵构造的伪码测距时标偏差标定方法[J].无线电工程,2016,46(12):47-50.[10] 梁健,王京京.基于改进Kalman滤波算法的航迹平滑[J].无线电工程,2015,45(5):20-23.
[11] 张艳,郭军海,慈颖.基于动力学约束的实时弹道滑动处理方法[J].飞行器测控学报,2011,30(3):56-60.
[12] 雷鸣,张玉如.自适应滤波方法在外弹道实时测量中的应用[J].舰船电子工程,2002(3):18-24.
[13] 石瑞民.数值计算[M].北京:高等教育出版社,2004.
[14] 王易南,闫杰,温琦.基于最小二乘的航天器天文导航定姿算法研究[J].电子设计工程,2014,23(5):58-59.
[15] 米芳彬,徐小刚,梁健.基于有限元记忆最小二乘的雷达误差配准算法[J].无线电工程,2016,46(2):65-68.
[16] 刘玉明,张宝华.一类FIR滤波器的加权最小方差设计[J].无线电工程,2000,30(4):52-54.
Discussion on Tracking Data Completing & Smoothing Using Polynomial Interpolation
DAN Peng1,2,WANG Dan1
(1.StateKeyLaboratoryofAstronauticDynamics,Xi’anShaanxi710043,China;2.Xi’anSatelliteControlCenter,Xi’anShaanxi710043,China)
For tracking data interpolation,completing and smoothing of microwave unified TT&C system,a polynomial calculation method is discussed,some suggestions for the selection of polynomial formula as well as some high-precision processing method for bearing measurement are provided.The simulation results show that the method given in this paper is feasible,and different formulas,interpolation methods and bearing processing methods will result in apparent accuracy deviation.In practical engineering calculation,the result precision and real-time requirement,etc.need to be considered in the processing of tracking data.The results provide a reference for the processing of external tracking data.
unified TT&C system;interpolation;ranging;bearing measurement
10.3969/j.issn.1003-3106.2017.07.05
淡鹏,王丹.基于多项式插值的外测数据拼帧及平滑问题研究[J].无线电工程,2017,47(7):20-24.[DAN Peng,WANG Dan.Discussion on Tracking Data Completing & Smoothing Using Polynomial Interpolation[J].Radio Engineering,2017,47(7):20-24.]
2017-01-10
国家自然科学基金资助项目(61302098)。
V412.4
A
1003-3106(2017)07-0020-05
淡 鹏 男,(1979—),硕士,工程师。主要研究方向:航天器数据处理技术。
王 丹 女,(1980—),硕士,工程师。主要研究方向:航天器数据处理技术。

