欠饱和状态下基于流量的动态交通路段行程时间算法

钟会玲

(浙江浙大中控信息技术有限公司，浙江杭州310053)

欠饱和状态下基于流量的动态交通路段行程时间算法

钟会玲

(浙江浙大中控信息技术有限公司，浙江杭州310053)

通过深入分析欠饱和状态下的路段中间地点速度，提出Webster与基于流量的动态交通路段行程时间算法，利用Webster模型得出路段直行红灯延误时间，引入流量作为通畅状态下行驶时间和红灯延误时间比重参数，且路段直行通畅状态下行驶时间比重参数与流量负相关，红灯延误时间比重参数与流量正相关，比重参数通过路段直行真实行程时间与模拟行程时间回归分析得出。以2016年浙江省海宁市微波及线圈数据为研究对象，结合交叉口红绿灯配时，首先清洗微波和线圈数据，然后利用Webster与基于流量的动态交通路段行程时间算法，结合回归分析训练集得出的路段行程时间关系式，最后利用测试集，得出路段行程时间与真实路段行程时间显著性水平为0.684，并且与固定参数的路段行程时间相比，显著性水平高出0.143，可见该组合算法具有较好的准确率和实用性。

交通流;行程时间;Webster;线性相关

1 方法与数据

1.1 方法

(1)Webster延迟模型

计算路口各个进口方向上在采样周期内的车辆延误。计算交叉口给定车道的车辆平均延误的Webster公式如下所示

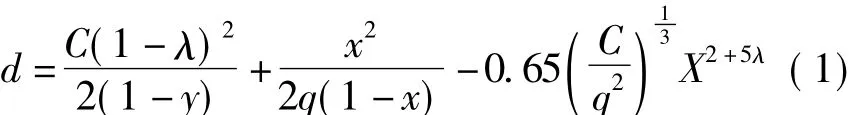
式中:d为每辆车的控制延误，s/辆;C为交叉口周期，s;λ为绿信比为车道的绿灯时间，s;q为流量×3 600，Q为采样周期内车辆数，辆/采样周期;y为流量比，s为路口进口一条车道的饱和流率，辆/h;x为车道的饱和度

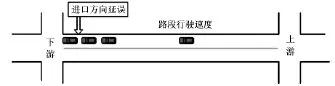
图1 进口方向延误

若路口某进口方向有n条车道采样数据的流量分别为q1，…，qn，则分别计算n个车道的平均延误d1，…，dn，然后按下式求得该进口方向上的平均控制延误和总流量分别为

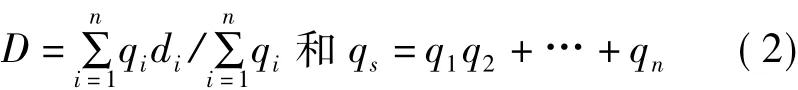
若发布间隔横跨M个信号控制周期结束点，这M个控制周期内该进口方向的延误分别为D1，…，DM，总流量分别为qs1，…，qsM，则发布间隔内的该进口方向上的平均延误为

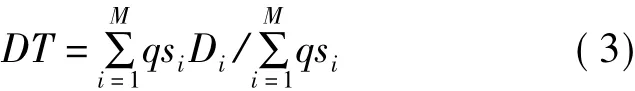
若发布间隔内无信号控制周期结束点，即M= 0，则利用上一发布间隔内的该进口方向上的延误时间作为本次发布间隔内的延误时间。

(2)线性回归模型

回归分析是研究随机变量之间的相关关系的一种统计方法，其用意是研究一个被解释变量(又称因变量)与一个或多个解释变量(又称自变量)之间的统计关系。

论文利用的模型为多元线性回归，将所选变量全部强行进入回归，其线性模型即

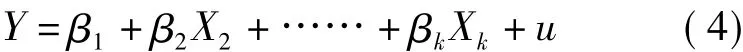
论文通过利用Webster模型得出路段直行红灯延误时间，引入基于流量的动态交通路段行程时间算法，结合回归分析得出路段行程时间与红灯延误时间、地点速度以及路段交通流量间关系。并利用测试集验证结果，得出较高的线性相关度，表明该模型算法适用于城市交通路段行程时间计算。

(3)相关分析

相关分析是研究两数值型变量线性相关性的常用方法，需经过以下两个步骤:第一，计算Pearson样本相关系数r;第二，对样本来自的两总体是否存在显著线性关系进行检验。

Pearson样本相关系数即样本简单相关系数，反映变量间线性相关程度的强弱;对样本来自的两总体是否存在显著线性关系进行检验，首先假设两总体零线性相关，其次计算Pearson相关系数的检验统计量t及其对应的概率P，最后比较P与显著性水平通常设为0.05得出是否线性相关结果。

1.2 数据

为了验证所提方法的有效性，以2016年3月份浙江省海宁市水月亭路上海昌路至文苑路交通流数据为研究对象，该路段上下游路口现安装有电子警察设备，电警数据包括车辆信息，车辆经过地点、方向，车道号及经过时间，利用该每5分钟数据形成车辆经过某路段数据，并通过删除滞留车辆数据，绕弯车辆数据达到清洗数据的目的，最后得出每5分钟路段真实行程车速。路段上下游路口信号配时数据，中间装有微波设备，通过微波数据清洗规则达到清洗异常数据的目的。

1.3 实验流程

原始电警数据经过处理后形成路段过车数据，清洗干净后计算出路段真实行程车速，由于海宁即使是早晚高峰交通流也处于欠饱和状态，可将微波地点速度作为路段畅行车速，进而得出畅行时长，由Webster模型得出路段的延误时长数据，Webster与基于流量的动态交通路段行程时间算法的具体实验流程如图2所示，包括5个步骤:

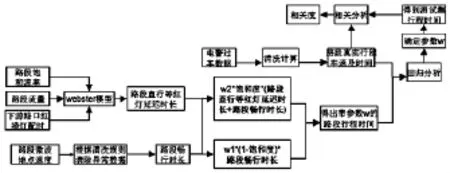
图2 欠饱和状态下基于流量的动态交通路段行程时间算法实验流程

步骤一:原始电警数据经过处理后形成路段过车数据，清洗干净后计算出路段真实行程车速及行程时间。

步骤二:原始微波地点数据经过排除异常数据，清洗干净后计算出路段畅行车速及对应畅行时长。

步骤三:利用路段饱和流率、路段实时流量、路段下游路口配时信息数据，通过Webster模型得出路段直行等红灯延迟时长。

步骤四:利用步骤二步骤三结果，并且引入路段直行流量占路段饱和流率比重作为动态参数组成之一，剩余参数由w替代。

步骤五:利用步骤四结果得到带参数w的路段行程时间。

步骤六:根据步骤一的路段真实行程时间与步骤五的带参数路段行程时间，通过回归分析确定参数w。

步骤七:将参数w带入测试集中，得到测试集的行程时间，与路段真实行程时间进行相关分析，如果得到显著性水平大于0.5，表明该组合算法具有较好的准确率和实用性。

2 结果

2.1 电警路段行程车速

论文以2016年3月水月亭路上海昌路至文苑路交通流数据为研究对象，分析交通路段速度一个月每天每5分钟的时间分布特性。选取具体3月1号的交通路段速度的时间分布特性如图3所示，由图3可以看出，在7:00－9:00的时段内水月亭某一路段交通路段速度相对较低，呈现出早晚高峰的特征。

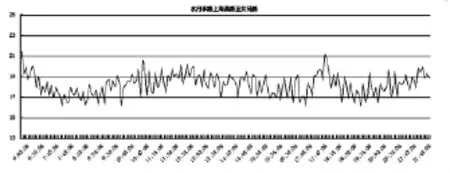
图33 月1号水月亭路上海昌路至文苑路路段真实行程车速

2.2 线圈数据地点速度对应畅行时间及延误时间

根据表1清洗规则，清洗微波或线圈异常数据，每条路段交通流参数的合理区间都可能不同，因此需根据道路实际环境进行设置。

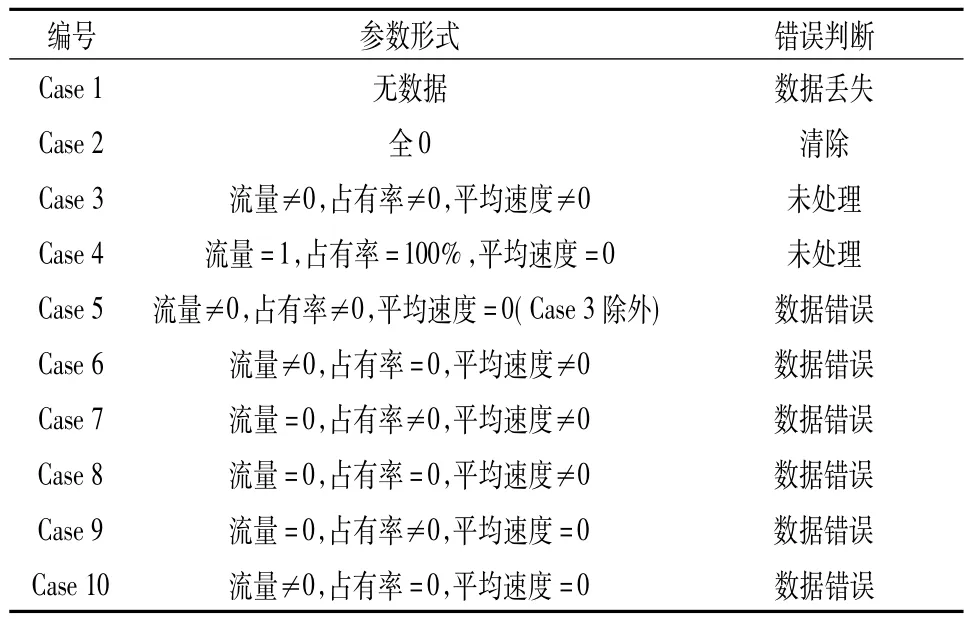
表1 交通流参数错误组合

清洗后根据流量加强平均得到路段畅行车速，3月1号水月亭路上海昌路至文苑路路段中间地点车速如图4。

在该发布间隔内基于该种检测器的路段畅行行驶时间为

根据Webster模型即公式一、公式二和公式三得出发布间隔每5 min的该进口方向上的平均延误DT，引入路段直行流量占路段饱和流率比重作为动态参数组成之一

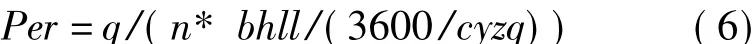
其中，bhll为饱和流率单位秒，cyzq为采样周期，微波为60 s，线圈为30 s，q为采样周期内的路段流量，n为该出口方向加入计算的车道数。

发布间隔内基于该种检测器的带参数的路段行程时间ts:

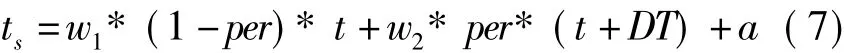
模拟路段行程速度

式中:w1，w2为权重参数，a为常量。

图43 月1号水月亭路上海昌路至文苑路路段中间地点车速

2.4 确定基于流量的动态参数

在上一步得出的带参数路段行程时间的基础上，结合路段真实行程车速得出真实行程时间，再利用回归分析得出真实行程时间与基于流量的延误时间及畅行时间三者间关系，参数w1为0.004，w2为0.064，a为50.58，且显著性水平为0.864。将动态参数带入上一步中公式七和公式八，得出每5 min的模型得出的路段行程时间及速度。以2016年3月1号数据为训练集的一部分，模型得出的路段行程速度与真实路段行程车速对比图如图6。

2.5 验证结果

固定参数方法中通常将w2*per定为经验值0.05，w1*(1－per)定为0.95，根据公式七得出的路段行程时间与路段真实行程时间的线性相关的显著性水平为0.541，且平均绝对误差为20.17 s。固定参数的路段行程车速与真实路段行程车速对比图如图5。

将动态参数带入公式七和公式八，得出每5分钟的模型得出的路段行程时间及速度。以2016年3月2号数据为测试集，模型得出的路段行程时间与真实路段行程时间线性相关的显著性水平为0.684，且平均绝对误差为9.89 s，并且与固定参数Webster模型的路段行程时间相比，显著性水平高出0.143，平均绝对误差减少10.28，可见该组合算法具有较好的准确率和实用性，基于流量的动态交通路段行程车速与真实路段行程车速对比图如图6。

图5 固定参数的拟合路段行程车速与真实路段行程车速对比图

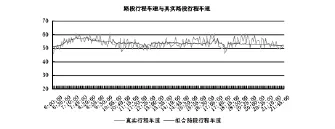
图6 动态参数的拟合路段行程车速与真实路段行程车速对比图

3 讨论

首先论文选择海宁交通数据为研究对象，由于海宁交通流包括早晚高峰期都处于欠饱和状态，路口车辆均能在一个灯次内通过，因此选择Webster模型为基础的研究模型较为合理。

其次论文为将模拟数据更接近真实结果，采用电警过车数据为路段真实行程车速依据，且电警过程数据清洗过程严格，尤其是车流量大的时候所得出的行程时间准确率可达到95%以上，可靠性高。

最后论文为通过地点车速数据与道路及信号配时信息数据推算出路段行程时间，在Webster模型的基础上引入流量作为通畅状态下行驶时间和红灯延误时间比重参数组成之一，以电警过车数据为基准，回归分析得出剩余组成参数值，相对于固定参数的通畅状态下行驶时间和红灯延误时间模型显著性水平高，说明欠饱和状态下，基于流量的动态交通路段行程时间算法准确率较高。并利用测试集验证基于流量的动态交通路段行程时间算法，说明模型选择合理。

4 结论

论文通过有效分析得出，路段的行程时间由路段信号配时信息、路段基础信息、路段通畅状态下行驶时间决定，在欠饱和状态下，以Webster模型为基础，引入流量作为通畅状态下行驶时间和红灯延误时间比重参数组成之一，结合由电警数据得出的路段真实行程车速及时间，利用回归分析得出基于流量的动态参数，拟合度高，说明模型选择合理。

论文用训练集得出模型，并用测试集验证模型，且验证结果的线性相关显著性水平偏高，平均相对误差偏低。并且相对于固定参数的通畅状态下行驶时间和红灯延误时间模型显著性水平高，能够提高交通状态判别的准确性。

［1］王志华，史天运.射频识别技术(RFID)在交通领域的应用现状［J］.交通运输系统工程与信息，2005，5(6): 96－99.

［2］刘阳，尹铁源，葛震，宋继红.数字图像处理应用于车辆牌照识别的研究［J］.辽宁大学学报(自然科学版)，2004，31(1):65－68.

［3］盖春英.区域公路网交通量实用预测方法研究［D］.哈尔滨:哈尔滨工业大学，2000.

U492

C

1008－3383(2017)04－0183－03

2016－06－08