采用Belikov列推和跨阶次递推方法计算超高阶缔合勒让德函数

欧阳明达，张敏利，于 亮

(1.地理信息工程国家重点实验室，陕西 西安 710054；2.西安测绘总站，陕西 西安 710054)

采用Belikov列推和跨阶次递推方法计算超高阶缔合勒让德函数

欧阳明达1，2，张敏利2，于 亮2

(1.地理信息工程国家重点实验室，陕西 西安 710054；2.西安测绘总站，陕西 西安 710054)

超高阶球谐重力场模型的精确构制与快速计算取决于缔合勒让德函数的计算方法。在前人研究的基础上，文中对适合超高阶缔合勒让德函数计算的Belikov列推和跨阶次递推方法进行介绍，为验证精度，通过两种途径对计算结果进行检验，并比较其计算速度。结果表明，采用两种算法得到的每个勒让德函数的绝对精度均优于10-12，在低阶，跨阶次递推方法的计算用时大约是Belikov列推法的2倍，随着阶数的升高，跨阶次递推算法表现出明显的速度优势。

勒让德函数；递推公式；球谐分析

随着地球重力场模型的不断精化，超高阶次缔合勒让德函数的计算已经成为了地球重力场和相关领域中的重要研究课题[1-8]。目前，递推计算方法包括：标准前向列推法、标准前向行推法、跨阶次递推法和Belikov列推法。王建强等对4种方法的计算程序做了改进，从计算速度、计算精度两方面分析比较了阶次高至3 060阶的各种方法的优劣[9]；刘缵武等研究发现，超过2 000阶次的缔合勒让德函数在接近两极时达到极大的数量级，导致现有递推方法在计算缔合勒让德函数值及其导数值时出现溢出，他提出通过插入压缩因子，修改递推算法，并结合使用Horner求和技术计算了球谐级数的部分和[7]; 于锦海等计算了超高阶次勒让德函数，对计算结果的精度进行了检核，使得可以在双精度数的范围内对任意阶次的勒让德函数进行计算[8]。

吴星等详细介绍了现有多种缔合勒让德函数的递推计算方法，通过数值试验证明，Belikov列推法和跨阶次递推法是计算超高阶次缔合勒让德函数较优的方法[6]。在此研究的基础上，本文采用两种途径对超高阶缔合勒让德函数计算方法的结果精度进行了检验，并比较了其计算速度。

1 缔合勒让德函数计算公式

勒让德函数，通常以符号pn(x)表示，n为阶数，它满足于勒让德微分方程

(1)

1.1 跨阶数递推公式

(2)

其中

(3)

即可以写成

(4)

(5)

当m≥2时，有公式

(6)

其中

(7)

(8)

(9)

(10)

1.2Belikov列推公式

Belikov列推法引入新的非正常化球谐函数

(11)

pnm(cosθ)是非正常化的勒让德函数，可以得到其递推关系为

(12)

(13)

由式(11)和式(13)可得

(14)

其中

(15)

2 结果精度分析与比较

引入检核公式[10]，对其精度进行评估。

(16)

式(16)能够用于评价某个特定阶次勒让德函数的计算精度，最高阶数取N=3 000，考虑到θ值在接近于两极附近时会出现溢出，令θ=3°,30°,60°,87°，图1和图2分别给出了采用跨阶次递推法和Belikov递推法得到的Tn结果的统计图。可知，两种递推方法的计算结果精度均优于10-13，跨阶次递推法的相对精度值震荡曲线较为剧烈，角度越小，振幅越大，在θ<30°左右的范围，阶数在N=500阶内，相对精度不断提升，当N>500阶，相对精度呈下降趋势，当θ<30°时，阶数越高，相对精度越低。随着阶数的升高，Belikov递推法的相对精度不断降低，且震荡曲线较为平滑。

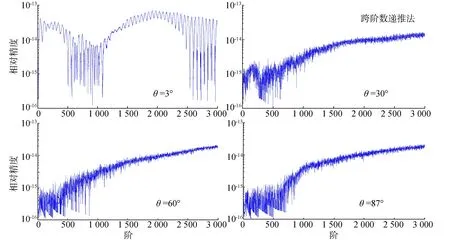
图1 当θ=3°,30°,60°,87°时，跨阶次递推法Tn结果统计图

图2 当θ=3°,30°,60°,87°时，Belikov递推法Tn结果统计图

式(16)并不能用来评价同一阶数内勒让德函数值平方和的精度，为此，引入另一个检核公式[11]

(17)

图3 当N=90,360,1 000,1 600,2 160时，跨阶次递推法η(θ)的对数值曲线

图4 当N=90,360,1 000,1 600,2 160时，Belikov递推法η(θ)的对数值曲线

利用缔合勒让德函数计算地球重力场模型要求在保证精度的情况下，尽可能实现快速计算。表1给出了在同一台计算机上采用跨阶数递推法和Belikov递推法计算不同阶数缔合勒让德函数从θ=1°至θ=89°的时间，可以看出，在低阶，跨阶数递推算法的计算时间大概是Belikov递推算法的2～3倍，随着阶数升高，Belikov递推算法的耗时性逐渐体现，原因在于本文采用Matlab平台进行矩阵运算，随着阶数升高，矩阵之间的运算越加耗时。

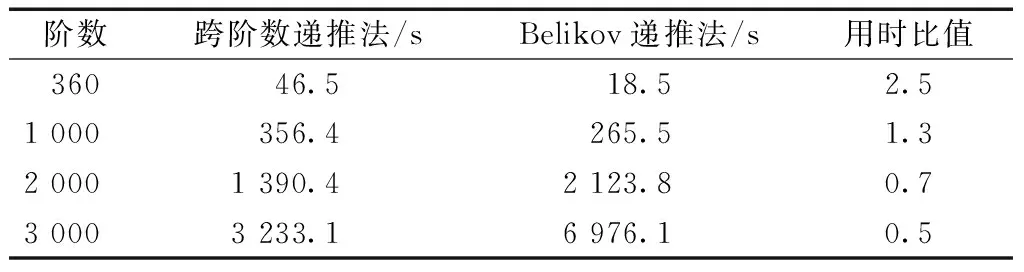
表1 计算用时比较

3 结 论

本文介绍了适用于超高阶缔合勒让德函数计算的跨阶数递推算法和Belikov递推算法，数值计算结果表明，两种方法计算结果的相对精度均优于10-12，跨阶数递推算法在计算速度上优于Belikov递推算法，实用计算时建议使用跨阶次递推算法。

[1] COLMOBO O L.Numerical methods for harmonic analysis on the sphere[J]. OSU Rep 310.Columbus,Ohio:The Ohio state university，1981.

[2] WENZEL G. Ultra-high degree geopotential models GPM98A, B, and C to degree 1800.Paper to the joint meeting of the International Gravity Commission and International Geoid Commission[J],1998，7-12 September,Trieste.

[3] JEKELI C,LEE J K,KWON J H.On the computation and approximation of ultra-high-degree spherical harmonic series[J].J Geod.,2007，81(9):603-615.

[4] FUKUSHIMA T.Numerical computation of spherical harmonics of arbitrary degree and order by extending exponent of floating point numbers[J].J Geod.，2012，86(4)：271-285.

[5] 张传定，许厚泽，吴星.地球重力场调和分析中的“轮胎”问题[C]//大地测量与地球动力学进展.武汉：科学技术出版社，2004：302-314.

[6] 吴星，刘雁雨.多种超高阶缔合勒让德函数计算方法的比较[J].测绘科学技术学报,2006，23(3)：188-191.

[7] 刘缵武，刘世晗，黄欧.超高阶次勒让德函数递推计算中的压缩因子和Horner求和技术[J].测绘学报，2011，40(4)：454-458.

[8] 于锦海，曾艳艳，朱永超，等.超高阶次勒让德函数的跨阶次递推算法[J].地球物理学报，2015，58(3)：748-755.

[9] 王建强，赵国强，朱广彬.常用超高阶次缔合勒让德函数计算方法对比分析[J].大地测量与地球动力学，2009，4(2)：126-130.

[10] PAUL M R.Recurrence relations for integral of associatedlegendre functions[R]. Bulletin Geodesique,1978，53:177-190.

[11] HOLMES S A,FEATHERSTONE W E.A Unified approach to the clenshaw summation and the recursive computation of very high degree and order normalized associated legendre functions[J].J Geod.,2002，76(5):279-299.

[责任编辑：刘文霞]

Calculating the ultra-high-order associated legendre functions by Belikov column method and recursive method between every other order and degreeOU

YANG Mingda1，2，ZHANG Minli2,YU Liang2

(1.Stake Key Laboratory of Geo-information Engineering,Xi’an 710054,China; 2.Technical Division of Surveying and Mapping, Xi’an 710054,China)

Precision construction and rapid calculation of ultra-high-order spherical harmonic gravity field model,depend on the calculation method of the associated legendre functions. On the basis of previous studies,the suitable Belikov column method and recursion method between every other order and degree for ultra-high-order legendre function are introduced. The accuracy of calculations verified results in two ways after are their calculation speeds compared.The result shows that:every associated legendre function calculated by this two algorithms is obtained with absolute accuracy better than 10-12. In low-order, the recursion method between every other order and degree takes time as twice as Belikov column method extrapolation. As the order increasing, the recursion method between every other order and degree shows a significant speed advantage.

Legendre function; recursion function; spherical harmonic analysis

著录：欧阳明达，张敏利，于亮.采用Belikov列推和跨阶次递推方法计算超高阶缔合勒让德函数[J].测绘工程，2017，26(7)：12-15，21.

10.19349/j.cnki.issn1006-7949.2017.07.003

2016-06-24

地理信息工程国家重点实验室开放研究基金资助项目(SKLGIE2015-M-1-2；SKLGIE2016-M-2-2)

欧阳明达(1986-)，男，助理工程师.

P223

A

1006-7949(2017)07-0012-04