生活中的函数问题

文/陈和金 周奕生

智慧数学

生活中的函数问题

文/陈和金 周奕生

责任编辑：王二喜

以生活为背景，考查函数的应用是中考命题的重点.这类问题需要构造函数，运用函数图象和性质解答.常见的问题有如下几种.

一、情景中的函数图象问题

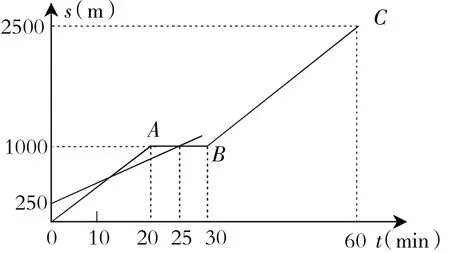
图1

例1（2016年南充卷）小明和爸爸从家步行去公园，爸爸先出发一直匀速前行，小明后出发．家到公园的距离为2500m，图1是小明和爸爸所走的路程s（m）与步行时间t（min）的函数图象．请解答：

（1）直接写出小明所走路程s与时间t的函数关系式；

（2）小明出发多少时间与爸爸第三次相遇？

（3）在速度都不变的情况下，小明希望比爸爸早20min到达公园，则小明在步行过程中停留的时间需作怎样的调整？

解析：（1）小明所走路程s与时间t的图象是折线OABC，因此，求其函数关系式时应按自变量的取值范围分段讨论.

（2）由图象可知：小明第三次与他爸爸相遇是在小明出发30min后，因此，欲知小明与爸爸第三次相遇的时间，需要求出爸爸所走的路程s、时间t的函数图象与s=50t-500的交点．

设s=mt+n，把点（0，250）和（25，1000）代入，得

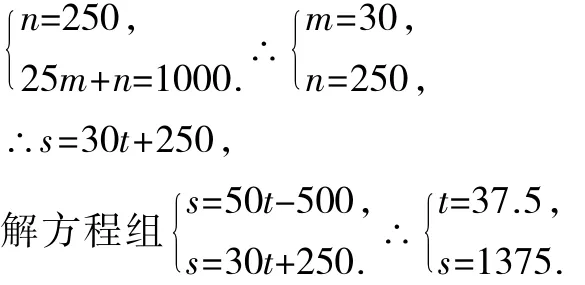
所以小明出发37.5min时，与爸爸第三次相遇.

（3）小明的爸爸到达公园需要的时间：30t+250=2500，解得t=75，

所以小明的爸爸到达公园需要75min．

由图1可知，按原方案小明到达公园需要的时间是60min，75-60=15，他希望比爸爸早20min到达公园，则小明在步行过程中停留的时间需减少5min．

评注：解决情景图象问题的步骤：阅读问题情景→观察函数图象→确定两点坐标→运用待定系数法求值.由于图象是折线，要注意自变量的取值范围，分段解决．

二、售价与销售量的反比例函数问题

例2（2016年德州卷）某中学组织学生到商场参加社会实践活动，他们参与了某种品牌运动鞋的销售工作.已知该运动鞋每双的进价为120元，为寻求合适的销售价格进行了4天的试销，试销情况如表所示：

第1天第2天第3天第4天售价x（元/双）150 200 250 300销售量y（双）40 30 24 20

（1）观察表中数据，x，y满足什么函数关系？请求出这个函数关系式；

（2）若商场计划每天的销售利润为3000元，则每双鞋的售价应定为多少元？

解析：（1）运动鞋每天的售价和销售量的乘积，都等于6000，因此，xy=6000.

（2）每双鞋的利润为（x-120）元．由题意得（x-120）y=3000，

解得x=240．

经检验，x=240是原方程的根．

答：若商场计划每天的销售利润为3000元，则每双鞋的售价应定为240元．

评注：售价越高，销售量越小，需要找到销售量与售价的函数关系．

三、调运方案中的一次函数问题

例3（2016年荆门卷）A城有某种农机30台，B城有该种农机40台，现要将这些农机全部运往C，D两乡，调运任务承包给某运输公司．已知C乡需要农机34台，D乡需要农机36台，从A城往C，D两乡运送农机的费用分别为250元/台和200元/台，从B城往C，D两乡运送农机的费用分别为150元/台和240元/台．

（1）设A城运往C乡该农机x台，运送全部农机的总费用为W元，求W关于x的函数关系式，并写出自变量x的取值范围；

（2）现该运输公司要求运送全部农机的总费用不低于16 460元，则有多少种不同的调运方案？将这些方案设计出来；

（3）现该运输公司决定对A城运往C乡的农机，从运输费中每台减免a元（a≤200）作为优惠，其他费用不变.如何调运，使总费用最少？

解析：（1）由A城运往C乡的农机x台，A城余下的（30-x）台运往D乡，C乡还需（34-x）台，即B城运往C乡的农机为（34-x）台，B城剩下的40-（34-x）台运往D乡，即B城运往D乡（6+x）台．

由题意，可得

W=250x+200（30-x）+150（34-x）+240（6+x）=140x+12 540，

农机数量是非负数，所以x的取值范围为0≤x≤30.

（2）调运方案决定于自变量x的值，故只需要确定x的取值范围．

根据题意，得140x+12 540≥16 460，解得x≥28，

又由（1），得0≤x≤30，所以28≤x≤30，

因为x为整数，所以x=28，29，30，共有3种不同的调运方案，分别是：

从A城调往C乡28台，D乡2台，从B城调往C乡6台，D乡34台；

从A城调往C乡29台，D乡1台，从B城调往C乡5台，D乡35台；

从A城调往C乡30台，D乡0台，从B城调往C乡4台，D乡36台.

（3）根据题意，得W=（250-a）x+200（30-x）+150（34-x）+240（6+x），

整理，得W=（140-a）x+12 540，

①当0＜a＜140时，即140-a＞0，

当x=0时，W最小值=12 540元，

3.5.2 推进区域能源市场建设。加快区域电力市场建设，通过发展辅助服务等方式扩大跨省交易电量，增强区域电力余缺调剂能力，提高区域电网安全性能。充分发挥油气交易平台的辐射作用，支持企业用好国际、国内两个资源，加强地方在能源采购上的话语权。

此时从A城调往C乡0台，调往D乡30台，从B城调往C乡34台，调往D乡6台；

②当a=140时，W=12 540元，各种方案的费用一样多；

③当140＜a≤200时，140-a＜0，

当x=30时，W最小=16 740-30a，

此时从A乡调往C乡30台，D乡0台，从B乡调往C乡4台，D乡36台．

评注：方案设计常常涉及利润最大（成本最小）问题，需要构造利润（成本）与变量之间的一次函数，利用一次函数的增减性及自变量的取值范围确定最大值（最小值）．

四、营销利润中的二次函数问题

例4（2016年潍坊卷）旅游公司在景区内配置了50辆观光车供游客租赁使用，假定每辆观光车一天内最多只能出租一次，且每辆车的日租金x（元）是5的倍数．每天的营运规律如下：当x不超过100元时，观光车能全部租出；当x超过100元时，每辆车的日租金每增加5元，租出去的观光车就会减少1辆．已知所有观光车每天的管理费是1100元．

（2）当每辆车的日租金为多少元时，每天的净收入最多？

解析：（1）每天的净收入=出租车的总收入-管理费，总收入=每辆车的日租金×租出车的数量．50辆观光车全部租出的总收入为50x，净收入为50x-1100（元）．

由每天的净收入为正，得50x-1100＞0，解得x＞22，

又x是5的倍数，所以每辆车的日租金至少为25元.

（2）设每天的净收入为y元，由题意可知y与x之间是分段函数，需要分段求出函数的最大值，再比较得出答案．

当0＜x≤100时，50辆观光车能全部租出，所以y1＝50x-1100，

y1随x的增大而增大，所以当x=100时，y1取最大值，最大值为50×100-1100=3900；

当x=175时，y2取最大值，最大值为5025．

因为5025＞3900，故当每辆车的日租金为175元时，每天的净收入最多，为5025元．

评注：营销中的利润决定于销售的单价和销量，单价提高，销售量就会减少，利润与销售单价一般是二次函数关系.建立利润与销售单价的二次函数关系，利用二次函数的性质求解．