数形结合思想的应用

文/李培华

数形结合思想的应用

文/李培华

责任编辑：王二喜

数形结合是解决数学问题常见的方法.它是根据题设和结论之间的内在关系，既分析其数量关系，又揭示其几何意义，使数量关系和几何图形巧妙地结合起来，从而发现解决问题的思路.请看下面的例子.

一、在数与式中的应用

例1如图1，边长为a的正方形中有一个边长为b的小正方形，若将图1的阴影部分拼成一个长方形，如图2，比较图1和图2的阴影部分的面积，你能得到的公式是______.

解：图1中阴影部分的面积为：a2-b2；图2中阴影部分的面积为：（a+b）（a-b）.它们的面积相等.

故答案为a2-b2=（a+b）（a-b）.

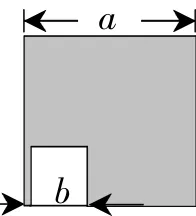
图1

图2

二、在平面直角坐标系中的应用

例2在平面直角坐标系中，已知点E（-4，2），F（-2，-2），以原点O为位似中心，相似比为，把△EFO缩小，则点E的对应点E′的坐标是（ ）

A.（-2，1）. B.（-8，4）.

C.（-8，4）或（8，-4）. D.（-2，1）或（2，-1）.

解：由图3可知,点E的对应点的坐标是（-2，1）或（2，-1）．选D.

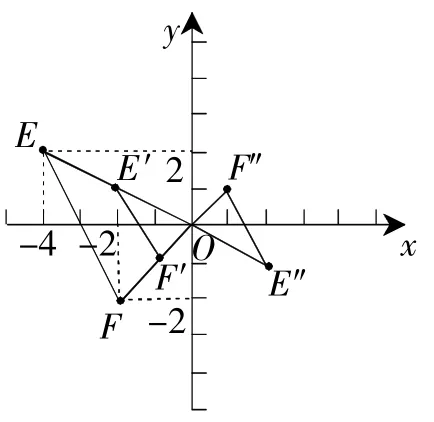
图3

三、在统计中的应用

例3某棵果树前x年的总产量y与x之间的关系如图4所示，从目前记录的结果看，前x年的年平均产量最高，则x的值为（ ）

A．3． B．5. C．7. D．9.

解：设图4中的对应点为P（x，y），则前x年的年平均产量即为直线OP的斜率，当x=7时，直线OP的斜率最大，即前7年的年平均产量最高.故选C.

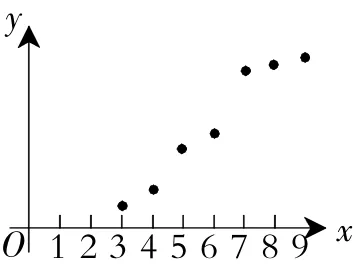
图4

四、在函数中的应用

例4图5是我国古代计时器“漏壶”的示意图，在壶内盛一定量的水，水从壶底的小孔漏出．壶壁内画有刻度，人们根据壶中水面的位置计时.用x表示时间，y表示壶底到水面的高度，则y与x的图象是（ ）.

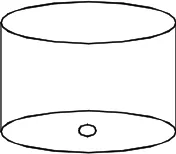
图5

解：壶内盛一定量的水，y的初始高度大于0，可以排除A，B；漏水的速度不变，水位逐渐下降，可以排除D选项.选C.

五、在不等式中的应用

例5已知一次函数y=x-2，当y＞0时，x的取值范围在数轴上表示正确的是（ ）

解：∵y＞0，∴x-2＞0，解得x＞2.选B.

六、在方程中的应用

例6二次函数y=-x2+2x+k的部分图象如图6所示，则关于x的一元二次方程-x2+2x+k=0的一个解x1=3，另一个解x2=（ ）

A.1. B.-1. C.-2. D.0.

解：x1+x2==2，而x1=3，∴x2=-1.选B.

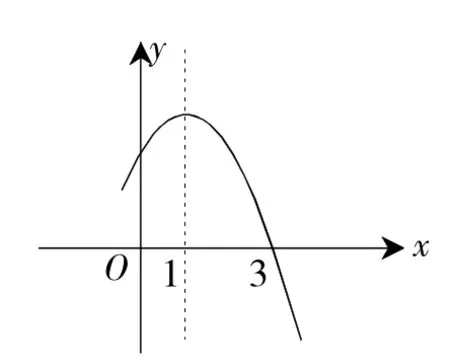
图6